[数据结构与算法]二叉树知识之6赫夫曼树

赫夫曼树的知识和代码实现

1什么是赫夫曼树

给定n个权值作为n个叶子节点，构造成一棵二叉树，若树的带权路径长度最小（wpl）则称此树为最优二叉树。即赫夫曼树。

2创建赫夫曼树的步骤

给定一个无序的数组，进行赫夫曼树的创建步骤

1. 先将数组从小到大进行排序。
   

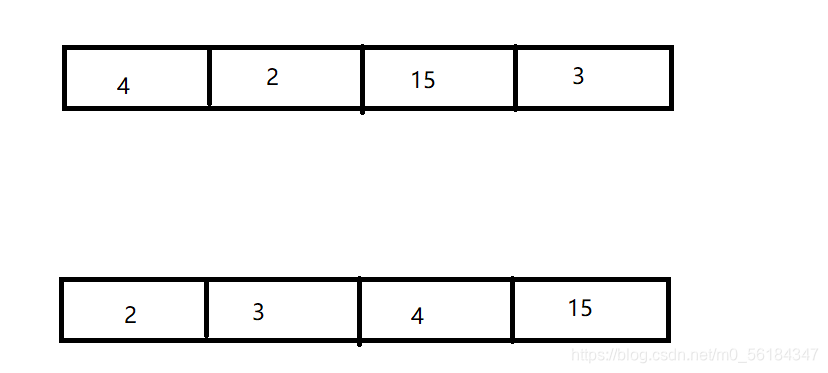
2. 取出根节点权值最小的两个树
   

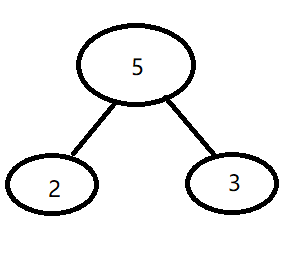
3. 组成一颗新的树，该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
   

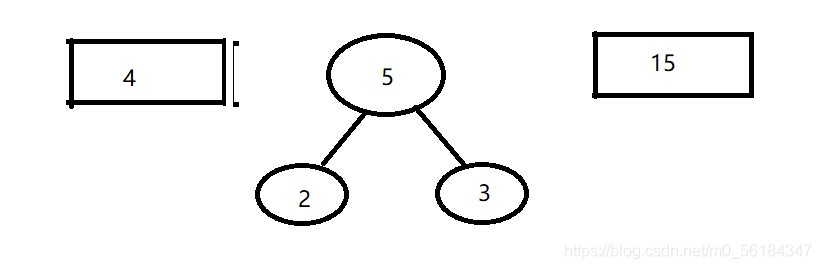
4. 再将这两颗新的二叉树，以根节点的权值大小再次排序，

5. 重复步骤2
   
   

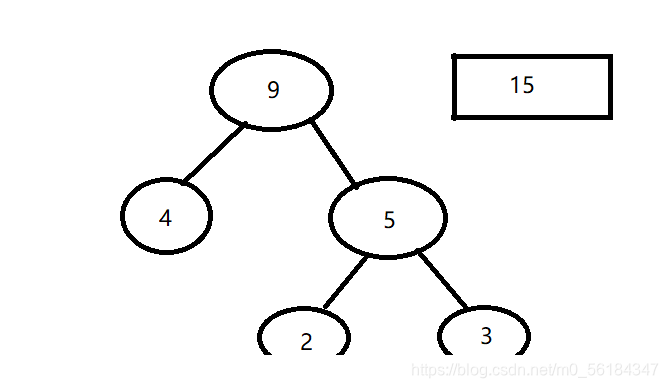
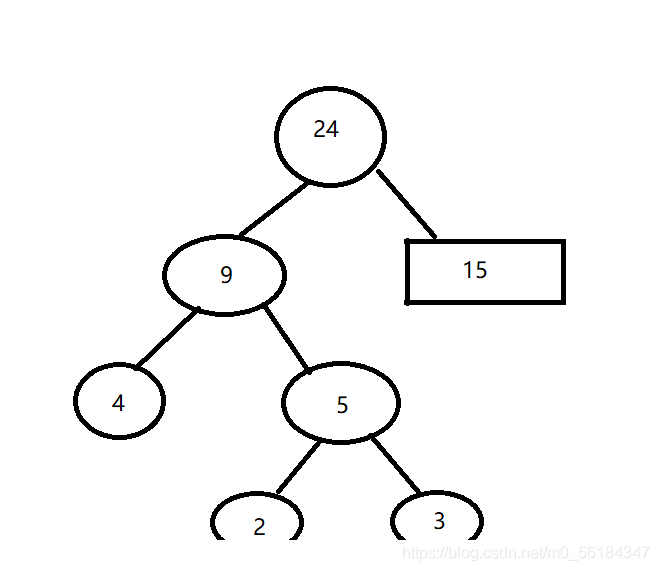
即可得到一颗赫夫曼树！（wpl值最小的树）

3赫夫曼树的代码实现

package com.njupt.binaryTree;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

/**
 * Creat with IntelliJ IDEA
 *
 * @Auther:倔强的加瓦
 * @Date:2021/07/28/20:53
 * @Description:
 */
public class HuffmanTree {
    public static void main(String[] args) {

        int[] arr = {13, 7, 8, 3, 29, 6, 1};
        NodePoint1 root = creatTree(arr);
        preOrder(root);

    }

    public static void preOrder(NodePoint1 root) {
        if (root != null) {
            root.preOrder();
        } else {
            System.out.println("此树为空");
        }
    }

    public static NodePoint1 creatTree(int[] arr) {
        List<NodePoint1> nodePoints = new ArrayList<NodePoint1>();
        //遍历数组，将数组中的数和每一个节点进行绑定，然后添加到链表中。
        for (int i = 0; i < arr.length; i++) {
            nodePoints.add(new NodePoint1(arr[i]));
        }
        //工具类，从小到大排序插入！
        //System.out.println(nodePoints);
        while (nodePoints.size() > 1) {
            //先对节点数组进行排序
            Collections.sort(nodePoints);
            //第一步，取出权值最小的两个节点
            NodePoint1 left = nodePoints.get(0);
            NodePoint1 right = nodePoints.get(1);
            //第二步。相加，然后将结果加入到链表中
            NodePoint1 parent = new NodePoint1(left.no + right.no);
            //将父亲节点连上，创建好二叉树
            parent.left = left;
            parent.right = right;
            //把相加之后的子节点移除
            nodePoints.remove(left);
            nodePoints.remove(right);
            //把父节点添加进去
            nodePoints.add(parent);
        }
        //因为里面只剩下这一个头节点了。
        return nodePoints.get(0);
    }
}

class NodePoint1 implements Comparable<NodePoint1> {
    int no;
    NodePoint1 left;
    NodePoint1 right;

    public NodePoint1(int no) {
        this.no = no;
    }

    @Override
    public String toString() {
        return "NodePoint1{" +
                "no=" + no +
                '}';
    }

    @Override
    public int compareTo(NodePoint1 node) {
        //从小到大排序
        return this.no - node.no;
    }

    public void preOrder() {
        System.out.println(this.no);
        if (this.left != null) {
            this.left.preOrder();
        }
        if (this.right != null) {
            this.right.preOrder();
        }
    }
}

测试结果;对创建好的哈夫曼树进行前序遍历。

24
9
4
5
2
3
15

Process finished with exit code 0