6.1.算法原理
几何角度,对于线性可分的数据集,SVM就是找一个离正负样本都最远的超平面,相比于感知机,其解是唯一的,(感知机只要能分开正负样本即可),且泛化性更好。
现实任务中,线性不可分的情形最常见的,因此要允许支持向量机犯错。
6.2 超平面
一维空间超平面是个点
二维空间是个线
三维空间是个面
n维空间

不唯一是因为w和b都可等比例缩放。
和法向量同向的那一半是正平面(带进去>0)
证明上图的距离公式

6.3 几何间隔
对于线性可分的数据集来说,当正确分类时,几何间隔等价于颠倒超平面的距离.

数据集X关于超平面的几何间隔为数据集中所有样本点的几何间隔的最小值。
6.3 支持向量机
希望几何间隔达到最大
模型:阶跃函数

所谓的越靠近中央越大是指有很多可以把正负样例分开的超平面,如果都平行的话中间的超平面几何间隔比较大。
策略:转换成带约束的优化问题

无法解出最优解,因为若有最优解w和b,同步放大kb可以得到无数最优解,但最优解只有一个。需要固定分子或分母。


对于优化目标函数是凸函数,约束集合是凸集,该问题为凸优化问题。海塞矩阵可证凸函数。


拉格朗日对偶问题

拉格朗日对偶问题恒为凸优化问题
KTT条件(5个)


对偶问题本质上是最大化问题
什么是对偶问题:原来是min(max),转换成max(min),且原来的条件转换成变量,原来的变
量转换成条件,还要满足KTT条件。转换的原因是原来的情况不好求解,这样比较好求解。


6.4 软间隔与支持向量回归
6.4.1 算法原理
在现实任务中,线性不可分的情形才是最常见的,因此需要允许支持向量机犯错(异常样本)
6.4.2 软间隔

优化目标+损失(约束条件)


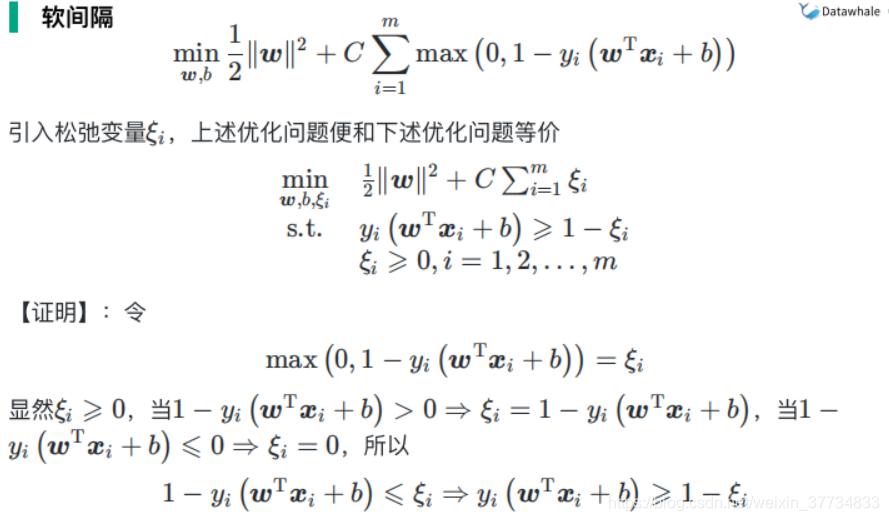
6.4.3 支持向量回归(SVR)
一条线变成一条带子


