[数据结构与算法]leetcode(33)_863_medium_二叉树中所有距离为 K 的结点_python

二叉树中所有距离为 K 的结点

题目描述：
给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。
返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

示例 ：

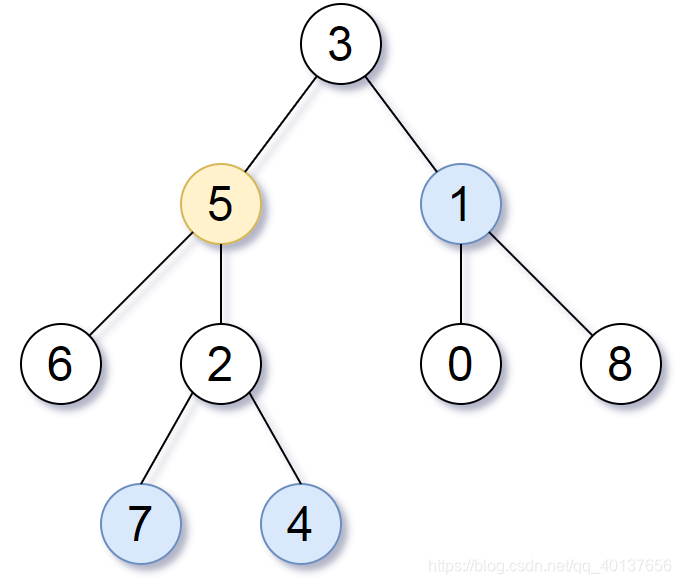
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：所求结点为与目标结点（值为 5）距离为 2 的结点，值分别为 7，4，以及 1
注意，输入的 “root” 和 “target” 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。
提示：

• 给定的树是非空的。
• 树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
• 目标结点 target 是树上的结点。
• 0 <= K <= 1000.

解法

1. 从target开始寻找距离为 K 的结点时，有两个方向：第一个是往其孩子结点走，也就是往下走 K 步即可；第二个是往父节点记作parent走，我们不妨假设target是parent的左孩子，在到达parent后，由于不能原路返回，所以要么继续往上再找parent的父节点，要么沿着parent的另一侧，也就是从parent的右孩子不断往下走。
2. 第一个方向是非常好实现的，我们需要记录走了多少步，满 K 步后把对应的结点值记录下来即可。
3. 第二个方向也不麻烦，到达parent后再往右孩子的方向走，就相当于从parent的右侧再走 K - 1 步；如果继续往上找到parent的父节点，那就是再走 K - 2 步。所以我们在确定target的位置时，需要把途径的结点记录下来。同时我们也要注意在往父节点走的时候，不能原路返回，所以需要判断孩子在父节点的哪一侧，确定好之后往另一侧走即可。

代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
        path, res = [], []  # 找到 target 途经的结点集合，距离为 k 的结点集合
        self.findTarget(root, target, path)  # 寻找 target
        for i in range(min(k + 1, len(path))):  # 如果 k 比较小，较远的父亲节点并不会达到
            if i == 0:  # 起点为 target，往下走 k 步
                self.findDistanceKInChild(path[i], k - i, res)
            elif i == k:  # 此时该节点就与 target 距离 k 步，不用再往下走了
                res.append(path[i].val)
            elif path[i - 1] == path[i].right:  # 如果 path[i - 1] 在 path[i] 的右侧，那只能往 path[i] 的左侧走
                self.findDistanceKInChild(path[i].left, k - i - 1, res)
            else:  # 如果 path[i - 1] 在 path[i] 的左侧，那只能往 path[i] 的右侧走
                self.findDistanceKInChild(path[i].right, k - i - 1, res)
        return res

    def findTarget(self, root: TreeNode, target: TreeNode, path):
        if not root:
            return False
        # 如果该节点就是 target；或者在左侧找到；或者在右侧找到，就说明该节点处于路径上，记录下来
        if root == target or self.findTarget(root.left, target, path) or self.findTarget(root.right, target, path):
            path.append(root)
            return True
        return False
    
    def findDistanceKInChild(self, root, k, res):
        if not root:
            return
        if k == 0:  # 走了 k 步，记录结果
            res.append(root.val)
            return
        self.findDistanceKInChild(root.left, k - 1, res)
        self.findDistanceKInChild(root.right, k - 1, res)
        return
      

测试结果

执行用时：44 ms, 在所有 Python3 提交中击败了 74.23% 的用户
内存消耗：15.1 MB, 在所有 Python3 提交中击败了 94.68% 的用户

说明

算法题来源：力扣(LeetCode)