性能:

1.冒泡排序
每次遍历排序都找出一个最大值放在后面 就像冒泡一样 应用了交换的思想
[3,?9,?-1, 10, 20]
第1次遍历排序:
[3, -1, 9, 10, 20]
第2次遍历排序:
[-1, 3, 9, 10, 20]
第3次遍历排序:
[-1, 3, 9, 10, 20]
第4次遍历排序:
[-1, 3, 9, 10, 20]
最终排序结果:
[-1, 3, 9, 10, 20]
*所以5个数组进行4次遍历排序就可
*根据上面的遍历我们还发现第三次遍历数组已经有序,无需进行第四次遍历,所以我们可以对这点进行优化 。? 也就是如果经历一次遍历排序一次交换也没发生,那么我们就认为这个数组已经有序,直接retuen.
1.1代码实现:
/**
* 冒泡排序
* @param arr 进行排序的数组
* @return 排好序的数组
*/
public static int[] bubbleSort(int[] arr) {
int temp = 0;
int count = 0;
for (int i = arr.length-1; i > 0; i--) {
count = 0;
//每次循环都遍历出了一个最大的放在数组的后面
for (int j = 0; j < i ; j++) {
//如果比后一个元素大则进行交换
if(arr[j] > arr[j+1]) {
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
//记录进行交换的次数
count++;
}
}
// System.out.println("第" + (arr.length-i) +"次排序:");
// System.out.println(Arrays.toString(arr));
//说明已经有序了 无须在排
if(count == 0) {
return arr;
}
}
return arr;
}1.2测试排序十万个随机数所需要的时间:
//创建随机数组
int[] testArr = new int[100000];
for (int i = 0; i < testArr.length; i++) {
//生成[0,8000]间的随机数
testArr[i] = (int) (Math.random()*8000000);
}
//开始时间
Date dataBegin = new Date();
//冒泡排序
sort.bubbleSort(testArr);
//结束时间
Date dataEnd = new Date();
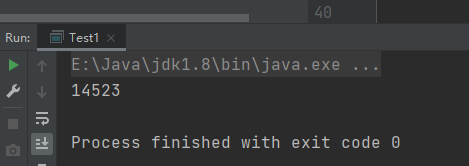
System.out.println(dataEnd.getTime()-dataBegin.getTime());结果:14523ms
?
2.简单选择排序
每次遍历排序都选择一个最小值 然后与最前面的数进行交换? 与冒泡排序不同 只交换一次
[3, 9, -1, 10, 20]
第1次遍历排序:
[-1, 9, 3, 10, 20]
第2次遍历排序:
[-1, 3, 9, 10, 20]
第3次遍历排序:
[-1, 3, 9, 10, 20]
第4次遍历排序:
[-1, 3, 9, 10, 20]
最终排序结果:
[-1, 3, 9, 10, 20]
2.1代码实现
/**
* 选择排序
* @param arr 进行排序的数组
* @return 排好序的数组
*/
public static int[] selectSort(int[] arr) {
int temp = 0;
//最小值的下标
int min = 0;
for (int i = 0; i < arr.length - 1; i++) {
//先假设最小的数是arr[i]
min = i;
//遍历找到最小的那个
for (int j = i + 1; j < arr.length; j++) {
//如果发现arr[j] 比 arr[min]小 则令min = j
if(arr[j] < arr[min]) {
min = j;
}
}
//将的到的最小值与arr[i]进行交换
if (min != i) {
temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
// System.out.println("第" + (i+1) +"次排序:");
// System.out.println(Arrays.toString(arr));
}
return arr;
}2.2测试排序十万个随机数所需要的时间:
//创建随机数组
int[] testArr = new int[100000];
for (int i = 0; i < testArr.length; i++) {
//生成[0,8000]间的随机数
testArr[i] = (int) (Math.random()*8000000);
}
//开始时间
Date dataBegin = new Date();
//选择排序
sort.selectSort(testArr);
//结束时间
Date dataEnd = new Date();
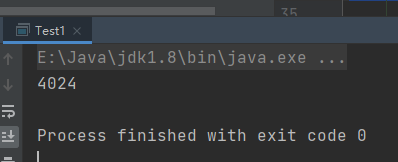
System.out.println(dataEnd.getTime()-dataBegin.getTime());结果:4024ms
3.直接插入排序
先将要排序数组中第一个数当作以已排序好的数组,然后依次遍历剩下的数 按顺序插入已排序好的数组。全部遍历一遍后则得到一个排序好的数组。
[3, 9, -1, 10, 20]
第1次遍历排序:
[3, 9, -1, 10, 20]
第2次遍历排序:
[-1, 3, 9, 10, 20]
第3次遍历排序:
[-1, 3, 9, 10, 20]
第4次遍历排序:
[-1, 3, 9, 10, 20]
最终排序结果:
[-1, 3, 9, 10, 20]
3.1代码实现:
/**
* 插入排序
* @param arr 进行排序的数组
* @return 排好序的数组
*/
public static int[] insertSort(int[] arr) {
//要插入的值
int insertValue;
//插入的下标
int insertIndex;
for (int i = 1; i < arr.length; i++) {
insertValue = arr[i];
//先假设为已经 排好序的数组中最后一个
insertIndex = i - 1;
//如果下标小于0了说明已经跟 已排好序的数组全部做过了比较
//如果要插入的那个值 小于 已排好序的数组中最后一个 九将这个数后移以为 然后在往前遍历 依此比较
//知道找到一个比要插入值小的 则该点就是要插入的点
//如果一次while循环也没进入 则说明要插入的这个值比 已排好序的数组中所有的都要大
while (insertIndex >= 0 && insertValue < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
//将值插入
arr[insertIndex + 1] = insertValue;
System.out.println("第" + i +"次遍历排序:");
System.out.println(Arrays.toString(arr));
}
return arr;
}3.2测试排序十万个随机数所需要的时间:
//创建随机数组
int[] testArr = new int[100000];
for (int i = 0; i < testArr.length; i++) {
//生成[0,8000]间的随机数
testArr[i] = (int) (Math.random()*8000000);
}
//开始时间
Date dataBegin = new Date();
//插入排序
sort.insertSort(testArr);
//结束时间
Date dataEnd = new Date();
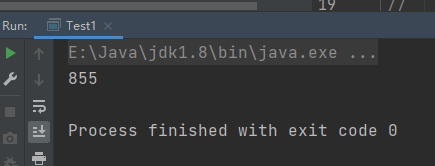
System.out.println(dataEnd.getTime()-dataBegin.getTime());结果:855
?
希尔排序
快速排序
归并排序
基数排序