[数据结构与算法]P1002 [NOIP2002 普及组] 过河卒

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

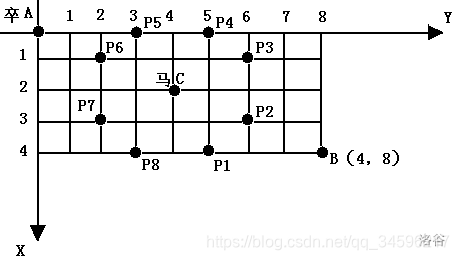
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入
6 6 3 3
输出
6

方法：动态规划
递归式： a[i][j] = a[i - 1][j] + a[i][j - 1];

#include <iostream>
#include <cstring>

#define max 1000

using namespace std;

int main()
{
    int bx, by, cx, cy;
    cin >> bx >> by >> cx >> cy;
    long long a[max][max];              //long long 数据超出int
    int cony[8] = {-2, -1, 1, 2, 2, 1, -1, -2};		//计算控制点
    int conx[8] = {-1, -2, -2, -1, 1, 2, 2, 1};
    int isControl[max][max];  // 标记是不是马的控制点
    memset(isControl, 0, sizeof(isControl));
    isControl[cx][cy] = 1;
    
    for (int i = 0; i <= 7; ++i)			//计算控制点，是的话标记点为1
    {
        if (cx + conx[i] >= 0 && cx + conx[i] <= bx && cy + cony[i] >= 0 && cy + cony[i] <= by)
        {
            isControl[cx + conx[i]][cy + cony[i]] = 1;
        }
    }

    int i = 0;					//初始化边界
    while (!isControl[i][0] && i <= bx)
    {
        a[i++][0] = 1;
    }
    i = 0;
    while (!isControl[0][i] && i <= by)
    {
        a[0][i++] = 1;
    }

    for (i = 1; i <= bx; ++i)			//dp计算
    {
        for (int j = 1; j <= by; ++j)
        {
            if (isControl[i][j])
                a[i][j] = 0;
            else
            {
                a[i][j] = a[i - 1][j] + a[i][j - 1];
            }
        }
    }
    cout << a[bx][by]<<endl;
    return 0;
}