数据分析之决策树（下）

CART算法

cart只支持二叉树，由于cart的特殊性，cart既可以作为分类树也可以作为回归树

cart和c4.5算法类似，只是属性选择的指标采用的是基尼系数。

基尼系数的计算公式：

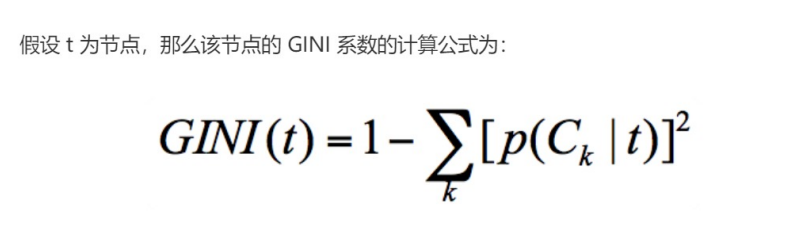
怎么计算呢，举个例子吧

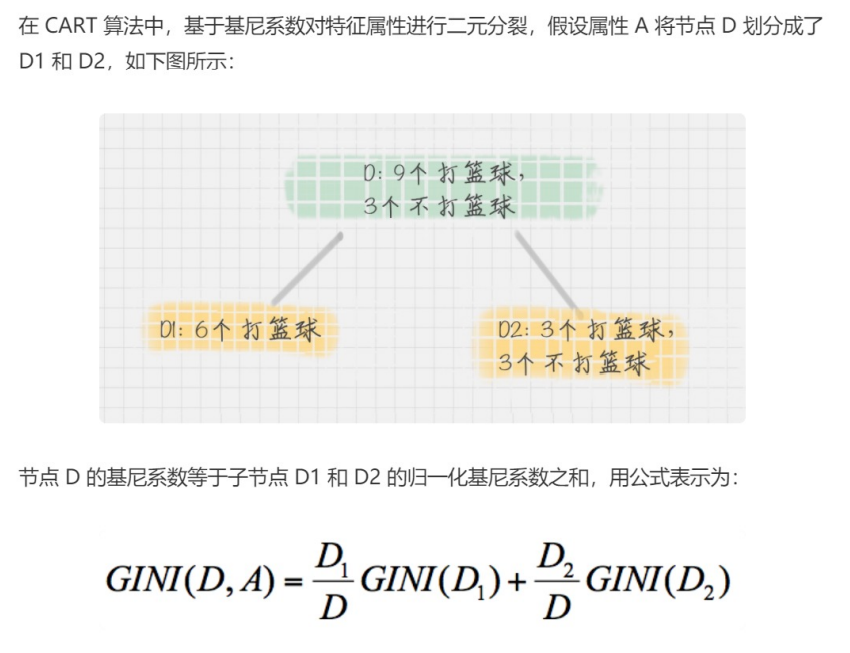
集合1，6个都去打篮球

集合2，3个去打篮球，3个不去打篮球

集合1的基尼系数p(Ck|t) = 1-1 = 0

集合2的基尼系数p(Ck|t) = 1-(0.5 * 0.5+0.5 * 0.5) = 0.5

在这里p(Ck|t)表示节点t属于类别Ck的概率，节点t的基尼系数为1减去各类别Ck概率的平方和，基尼系数越小越稳定

在python中，我们要怎么写我们的cart决策树呢

from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris

#准备数据集
iris = load_iris()
#获取特征集和分类标识
features = iris.data
labels = iris.target
#随机抽取33%的数据作为测试集，其余为训练集
train_features,test_features,train_labels,test_labels = train_test_split(features,labels)
#创建cart分类树
clf = DecisionTreeClassifier(criterion='gini')
#拟合构造cart分类树
clf = clf.fit(train_features,train_labels)
#用cart分类树做预测
test_predict = clf.predict(test_features)
#预测结果与测试集结果作对比
score = accuracy_score(test_labels,test_predict)
print('cart分类树准确率 %.4lf' % score)

cart回归树

cart回归树和分类树的做法是一样的，只是回归树要得到的结果是连续值，而且评判"不纯度"的指标不同。怎么计算不纯度呢，主要是根据样本的离散程度来评价”不纯度“，离散程度的计算方式是计算差值的绝对值或者方差

这两种节点划分的标准分别对应着两种目标函数最优化的标准，既用最小绝对偏差（LDA）或者使用最小乘偏差（LSD）。这两种方式都可以让我们找到节点划分的方法，通常使用最小二乘偏差的情况更常见一些，举个栗子，使用cart回归树波士顿房价进行预测

from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
from sklearn.tree import DecisionTreeRegressor


#准备数据集
boston = load_boston()
#探索数据
print(boston.feature_names)
#获取特征集和房价
features = boston.data
prices = boston.target
#随机抽取33%的数据作为测试集，其余为训练集
train_features,test_features,train_price,test_price = train_test_split(features,prices)
#创建cart回归树
dtr = DecisionTreeRegressor()
#拟合构造cart回归树
dtr.fit(train_features,train_price)
#预测测试集中的房价
predict_price = dtr.predict(test_features)
#测试集的结果评价
print('回归树二乘偏差均值:',mean_squared_error(test_price,predict_price))
print('回归树绝对值偏差均值:',mean_absolute_error(test_price,predict_price))