日撸代码300行の学习笔记3:树与二叉树
前言
??本文是关于日撸代码300行 link的学习笔记。
??Time is all u need.
day21 二叉树的深度遍历的递归实现
??将繁琐的初始化构造单独写个static方法。
??递归中,先给出base case,再在后面分情况递归。
??可以看到,三种遍历通过递归的实现是非常简洁的。
package dataStructure.tree;
/**
* Binary tree with char type elements.
*
* @author Fan Min minfanphd@163.com.
* @learner CatInCoffee
*/
public class BinaryCharTree {
char value;
BinaryCharTree leftChild;
BinaryCharTree rightChild;
public BinaryCharTree(char paraValue) {
value = paraValue;
leftChild = null;
rightChild = null;
}// Of the first constructor
// Pre-order visit.
public void preOrderVisit() {
System.out.print("" + value + " ");
if (leftChild != null) {
leftChild.preOrderVisit();
} // Of if
if (rightChild != null) {
rightChild.preOrderVisit();
} // Of if
}// Of preOrderVisit
// In-order visit.
public void inOrderVisit() {
if (leftChild != null) {
leftChild.inOrderVisit();
} // Of if
System.out.print("" + value + " ");
if (rightChild != null) {
rightChild.inOrderVisit();
} // Of if
}// Of inOrderVisit
// Post-order visit.
public void postOrderVisit() {
if (leftChild != null) {
leftChild.postOrderVisit();
} // Of if
if (rightChild != null) {
rightChild.postOrderVisit();
} // Of if
System.out.print("" + value + " ");
}// Of postOrderVisit
/**
* Get the height of the binary tree.
*
* @return The height. It is 0 if there is only one node, i.e., the root.
*/
public int getHeight() {
// It's the base case of the recursion, which means the recursion reaches to a leaf.
if ((leftChild == null) && (rightChild == null)) {
return 0;
} // Of if
// The height of the left child.
int tempLeftHeight = 0;
if (leftChild != null) {
tempLeftHeight = leftChild.getHeight();
} // Of if
// The height of the right child.
int tempRightHeight = 0;
if (rightChild != null) {
tempRightHeight = rightChild.getHeight();
} // Of if
// The depth should be increased by 1.
// if (tempLeftDepth >= tempRightDepth) {
// return tempLeftDepth + 1;
// } else {
// return tempRightDepth + 1;
// } // Of if
return Math.max(tempLeftHeight, tempRightHeight) + 1;
}// Of getHeight
/**
* Get the total number of nodes.
*
* @return The total number of nodes.
*/
public int getNumNodes() {
if ((leftChild == null) && (rightChild == null)) {
return 1;
} // Of if
// The number of nodes of the left child.
int tempLeftNodes = 0;
if (leftChild != null) {
tempLeftNodes = leftChild.getNumNodes();
} // Of if
// The number of nodes of the right child.
int tempRightNodes = 0;
if (rightChild != null) {
tempRightNodes = rightChild.getNumNodes();
} // Of if
// The total number of nodes.
return tempLeftNodes + tempRightNodes + 1;
}// Of getNumNodes
public static void main(String args[]) {
BinaryCharTree tempTree = manualConstructTree();
System.out.println("Preorder visit:");
tempTree.preOrderVisit();
System.out.println("\r\nIn-order visit:");
tempTree.inOrderVisit();
System.out.println("\r\nPost-order visit:");
tempTree.postOrderVisit();
System.out.println("\r\n\r\nThe height of the tree is: " + tempTree.getHeight());
System.out.println("The number of nodes is: " + tempTree.getNumNodes());
}// Of main
public static BinaryCharTree manualConstructTree() {
// Step 1. Construct a tree with only one node.
BinaryCharTree resultTree = new BinaryCharTree('a');
// Step 2. Construct all nodes. The first node is the root.
// BinaryCharTreeNode tempTreeA = resultTree.root;
BinaryCharTree tempTreeB = new BinaryCharTree('b');
BinaryCharTree tempTreeC = new BinaryCharTree('c');
BinaryCharTree tempTreeD = new BinaryCharTree('d');
BinaryCharTree tempTreeE = new BinaryCharTree('e');
BinaryCharTree tempTreeF = new BinaryCharTree('f');
BinaryCharTree tempTreeG = new BinaryCharTree('g');
// Step 3. Link all nodes.
resultTree.leftChild = tempTreeB;
resultTree.rightChild = tempTreeC;
tempTreeB.rightChild = tempTreeD;
tempTreeC.leftChild = tempTreeE;
tempTreeD.leftChild = tempTreeF;
tempTreeD.rightChild = tempTreeG;
return resultTree;
}// Of manualConstructTree
}// of class BinaryCharTree
??结果:
Preorder visit:
a b d f g c e
In-order visit:
b f d g a e c
Post-order visit:
f g d b e c a
The height of the tree is: 3
The number of nodes is: 7
day22 二叉树的存储
??二叉树的存储并非一个简单的问题,引用 (指针) 是无法存储到文件里面的。
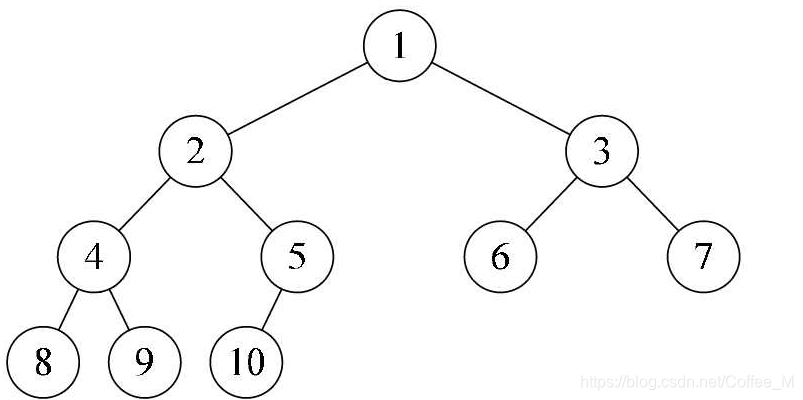
??从完全满二叉树的角度广度优先遍历的角度来考虑这个问题:每个节点都有一个value及其在二叉树中的位置。令根节点的位置为 0,则第 2 层节点的位置依次为 1 至 2;第 3 层节点的位置依次为 3 至 6。以此类推。
??先补充一些国内外不同的定义,经过对比,个人将沿用国外的定义。
完全二叉树 Complete Binary Tree:(国内外相同)
??一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果某编号的结点与完美二叉树中编号相同的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
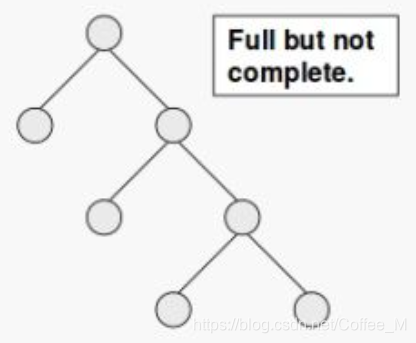
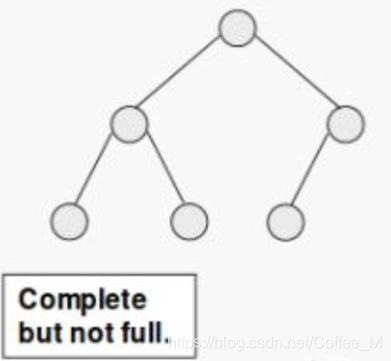
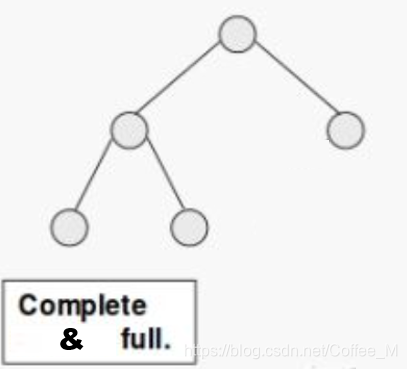
满二叉树 Full Binary Tree: (国内是完美平衡树,国外是节点度为0或2的一种性质)
??a binary tree T is full if each node is either a leaf or possesses exactly two childnodes.
 |  |  |
|---|
完美二叉树 Perfect Binary Tree:
??Every node except the leaf nodes have two children and every level (last level too) is completely filled.

??也有称perfectly balanced tree,理想平衡树。
??完美二叉树,显然是完全满二叉树。
??把昨天那个例子所对应的二叉树画出来,我们有两种方法:
??1:空使用 0 来表示,用一个向量来存储,则有:
??优点:仅需要一个向量,简单粗暴。
??缺点:对于实际的二叉树,很多子树为空,导致大量的 0 值。
??2:使用压缩存储方式,即将节点的位置和值均存储。那么,昨天例子可表示为两个向量:
??由于递归程序涉及变量的作用域问题,我们需要使用层次遍历(也叫层序遍历,level order traversal)的方式,以获得以上的几个向量。层序遍历需要用到队列,而不是递归默认的栈。
??下面将队列的代码再写一遍,和之前的CircleIntQueue类似,但这次装的是对象 (的引用)。
package dataStructure.queue;
/**
* Circle Object queue.
*
* @author Fan Min minfanphd@163.com.
* @learner CatInCoffee.
*/
public class CircleObjectQueue {
/**
* The total space. And one space can never be used.
*/
public static final int TOTAL_SPACE = 10;
/**
* The data.
*/
Object[] data;
/**
* The index of the head.
*/
int head;
/**
* The index of the tail.
*/
int tail;
public CircleObjectQueue() {
data = new Object[TOTAL_SPACE];
head = 0;
tail = 0;
}// Of the first constructor
/**
* Enqueue.
*
* @param paraValue The value of the new node.
*/
public void enqueue(Object paraValue) {
if ((tail + 1) % TOTAL_SPACE == head) {
System.out.println("\n\tQueue full.");
return;
} // Of if
data[tail % TOTAL_SPACE] = paraValue;
tail++;
}// Of enqueue
/**
*********************
* Dequeue.
*
* @return The value at the head.
*********************
*/
public Object dequeue() {
if (head == tail) {
// System.out.println("No element in the queue");
return null;
} // Of if
Object resultValue = data[head % TOTAL_SPACE];
head++;
return resultValue;
}// Of dequeue
/**
* Overrides the method claimed in Object, the superclass of any class.
*/
public String toString() {
String resultString = "";
if (head == tail) {
return "empty";
} // Of if
for (int i = head; i < tail; i++) {
resultString += data[i % TOTAL_SPACE] + ", ";
} // Of for i
return resultString;
}// Of toString
public boolean isEmpty() {
return head == tail;
}// of isEmpty()
public int size() {
return tail - head;
}// of size()
public static void main(String args[]) {
CircleObjectQueue tempQueue = new CircleObjectQueue();
System.out.println("Initialized, the list is: " + tempQueue);
for (int i = 0; i < 5; i++) {
tempQueue.enqueue(i);
} // Of for i
System.out.println("Enqueue, the queue is: " + tempQueue);
int tempValue = (Integer)tempQueue.dequeue();
System.out.println("Dequeue " + tempValue + ", the queue is: " + tempQueue);
tempValue = (Integer)tempQueue.dequeue();
System.out.println("Dequeue " + tempValue + ", the queue is: " + tempQueue);
System.out.println();
for (int i = 0; i < 7; i++) {
tempQueue.enqueue(i + 5);
System.out.println("Enqueue, the queue is: " + tempQueue);
} // Of for i
System.out.println();
for (int i = 0; i < 9; i++) {
tempQueue.dequeue();
} // Of for i
System.out.println("Dequeue 9 elements , and the queue is: " + tempQueue);
System.out.println();
tempQueue.dequeue();
System.out.println("Dequeue, the queue is: " + tempQueue);
tempQueue.enqueue(10);
System.out.println("Enqueue, the queue is: " + tempQueue);
}// Of main
}// of class CircleObjectQueue
??结果:
Initialized, the list is: empty
Enqueue, the queue is: 0, 1, 2, 3, 4,
Dequeue 0, the queue is: 1, 2, 3, 4,
Dequeue 1, the queue is: 2, 3, 4,
Enqueue, the queue is: 2, 3, 4, 5,
Enqueue, the queue is: 2, 3, 4, 5, 6,
Enqueue, the queue is: 2, 3, 4, 5, 6, 7,
Enqueue, the queue is: 2, 3, 4, 5, 6, 7, 8,
Enqueue, the queue is: 2, 3, 4, 5, 6, 7, 8, 9,
Enqueue, the queue is: 2, 3, 4, 5, 6, 7, 8, 9, 10,
Queue full.
Enqueue, the queue is: 2, 3, 4, 5, 6, 7, 8, 9, 10,
Dequeue 9 elements , and the queue is: empty
Dequeue, the queue is: empty
Enqueue, the queue is: 10,
??有了上面的队列后,下面先说明一下深度优先搜索(Depth First Search)和广度优先搜索(Breadth First Search),然后通过广度优先搜索实现层序遍历1。
??人生苦短,以后文中没写的,都属于 不言自明(懒得写)的东西。
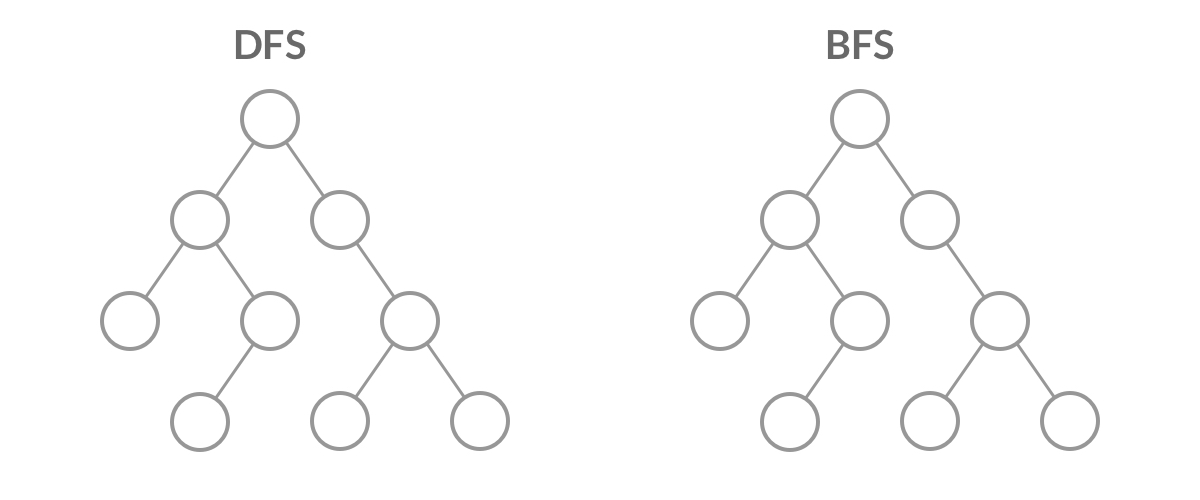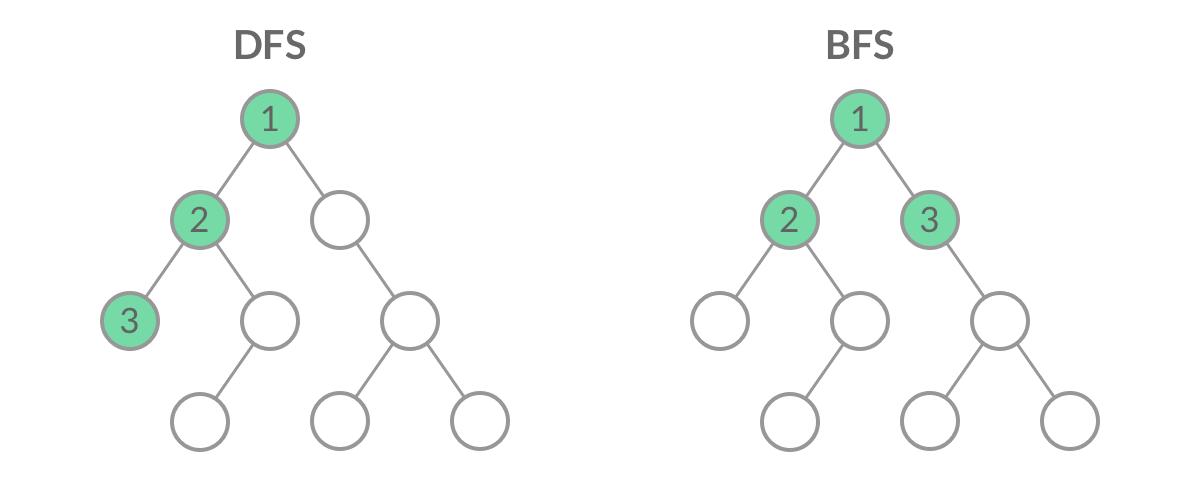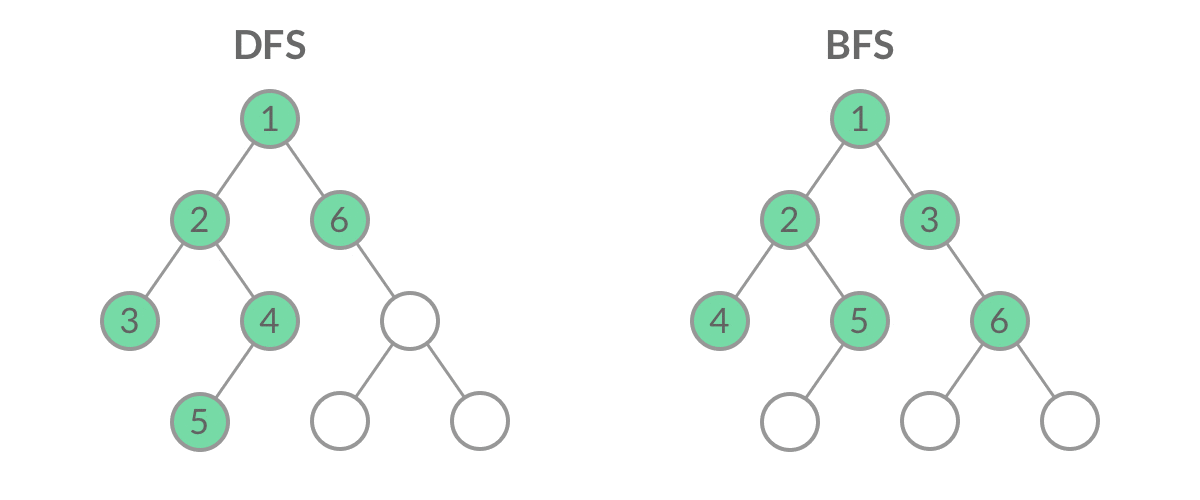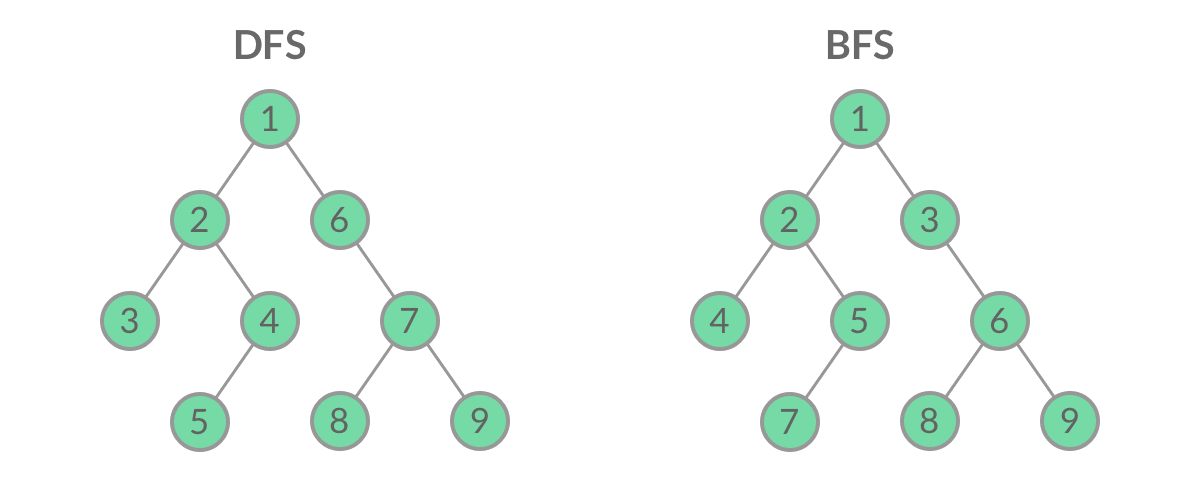
DFS:
void DepthFirstSearch(TreeNode root) [
if (root == null) { return; }
DepthFirstSearch(root.left);
DepthFirstSearch(root.right);
}// of DepthFirstSearch(TreeNode)
BFS:
void BreadthFirstSearch(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll(); // Java的pop写作poll()
if (node.left != null) {
queue.add(node.left );
} // of if
if (node.right != null){
queue. add(node.right);
} // of if
} // of while
}// of BreadthFirstSearch(TreeNode)
或
void BreadthFirstSearch(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
TreeNode node = queue.poll(); // Java的pop写作poll()
do {
if (node.left != null) {
queue.add(node.left );
} // of if
if (node.right != null){
queue.add(node.right);
} // of if
node = queue.poll();
} while (!queue.isEmpty());
}// of BreadthFirstSearch(TreeNode)
??ArrayDeque是Deque接口的一个实现类,使用了可变数组,所以没有容量上的限制。可以作为栈来使用,效率高于Stack;也可以作为队列来使用,效率高于LinkedList。
??需要注意的是,ArrayDeque不支持null值。同时,ArrayDeque是线程不安全的,在没有外部同步的情况下,不能再多线程环境下使用。
??学完数据结构后,多利用Java自己有的轮子!
??DepthFirstSearch调用了栈,我们前面已经用了很多了,只是没有单独提出来说,如前面的先序遍历:
public void preOrderVisit() {
// System.out.print("" + value + " ");
if (leftChild != null) {leftChild.preOrderVisit();}
if (rightChild != null) {rightChild.preOrderVisit();}
}// Of preOrderVisit
??注意,深度指纵向,广度指横向,这里的先序遍历是DFS,中序遍历和后序遍历实质上也都是DFS。
??下面用BFS实现层序遍历。
??「BFS 遍历」、「层序遍历」、「最短路径」实际上是递进的关系。在 BFS 遍历的基础上区分遍历的每一层,就得到了层序遍历。在层序遍历的基础上记录层数,就得到了最短路径(这个以后再学习)。

??先仔细分析BFS遍历和层序遍历的差异。注意下表队列中元素的变化。
| while循环中的第几次 | 出队元素 | 入队后的队中元素 |
|---|---|---|
| 0 | 无 | 1 |
| 1 | 1 | 无 + (1的左右子树)2 3 |
| 2 | 2 | 3 + (2的左右子树)4 5 |
| 3 | 3 | 4 5 + (3的左右子树)6 |
| 4 | 4 | 5 6 + (4的左右子树)无 |
| 5 | 5 | 6 + (5的左右子树)7 |
| 6 | 6 | 7 + (6的左右子树)8 9 |
| …… | 剩余依次出 | 无 |
??可以看到第2次while循环中队列变成了3 4 5,即即包含第1层的3又包含第2层的4 5。
??而每一次循环实际上是将当前出队的节点的左右子树的根入队,比如表中的“+ (1的左右子树)2 3”。
??那么,如果能先将这一层的元素出队,就自然将下一层的所有元素依次入队了,然后对下一层进行相同处理。
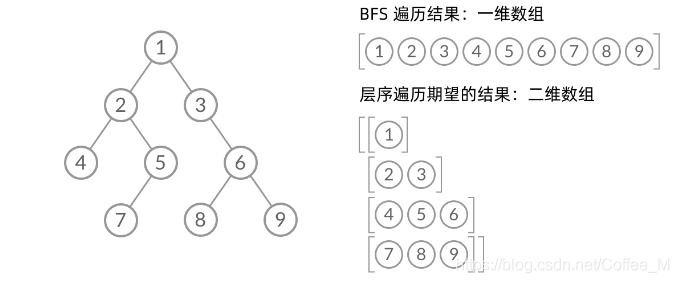
??乍一看来,这个层序遍历顺序和 BFS 是一样的,我们可以直接用 BFS 得出层序遍历结果。然而,层序遍历可以返回一个二维数组。而 BFS 的遍历结果只是一个一维数组,无法区分每一层。
??注意,是一口气处理完这一层的所有结点(一个循环),换言之,加一个局部变量,在每一层遍历开始前,先记录队列中的结点数量(注意,层序遍历中,每层开始前记录的是整层的节点数),然后根据元素个数先把一层处理完(每出队一个它对应的下层就入队了,这层出队完下层就全部入队了),然后再遍历下层。
??总体是一个嵌套循环,外层大循环本来为所有层,内层循环为该层的所有节点。外层循环在具体实现时,采用了一种简单的实现方式,所有层执行完则队列为空,那么队列非空就一直执行,这样的while(非空)循环取代了逻辑上的for(每层)循环。
??
??下面既是以Java中接口和实现类(Queue、TreeNode、ArrayDeque<TreeNode>)表示的代码,又是逻辑上的伪代码。
void levelOrderTraversal(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
int NumPerLayer = queue.size();
for (int i = 0; i < NumPerLayer; i++) {
TreeNode node = queue.poll();
if (node.left != null) {queue.add(node.left);}
if (node.right != null) {queue.add(node.right);}
} // of for i
} // of while
} // of levelOrderTraversal(TreeNode)
??或用do while循环;并将变量在循环外声明。修改如下:
void levelOrderTraversal(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
int NumPerLayer = queue.size();
TreeNode node;
do {
for (int i = 0; i < NumPerLayer; i++) {
node = queue.poll();
if (node.left != null) {queue.add(node.left);}
if (node.right != null) {queue.add(node.right);}
} // of for i
NumPerLayer = queue.size();
} while (!queue.isEmpty());
} // of levelOrderTraversal(TreeNode)
??在有了上面对广度优先遍历(BFS)和层序遍历(level order traversal)的分析后,下面实现对二叉树节点的位置和值的存储。
??首先是基于广度优先遍历的一种实现,该实现方式利用了完全二叉树(显然包括完美二叉)中,任意根节点与左、右子节点的数学关系:
n
l
e
f
t
C
h
i
l
d
=
2
n
r
o
o
t
,
n
r
i
g
h
t
C
h
i
l
d
=
2
n
r
o
o
t
+
1
n_{\rm{leftChild}}=2n_{\rm{root}}, n_{\rm{rightChild}}=2n_{\rm{root}}+1
nleftChild?=2nroot?,nrightChild?=2nroot?+1
??上面
n
r
o
o
t
n_{\rm{root}}
nroot?、
n
l
e
f
t
C
h
i
l
d
n_{\rm{leftChild}}
nleftChild?、
n
r
i
g
h
t
C
h
i
l
d
n_{\rm{rightChild}}
nrightChild?分别表示任意子树的根节点、根的左儿子、根的右儿子的序号(从1开始计数),如

给一个巧妙的证明:
??以上面的序号为五的根和它序号为十的左儿子为例。5加上后面的六、七这2个节点共7个节点,即
2
3
?
1
2^3-1
23?1,同样的十要加上六、七下面二叉的4个节点和十的1个兄弟,共
2
4
?
1
2^4-1
24?1。
??更一般的,记5为任意的
n
r
o
o
t
n_{\rm{root}}
nroot?,后面要加的共
m
m
m个,共
k
k
k层,则
n
r
o
o
t
+
m
=
2
k
?
1
n
l
e
f
t
C
h
i
l
d
+
2
m
+
1
=
2
k
+
1
?
1
\begin{aligned} n_{\rm{root}}+m &= 2^k-1\\ n_{\rm{leftChild}}+2m+1 &= 2^{k+1}-1 \end{aligned}
nroot?+mnleftChild?+2m+1?=2k?1=2k+1?1???化简即证。
??注意这里证的是节点个数的关系,即从1开始。如果是从0开始的下标,比如下面的代码,那么容易由上面的公式得到 n l e f t C h i l d + 1 = 2 ( n r o o t + 1 ) → n l e f t C h i l d = 2 n r o o t + 1 n_{\rm{leftChild}}+1=2(n_{\rm{root}}+1)\to n_{\rm{leftChild}}=2n_{\rm{root}}+1 nleftChild?+1=2(nroot?+1)→nleftChild?=2nroot?+1
??好了,在上面的基础上,我们先给出第一个由breadth first traversal给出的二叉树的存储:
/**
* The values of nodes according to breadth first traversal.
*/
char[] valuesArray;
/**
* The indices in the complete binary tree.
*/
int[] indicesArray;
/**
* Convert the tree to data arrays, including a char array and an int array. The
* results are stored in two member variables.
*
* @see #valuesArray
* @see #indicesArray
*/
public void toDataArrays() {
// Initialize arrays.
int tempLength = getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
int i = 0;
// Traverse and convert at the same time.
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this); // Before we start BFS while loop, the queue needs the root node,...
CircleIntQueue tempIntQueue = new CircleIntQueue();
tempIntQueue.enqueue(0); // and the index of root is 0.
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
int tempIndex = tempIntQueue.dequeue();
while (tempTree != null) {
valuesArray[i] = tempTree.value;
indicesArray[i] = tempIndex;
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(tempIndex * 2 + 1);
} // Of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
tempIntQueue.enqueue(tempIndex * 2 + 2);
} // Of if
tempTree = (BinaryCharTree) tempQueue.dequeue();
tempIndex = tempIntQueue.dequeue();
} // Of while
// do {...} while (tempTree != null);
}// Of toDataArrays
在前一节的class BinaryCharTree中加入上述代码后,再在main方法中加入如下测试语句:
tempTree.toDataArrays();
System.out.println("The values are: " + Arrays.toString(tempTree.valuesArray));
System.out.println("The indices are: " + Arrays.toString(tempTree.indicesArray));
??新的结果:
The values are: [a, b, c, d, e, f, g]
The indices are: [0, 1, 2, 4, 5, 9, 10]
??回顾整个过程,其实不是完全意义上的层序遍历,因为其实没有层的概念,尽管和层序遍历具有相同的输出。上面的储存实质就是,跟着BFS的一维遍历,同时根据额外的信息(左、右节点与父节点的数量关系,但如果不给出,则需要更多的循环判断),然后在子节点入关于节点的队时,新增一个序号入另一个专门存位置的队列。
??那么,下面仿前面代码,给出层序遍历的实现。为了便于理解,先给出最简功能的形式:
public void levelOrderTraversal() {
valuesArray = new char[this.getNumNodes()];
int i = 0;
// level order traversal
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this);
while (!tempQueue.isEmpty()) {
int NumPerLayer = tempQueue.size();
for (int k = 0; k < NumPerLayer; k++) {
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
valuesArray[i++] = tempTree.value;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
} // of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
} // of if
} // of for j
} // of while
} // of levelOrderTraversal()
??注意,这里的for循环中,我采用了在for 循环内定义变量(BinaryCharTree tempTree = …),这会多占用栈空间,每次循环都要重复定义局部变量,而如果放在循环体外,每次只要移动引用指向的堆内存地址即可,不必重新申请内存空间了,一直用的是同一块内存空间,效率比较高。但是栈内存的分配非常之快,而且循环外定义的话,变量的作用域就大了,也即放循环里面遵循变量最小作用域的理念。
??不过一般而言,还是要放外面更好,放里面主要是简洁,阅读性更好,增加的消耗在这里是极小的。后面我放外面了……
??再给出实现完整功能的形式,其实就是在上面代码的基础上根据需求添加功能,这也指出了在写代码时先实现最基础的,再不断完善相似功能,添加新功能:
public void levelOrderTraversal() {
levelOrderTraversal(this, 0);
}// of levelOrderTraversal()
private void levelOrderTraversal(BinaryCharTree root, int indexOfRoot) {
// Initialize arrays.
int tempLength = root.getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
// the index in the arrays to store.
int i = 0;
// the index of the layer.
int j = 1;
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(root);
CircleIntQueue tempIntQueue = new CircleIntQueue();
tempIntQueue.enqueue(indexOfRoot);
int NumPerLayer;
BinaryCharTree tempTree;
int tempIndex;
while (!tempQueue.isEmpty()) {
NumPerLayer = tempQueue.size();
for (int k = 0; k < NumPerLayer; k++) {
tempTree = (BinaryCharTree) tempQueue.dequeue();
valuesArray[i] = tempTree.value;
tempIndex = tempIntQueue.dequeue();
indicesArray[i] = tempIndex;
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(tempIndex * 2 + 1);
} // of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
tempIntQueue.enqueue(tempIndex * 2 + 2);
} // of if
} // of for j
System.out.println("The number of element in " + (j++) + "th level is: " + NumPerLayer);
} // of while
} // of levelOrderTraversal(BinaryCharTree, int)
??上面这些写成一个private和一个public的方式,好处是明确指出这个方法其实对任意节点处都是可以开始的,只需要指出节点和节点的起始序号即可,更能理解为什么将方法也称为函数。同时private操作更好的保护了数据。
??此外,层序遍历显然可以比BFS多做更多的事情,这里只是简单指出了每层有多少节点。
??新的结果:
The number of element in 1th level is: 1
The number of element in 2th level is: 2
The number of element in 3th level is: 2
The number of element in 4th level is: 2
The values are: [a, b, c, d, e, f, g]
The indices are: [0, 1, 2, 4, 5, 9, 10]
day23 使用具有通用性的队列
??昨天使用的队列有两种: 存储二叉树节点的队列,存储整数的队列。难道要为每种类型单独写一个队列? 这样显然没有充分利用代码的复用性. 实际上, 我们只需要一个存储对象的队列就够啦!
??Java 里面, 所有的类均为 Object 类的 (直接或间接) 子类. 如果不写就默认为直接子类. 例如public class CircleObjectQueue; 等价于 public class CircleObjectQueue extends Object;。
??存储对象的队列,实际上是存储对象的地址 (引用、指针)。 因此,可以存储任何类的对象 (的引用)。
??可以通过强制类型转换将对象转成其本身的类别,例如前面程序 tempTree = (BinaryCharTree) tempQueue.dequeue(); ,括号中的类型即表示强制类型转换。
??Java 本身将 int, double, char 分别封装到 Integer, Double, Char 类。
??下面跟随原作者见识一下它的威力吧。
public void toDataArrays() {
// Initialize arrays.
int tempLength = getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
// The index in the two arrays for storage.
int i = 0;
// BFS:
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this);
CircleObjectQueue tempIntQueue = new CircleObjectQueue();
tempIntQueue.enqueue(Integer.valueOf(0));
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
Integer tempIndex = (Integer) tempIntQueue.dequeue();
do {
valuesArray[i] = tempTree.value;
indicesArray[i] = tempIndex.intValue();
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(Integer.valueOf(tempIndex * 2 + 1));
} // Of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
tempIntQueue.enqueue(Integer.valueOf(tempIndex * 2 + 2));
} // Of if
tempTree = (BinaryCharTree) tempQueue.dequeue();
tempIndex = (Integer) tempIntQueue.dequeue();
} while (tempTree != null);
}// Of toDataArrays
??结果:
和之前一样哈 ! ! !
day24 二叉树的建立
??只增加了一个构造方法,相当于第 22 天的逆过程。
??个人添加了有限性验证。
??下标小心容易出错,下标从0开始真是一个非常糟糕的设计,为了一点点性能,让代码和算法分离,让计算机和数学多了一个坑,让人精力用在这些愚蠢的地方。
??补充:在完全二叉树的排序下,任意序号为n的节点(从0开始,便于代码对照,虽然但蛮蠢的)的父节点的序号为Java中的 ( n ? 1 ) / 2 (n-1)/2 (n?1)/2,java的除是向靠近0的方向取整,这里是整数即向下取整。数学关系很简单,不想说明了,下标的加1减1这些非常low的事情,让我根本提不起为这些蠢事说明的性质。下一门主流计算机语言务必解决下标从0开始这个糟糕的设计。
/**
*********************
* The second constructor.
*
* @param paraDataArray The array for data.
* @param paraIndicesArray The array for indices.
* @throws Exception
*********************
*/
public BinaryCharTree(char[] paraDataArray, int[] paraIndicesArray) {
// Step 1. Use a sequential list to store all nodes.
int tempNumNodes = paraIndicesArray.length;
BinaryCharTree[] tempAllNodes = new BinaryCharTree[tempNumNodes];
for (int i = 0; i < tempNumNodes; i++) {
tempAllNodes[i] = new BinaryCharTree(paraDataArray[i]);
} // Of for i
// Step 2: Link these nodes and check the validity.
int count = 0;
boolean okToLink = true;
if (paraDataArray.length != paraIndicesArray.length) {
okToLink = false;
System.out.println("The data cannot make a tree, as the 2 Arraies' lengthes are not equal.");
} // of if
for (int i = 0; i < tempNumNodes - 1; i++) {
if (paraIndicesArray[i] > paraIndicesArray[tempNumNodes - 1]) {
okToLink = false;
System.out.println("The data cannot make a tree, as the last node's index is not the max.");
} // of if
} // of for i
for (int i = 0; okToLink && i < tempNumNodes - 1; i++) {
for (int j = i + 1; okToLink && j < tempNumNodes; j++) {
if (paraIndicesArray[j] == paraIndicesArray[i] * 2 + 1) {
tempAllNodes[i].leftChild = tempAllNodes[j];
System.out.println("Node[" + i + "]:" + tempAllNodes[i].value + " 's leftChild is Node[" + j
+ "]: " + tempAllNodes[j].value);
count++;
// Validity check
if (count != j) {
System.out.println("The data cannot make a tree, as Node[" + i
+ "]'s rightChild cannot be Node[" + j + "]");
okToLink = false;
break;
} // of if
continue; // Not break this for-j loop, just skip this cycle.
} // of if
if (paraIndicesArray[j] == paraIndicesArray[i] * 2 + 2) {
tempAllNodes[i].rightChild = tempAllNodes[j];
System.out.println("Node[" + i + "]:" + tempAllNodes[i].value + " 's rightChild is Node[" + j
+ "]: " + tempAllNodes[j].value);
count++;
// Validity check
if (count != j) {
System.out.println("The data cannot make a tree, as Node[" + i
+ "]'s rightChild cannot be Node[" + j + "]");
okToLink = false;
break;
} // of if
break; // Now we can break this for-j loop, get to next i;
} // of if
} // of for j
} // of for i
// Validity check: the last node must be linked. if so, the validity check above
// could find possible error.
if (okToLink) {
boolean isLinked = false;
int temp = (paraIndicesArray[tempNumNodes - 1] - 1) / 2; // the index of the parent of the last node.
for (int i = 0; i <= temp; i++) {
if (paraIndicesArray[i] == temp) {
isLinked = true;
break;
} // of if
} // of for i
if (!isLinked) {
System.out.println("The data cannot make a tree, as lastNode does not have a parent");
} // of if
}
// Step 3. Link the root to the first node.
value = tempAllNodes[0].value;
leftChild = tempAllNodes[0].leftChild;
rightChild = tempAllNodes[0].rightChild;
}// Of the the second constructor
??main添加测试:
char[] tempCharArray = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H' };
int[] tempIndicesArray = { 0, 1, 2, 4, 5, 7, 12, 14 };
BinaryCharTree tempTree2 = new BinaryCharTree(tempCharArray, tempIndicesArray);
System.out.println("\r\nPreorder visit:");
tempTree2.preOrderVisit();
System.out.println("\r\nIn-order visit:");
tempTree2.inOrderVisit();
System.out.println("\r\nPost-order visit:");
tempTree2.postOrderVisit();
??新的测试结果:
Node[0]:A 's leftChild is Node[1]: B
Node[0]:A 's rightChild is Node[2]: C
Node[1]:B 's rightChild is Node[3]: D
Node[2]:C 's leftChild is Node[4]: E
Node[4]:E 's rightChild is Node[6]: G
The data cannot make a tree, as Node[4]'s rightChild cannot be Node[6]
Preorder visit:
A B D C E G
In-order visit:
B D A E G C
Post-order visit:
D B G E C A
day25、26 二叉树深度遍历的栈实现
??首先给出Object的栈:
package dataStructure.stack;
/**
* Circle Object queue.
*
* @author Fan Min minfanphd@163.com.
* @learner CatInCoffee.
*/
public class ObjectStack {
public static final int MAX_DEPTH = 10;
/**
* The actual depth.
*/
int depth;
/**
* The data Array
*/
Object[] data;
// Construct an empty sequential list.
public ObjectStack() {
depth = 0;
data = new Object[MAX_DEPTH];
}// Of the first constructor
public String toString() {
String resultString = "";
for (int i = 0; i < depth; i++) {
resultString += data[i];
} // Of for i
return resultString;
}// Of toString
/**
* Push an element.
*
* @param paraObject The given object.
* @return Success or not.
*/
public boolean push(Object paraObject) {
if (depth == MAX_DEPTH) {
System.out.println("Stack full.");
return false;
} // Of if
data[depth++] = paraObject;
return true;
}// Of push
/**
* Pop an element.
*
* @return The object at the top of the stack.
*/
public Object pop() {
if (depth == 0) {
System.out.println("Nothing to pop.");
return '\0';
} // of if
Object resultObject = data[depth - 1];
depth--;
return resultObject;
}// Of pop
public boolean isEmpty() {
if (depth == 0) {
return true;
} // Of if
return false;
}// Of isEmpty
public static void main(String args[]) {
ObjectStack tempStack = new ObjectStack();
for (char ch = 'a'; ch < 'l'; ch++) {
tempStack.push(Character.valueOf(ch));
System.out.println("The current stack is: " + tempStack);
} // Of for i
Character tempChar;
for (int i = 0; i < 11; i++) {
tempChar = (Character) tempStack.pop();
System.out.print("Poped: " + tempChar.charValue());
System.out.println(" The current stack is: " + tempStack);
} // Of for i
}// Of main
}// of class ObjectStack
??结果:
The current stack is: a
The current stack is: ab
The current stack is: abc
The current stack is: abcd
The current stack is: abcde
The current stack is: abcdef
The current stack is: abcdefg
The current stack is: abcdefgh
The current stack is: abcdefghi
The current stack is: abcdefghij
Stack full.
The current stack is: abcdefghij
Poped: j The current stack is: abcdefghi
Poped: i The current stack is: abcdefgh
Poped: h The current stack is: abcdefg
Poped: g The current stack is: abcdef
Poped: f The current stack is: abcde
Poped: e The current stack is: abcd
Poped: d The current stack is: abc
Poped: c The current stack is: ab
Poped: b The current stack is: a
Poped: a The current stack is:
Nothing to pop.
Poped:
??然后是个人理解和实现的:?? 基于栈实现的深度遍历
??
day27 Hanoi 塔问题
??这里的hanoi塔我是自己设计的,我个人觉得挺巧妙的。
??首先,我理解的Hanoi塔其实就是3个节点Node。每个Node保存数据用了一个栈,一般的Hanoi分析3个栈已经足够了(以至于根本用不上单独设计一个Node),但是这背后其实有更深的关联。
??隐藏关系,这3个Node其实是存在位置关系的,一般来说是把Hanoi的位置放进参数里,但我觉得还可以更巧妙些,不妨规定第一个Node是起始的第一个塔,第二个Node是最终转移到的塔,第三个Node是作为中间媒介的塔,那么函数的参数就似乎可以省略位置信息。
??是的,似乎确实可以,但一方面要挖掘更深入的Hanoi关系,另一方面需要在Node节点中加入隐含的位置关系,那就是到另2个Node的链。我借鉴双链表的经验,让Node有prev和next2个链到令2个节点。此外,Hanoi的操作,抽象成:函数hanoi(n),即只有1个参数n,表示最初的Hanoi塔层数。然后位置信息被隐藏为,从第一个栈全部转移到第二个栈。
??这时候,又有了新的问题,不给位置信息怎么递归的调用自己,因为我们知道Hanoi塔本身的解法是要递归的调用改变位置参数的自身函数的。
??宏观的说,我认为就是把参数的隐含关系总结出来,写成内部函数。结合Hanoi问题,首先n层Hanoi塔从a转移到b,实际上是,将a的前n-1层转移到c,然后把a最下面移到b,然后把c的n-1层移到b。这个过程就可以写递归方法了。仔细分析,上面的a移到c是当前Node移到prev节点,a移到b是当前Node移到next节点,对其他节点也是这两个方法,而且这两个移动的程序是相似的,因此可以写作Node类中的两个私有函数(注:这2个函数可以通过增加一个Node参数写作一个,但我不想,那样降低了代码阅读性)。原理大概这样,看代码吧,后面也给出了一般的解法,不过一般解法更适合打印每次出栈的结果……
??解法1:
package myProgrames;
import myList.myStack.MyLinkedStack;
/**
* Hanoi tower.
*
* @author CatInCoffee, 2021/7/26.
*/
public class Hanoi {
private static final int MaxNumOfLayers = 32;
private static class Node {
public Node next;
public Node prev;
public MyLinkedStack<Integer> dataStack = new MyLinkedStack<>();
public Node() {
this(-1, null, null);
}// of Node's first constructor
// If paraNum = -1, there is no data in the stack.
public Node(int paraNum, Node paraNext, Node paraPrev) {
for (int i = 0; i < paraNum; i++) {
dataStack.push(Integer.valueOf(paraNum - i));
} // of for i
next = paraNext;
prev = paraPrev;
}// of Node's second constructor
/**
* forward Hanoi.
*
* The data in the stack of the current node transfers to the stack of the next.
*/
public void forwardHanoi(int n) {
if (n == 1) {
Integer temp = dataStack.pop();
next.dataStack.push(temp);
} else {
backwardHanoi(n - 1);
forwardHanoi(1);
prev.backwardHanoi(n - 1);
} // of if-else
}// of forwardHanoi(int)
/**
* backward Hanoi.
*
* The data in the current stack transfers to the stack of the previous node.
*/
public void backwardHanoi(int n) {
if (n == 1) {
Integer temp = dataStack.pop();
prev.dataStack.push(temp);
} else {
forwardHanoi(n - 1);
backwardHanoi(1);
next.forwardHanoi(n - 1);
} // of if-else
}// of forwardHanoi(int)
}// of class Node
// *****************************************************************************************
Node start;
Node destination;
Node intermediary;
private int maxLayers;
private boolean okToHanoi = true;
// The default number of layers is 10.
public Hanoi() {
this(20);
}// of Hanoi's first constructor
public Hanoi(int n) {
if (n < 1 || n > MaxNumOfLayers) {
okToHanoi = false;
return;
} // of if
maxLayers = n;
destination = new Node();
intermediary = new Node();
start = new Node(n, destination, intermediary);
destination.next = intermediary;
destination.prev = start;
intermediary.next = start;
intermediary.prev = destination;
}// of Hanoi's second constructor
// *****************************************************************************************
public void hanoi() {
if (okToHanoi) {
hanoi(maxLayers);
} else {
System.out.print("Wrong parameter!");
} // of if else
}// of hanoi()
private void hanoi(int n) {
start.forwardHanoi(n);
}// of hanoi(int)
// *****************************************************************************************
public String toString() {
String s = (okToHanoi)
? ("{ " + start.dataStack.toString() + " ; " + destination.dataStack.toString() + " ; "
+ intermediary.dataStack.toString() + " }")
: "The number of layers is less than 0 or too big!!!";
return s;
}// of toString()
public static void main(String[] args) {
long startTime = System.currentTimeMillis();
long beginTime = System.nanoTime();
{
Hanoi test = new Hanoi(22);
System.out.println("The initial Hanoi tower: \n" + test);
test.hanoi();
System.out.println("After hanoi operation, the initial Hanoi tower: \n" + test);
}
long finishTime = System.currentTimeMillis();
long endTime = System.nanoTime();
System.out.println("The program running time: " + (finishTime - startTime) + " ms");
System.out.println("The program running time: " + (endTime - beginTime) + " ns");
}// of main
}// of class Hanoi
??结果:
The initial Hanoi tower:
{ { 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 } ; Empty ; Empty }
After hanoi operation, the initial Hanoi tower:
{ Empty ; { 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 } ; Empty }
The program running time: 84 ms
The program running time: 83881400 ns
??解法2:
package myProgrames;
import myList.myStack.MyLinkedStack;
/**
* The Second way to show Hanoi tower. This method is easier but not that
* skillful.
*
* @author CatInCoffee, 2021/7/27.
*/
public class Hanoii {
private static final int MaxNumOfLayers = 6;
private static class Node {
public MyLinkedStack<Integer> dataStack = new MyLinkedStack<>();
public Node() {
this(-1);
}// of Node's first constructor
// If numOfLayers = -1, there is no data in the stack.
public Node(int numOfLayers) {
for (int i = 0; i < numOfLayers; i++) {
dataStack.push(Integer.valueOf(numOfLayers - i));
} // of for i
}// of Node's second constructor
}// of class Node
// *****************************************************************************************
Node start;
Node destination;
Node intermediary;
private boolean okToHanoi = true;
// The default number of layers is 10.
public Hanoii() {
this(5);
}// of Hanoi's first constructor
public Hanoii(int n) {
if (n < 1 || n > MaxNumOfLayers) {
okToHanoi = false;
return;
} // of if
destination = new Node();
intermediary = new Node();
start = new Node(n);
}// of Hanoi's second constructor
// *****************************************************************************************
private void hanoi(int n, Node paraStart, Node paraDestination, Node paraIntermediary) {
if (n == 1) {
Integer temp = paraStart.dataStack.pop();
paraDestination.dataStack.push(temp);
System.out.println(this);
} else if (okToHanoi) {
hanoi(n - 1, paraStart, paraIntermediary, paraDestination);
hanoi(1, paraStart, paraDestination, paraIntermediary);
hanoi(n - 1, paraIntermediary, paraDestination, paraStart);
} else {
System.out.println("Wrong parameter!");
} // of if
}// of hanoi(int)
// *****************************************************************************************
public String toString() {
String s = (okToHanoi)
? ("{ " + start.dataStack.toString() + " ; " + destination.dataStack.toString() + " ; "
+ intermediary.dataStack.toString() + " }")
: "Wrong parameter!!!";
return s;
}// of toString()
public static void main(String[] args) {
long startTime = System.currentTimeMillis();
{
Hanoii test = new Hanoii(5);
System.out.println("The initial Hanoi tower is: \n\t" + test + ",\nthe changing process of the stack is:\n");
test.hanoi(5, test.start, test.destination, test.intermediary);
// System.out.println("\nAfter hanoi operation, the Hanoi tower is: \n" + test);
}
long finishTime = System.currentTimeMillis();
System.out.print("\nThe program running time: " + (finishTime - startTime) + " ms");
}// of main
}// of class Hanoii
??结果:
The initial Hanoi tower is:
{ { 1 2 3 4 5 } ; Empty ; Empty },
the changing process of the stack is:
{ { 2 3 4 5 } ; { 1 } ; Empty }
{ { 3 4 5 } ; { 1 } ; { 2 } }
{ { 3 4 5 } ; Empty ; { 1 2 } }
{ { 4 5 } ; { 3 } ; { 1 2 } }
{ { 1 4 5 } ; { 3 } ; { 2 } }
{ { 1 4 5 } ; { 2 3 } ; Empty }
{ { 4 5 } ; { 1 2 3 } ; Empty }
{ { 5 } ; { 1 2 3 } ; { 4 } }
{ { 5 } ; { 2 3 } ; { 1 4 } }
{ { 2 5 } ; { 3 } ; { 1 4 } }
{ { 1 2 5 } ; { 3 } ; { 4 } }
{ { 1 2 5 } ; Empty ; { 3 4 } }
{ { 2 5 } ; { 1 } ; { 3 4 } }
{ { 5 } ; { 1 } ; { 2 3 4 } }
{ { 5 } ; Empty ; { 1 2 3 4 } }
{ Empty ; { 5 } ; { 1 2 3 4 } }
{ { 1 } ; { 5 } ; { 2 3 4 } }
{ { 1 } ; { 2 5 } ; { 3 4 } }
{ Empty ; { 1 2 5 } ; { 3 4 } }
{ { 3 } ; { 1 2 5 } ; { 4 } }
{ { 3 } ; { 2 5 } ; { 1 4 } }
{ { 2 3 } ; { 5 } ; { 1 4 } }
{ { 1 2 3 } ; { 5 } ; { 4 } }
{ { 1 2 3 } ; { 4 5 } ; Empty }
{ { 2 3 } ; { 1 4 5 } ; Empty }
{ { 3 } ; { 1 4 5 } ; { 2 } }
{ { 3 } ; { 4 5 } ; { 1 2 } }
{ Empty ; { 3 4 5 } ; { 1 2 } }
{ { 1 } ; { 3 4 5 } ; { 2 } }
{ { 1 } ; { 2 3 4 5 } ; Empty }
{ Empty ; { 1 2 3 4 5 } ; Empty }
The program running time: 2 ms
day28-30 Huffman 编码
??这里没有学习,我打算等后面学算法时再看。后面一段时间会先学习:散列、优先队列(堆)、排序、不相交集类、图论。
https://www.cnblogs.com/sbb-first-blog/p/13259728.html。 ??