【CVPR 2021】剪枝篇(二):Convolutional Neural Network Pruning with Structural Redundancy Reduction
论文地址:
https://arxiv.org/abs/2104.03438
主要问题:
现有的模型剪枝工作通常集中于删除网络中最不重要的卷积核,以实现紧凑的网络结构
在这项研究中作者声称结构冗余比寻找不重要的卷积核起更重要的作用
主要思路:
作者首先从冗余减少的角度对模型剪枝问题进行统计建模,发现结构冗余最多的层中的剪枝优于在所有层中修剪最不重要的卷积核
通过这一发现,我们提出了一种基于结构冗余减小(SSR)的层自适应通道剪枝方法,通过为CNN的每个卷积层建立一个图,并使用与图相关的两个量(即 ? ? ?- ??覆盖数和商空间大小)作为每一层冗余的测量
理论分析:
基本定义:
假设我们有两个CNN,它们分别带有 m m m 和 n n n 个卷积,其中 n > > m n>>m n>>m
假设 { ξ 1 , ξ 2 , . . . , ξ m } \{\xi_1,\xi_2,...,\xi_m\} {ξ1?,ξ2?,...,ξm?} 和 { η 1 , η 2 , . . . , η n } \{\eta_1,\eta_2,...,\eta_n\} {η1?,η2?,...,ηn?} 是一维正随机变量(RV),表示每个卷积对网络性能的贡献
例如,卷积的贡献可以表示为修剪该卷积后训练精度下降或训练损失变化的绝对值
为了方便起见,我们称这两层为 ξ ξ ξ层和 η η η层
公式和声明:
如果一个层具有更高的冗余,那么我们将裁剪该层中的卷积,无论是随机地还是选择性地,都优于修剪所有层中最不重要的卷积
我们选取正的常量 a , b > 0 a,b>0 a,b>0,并使用随机事件 ( ∑ i = 1 m ξ i ≥ a ) (\sum_{i=1}^m\xi_i\geq a) (∑i=1m?ξi?≥a) 和 ( ∑ i = 1 n η i ≥ b ) (\sum_{i=1}^n\eta_i\geq b) (∑i=1n?ηi?≥b) 来表示 ξ ξ ξ 层和 η η η 层是否“表现的好”
因此系统的性能(即整个神经网络) p p p 就可以通过上述两个事件的概率的总和来衡量
并且 p o p_o po? 越大表示由 ( p o ) (p_o) (po?) 表示的系统性能越好
一个自然的问题是,如果我们从网络中裁剪某一个卷积,即从 { ξ 1 , ξ 2 , . . . , ξ m , η 1 , η 2 , . . . , η n } \{ξ_1,ξ_2,...,ξ_m,η_1,η_2,...,η_n\} {ξ1?,ξ2?,...,ξm?,η1?,η2?,...,ηn?}中删除一个变量,系统性能如何变化?
作者将上述裁剪行为分成以下五种情况:
- 没有剪枝;
- 在 η η η 层中随机裁剪一个卷积,而没有失去一般性(我们假设最后一个 η n η_n ηn? 被裁剪);
- 裁剪 η η η 层中最不重要的过滤器 η  ̄ = m i n { η 1 , . . . , η n } \underlineη=min\{η_1,...,η_n\} η?=min{η1?,...,ηn?};
- 裁剪 ξ ξ ξ 层中最不重要的过滤器 ξ  ̄ = m i n { ξ 1 , . . . , ξ n } \underlineξ=min\{ξ_1,...,ξ_n\} ξ?=min{ξ1?,...,ξn?};
- 裁剪全局最不重要的卷积,即 m i n { ξ  ̄ , η  ̄ } min\{\underlineξ,\underlineη\} min{ξ?,η?};
上述五种情况的系统性能公式分别如下:
1. ?? p o = P ( ∑ i = 1 m ξ i ≥ a ) + P ( ∑ i = 1 n η i ≥ b ) 1.\space\space p_o=P(\sum_{i=1}^m\xi_i\geq a)+P(\sum_{i=1}^n\eta_i\geq b) 1.??po?=P(∑i=1m?ξi?≥a)+P(∑i=1n?ηi?≥b)
2. ?? p η r = P ( ∑ i = 1 m ξ i ≥ a ) + P ( ∑ i = 1 n ? 1 η i ≥ b ) 2.\space\space p_{ηr}=P(\sum_{i=1}^m\xi_i\geq a)+P(\sum_{i=1}^{n-1}\eta_i\geq b) 2.??pηr?=P(∑i=1m?ξi?≥a)+P(∑i=1n?1?ηi?≥b)
3. ?? p η  ̄ = P ( ∑ i = 1 m ξ i ≥ a ) + P ( ∑ i = 1 n η i ? η  ̄ ≥ b ) 3.\space\space p_{\underlineη}=P(\sum_{i=1}^m\xi_i\geq a)+P(\sum_{i=1}^n\eta_i-\underlineη\geq b) 3.??pη??=P(∑i=1m?ξi?≥a)+P(∑i=1n?ηi??η?≥b)
4. ?? p ξ  ̄ = P ( ∑ i = 1 m ξ i ? ξ  ̄ ≥ a ) + P ( ∑ i = 1 n η i ≥ b ) 4.\space\space p_{\underlineξ}=P(\sum_{i=1}^m\xi_i-\underlineξ\geq a)+P(\sum_{i=1}^n\eta_i\geq b) 4.??pξ??=P(∑i=1m?ξi??ξ?≥a)+P(∑i=1n?ηi?≥b)
5. ?? p g = m m + n p ξ  ̄ + n m + n p η  ̄ 5.\space\space p_g=\frac{m}{m+n}p_{\underlineξ}+\frac{n}{m+n}p_{\underline\eta} 5.??pg?=m+nm?pξ??+m+nn?pη??
其中 a a a 和 b b b 可以被认为是一个阈值,只要一层中卷积的总贡献大于阈值,我们就认为它就没有性能损失
而如果一个层冗余过多(在模型的上下文中有太多卷积),那么修剪一些卷积后的总贡献很可能仍然大于阈值
值得注意的是 0 ≤ η n ? η  ̄ ≤ η n 0\le\eta_n-\underline\eta\le\eta_n 0≤ηn??η?≤ηn?,即:
P ( ∑ i = 1 n ? 1 η i ≥ b ) ≤ P ( ∑ i = 1 n η i ? η  ̄ ≥ b ) ≤ P ( ∑ i = 1 n η i ≥ b ) P(\sum_{i=1}^{n-1}\eta_i\geq b)\le P(\sum_{i=1}^{n}\eta_i-\underline\eta\geq b)\le P(\sum_{i=1}^{n}\eta_i\geq b) P(∑i=1n?1?ηi?≥b)≤P(∑i=1n?ηi??η?≥b)≤P(∑i=1n?ηi?≥b)
也就是说 p η r ≤ p η  ̄ ≤ p o p_{\eta r}\le p_{\underline\eta}\le p_o pηr?≤pη??≤po?
对于 η η η 层中的卷积,我们自然地假设卷积对网络性能的贡献不可能是无限的,即卷积贡献的方差是一致有界的:
? C 1 > 0 , s . t . ? D η i ≤ C 1 , i = 1 , 2 , . . . , n \exist C_1>0,s.t. \space\mathbb{D}_{\eta_i}\le C_1,i=1,2,...,n ?C1?>0,s.t.?Dηi??≤C1?,i=1,2,...,n
由切比雪夫不等式,对于任意 ? > 0 \epsilon>0 ?>0,有:
P ( 1 n ∣ ∑ i = 1 n ( η i ? E η i ) ∣ ≥ ? ) ≤ D ( ∑ i = 1 n η i ) ? 2 n 2 P(\frac{1}{n}|\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i)|\ge\epsilon)\le\frac{\mathbb{D}(\sum^n_{i=1}\eta_i)}{\epsilon^2n^2} P(n1?∣∑i=1n?(ηi??Eηi?)∣≥?)≤?2n2D(∑i=1n?ηi?)?
我们可以得到:
C o v ( η i , η j ) ≤ D η i ? D η j ≤ C 1 Cov(\eta_i,\eta_j)\le\sqrt{\mathbb{D}_{\eta_i}\cdot\mathbb{D}_{\eta_j}}\le C_1 Cov(ηi?,ηj?)≤Dηi???Dηj???≤C1?
我们进一步定义,在 η \eta η 层中共有 C 2 n ( 0 ≤ C 2 ≤ 1 ) C_2n(0\le C_2\le1) C2?n(0≤C2?≤1) 对相关卷积,也就是说:
# { ( i , j ) : C o v ( η i , η j ) ≠ 0 , i ≠ j , ? i , j = 1 , . . . , n } ≤ C 2 n \#\{(i,j):Cov(\eta_i,\eta_j)\ne0,i\ne j,\space i,j=1,...,n\}\le C_2n #{(i,j):Cov(ηi?,ηj?)?=0,i?=j,?i,j=1,...,n}≤C2?n
这样我们就可以得到:
D ( ∑ i = 1 n η i ) = ∑ i = 1 n D η i + ∑ i ≠ j C o v ( η i , η j ) ≤ C 1 n + C 1 C 2 n = C 1 ( 1 + C 2 ) n \begin{aligned} \mathbb{D}(\sum^n_{i=1}\eta_i)&=\sum^n_{i=1}\mathbb{D}\eta_i+\sum_{i\ne j}Cov(\eta_i,\eta_j) \\ &\le C_1n+C_1C_2n=C1(1+C_2)n \end{aligned} D(i=1∑n?ηi?)?=i=1∑n?Dηi?+i?=j∑?Cov(ηi?,ηj?)≤C1?n+C1?C2?n=C1(1+C2?)n?
再结合上式,有:
P ( 1 n ∣ ∑ i = 1 n ( η i ? E η i ) ∣ ≥ ? ) ≤ C 1 ( 1 + C 2 ) ? 2 n 2 → 0 P(\frac{1}{n}|\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i)|\ge\epsilon)\le\frac{C_1(1+C_2)}{\epsilon^2n^2}\rightarrow0 P(n1?∣∑i=1n?(ηi??Eηi?)∣≥?)≤?2n2C1?(1+C2?)?→0
这表示假定 η \eta η 层中卷积数量 n n n 足够大(例如 n > 2 b ? o n>\frac{2b}{\epsilon_o} n>?o?2b?), 1 n ∑ i = 1 n ( η i ? E η i ) \frac{1}{n}\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i) n1?∑i=1n?(ηi??Eηi?) 概率上收敛到 0 0 0,也就是说:
1 n ∑ i = 1 n ( η i ? E η i ) → P 0 \frac{1}{n}\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i)\stackrel{P}{\rightarrow}0 n1?∑i=1n?(ηi??Eηi?)→P0
我们考虑卷积的贡献应该是整数,但是它可以非常小
也就是说对卷积贡献的期望具有统一的正下界:
? ? 0 > 0 , s . t . ? E η i ≤ ? 0 , i = 1 , 2 , . . . , n \exist \epsilon_0>0,s.t. \space\mathbb{E}_{\eta_i}\le \epsilon_0,i=1,2,...,n ??0?>0,s.t.?Eηi??≤?0?,i=1,2,...,n
根据之前的推导,我们可以得出:
P ( 1 n ∑ i = 1 n ( η i ? E η i ) > ? ? 0 2 ) = P ( ∑ i = 1 n η i > ∑ i = 1 n E η i ? ? 0 2 n ) = P ( ∑ i = 1 n η i > ? 0 2 n + ∑ i = 1 n ( E η i ? ? 0 ) ) ≤ P ( ∑ i = 1 n η i > ? 0 2 n ) ≤ P ( ∑ i = 1 n η i > b ) \begin{aligned} P(\frac{1}{n}\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i)>-\frac{\epsilon_0}{2})&=P(\sum^n_{i=1}\eta_i>\sum^n_{i=1}\mathbb{E}\eta_i-\frac{\epsilon_0}{2}n) \\ &=P(\sum^n_{i=1}\eta_i>\frac{\epsilon_0}{2}n+\sum^n_{i=1}(\mathbb{E}\eta_i-\epsilon_0)) \\ &\le P(\sum^n_{i=1}\eta_i>\frac{\epsilon_0}{2}n)\le P(\sum^n_{i=1}\eta_i>b) \end{aligned} P(n1?i=1∑n?(ηi??Eηi?)>?2?0??)?=P(i=1∑n?ηi?>i=1∑n?Eηi??2?0??n)=P(i=1∑n?ηi?>2?0??n+i=1∑n?(Eηi???0?))≤P(i=1∑n?ηi?>2?0??n)≤P(i=1∑n?ηi?>b)?
如果有 n → + ∞ n\rightarrow +\infty n→+∞,取极限并且考虑 1 n ∑ i = 1 n ( η i ? E η i ) → P 0 \frac{1}{n}\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i)\stackrel{P}{\rightarrow}0 n1?∑i=1n?(ηi??Eηi?)→P0,那么我们可以得到:
l i m n → ∞ P ( ∑ i = 1 n η i > b ) ≥ l i m n → ∞ P ( 1 n ∑ i = 1 n ( η i ? E η i ) > ? ? 0 2 ) = 1 lim_{n\rightarrow\infty}P(\sum^n_{i=1}\eta_i>b)\geq lim_{n\rightarrow\infty}P(\frac{1}{n}\sum^n_{i=1}(\eta_i-\mathbb{E}\eta_i)>-\frac{\epsilon_0}{2})=1 limn→∞?P(∑i=1n?ηi?>b)≥limn→∞?P(n1?∑i=1n?(ηi??Eηi?)>?2?0??)=1
l i m n → ∞ P ( ∑ i = 1 n η i ? η r > b ) ≥ l i m n → ∞ P ( 1 n ∑ i = 1 n η i ? η  ̄ > b ) = 1 lim_{n\rightarrow\infty}P(\sum^n_{i=1}\eta_i-\eta_r>b)\geq lim_{n\rightarrow\infty}P(\frac{1}{n}\sum^n_{i=1}\eta_i-\underline{\eta}>b)=1 limn→∞?P(∑i=1n?ηi??ηr?>b)≥limn→∞?P(n1?∑i=1n?ηi??η?>b)=1
然后如果 n n n 足够大,我们又有 p η r ≈ p η  ̄ ≈ p o p_{\eta r}\approx p_{\underline{\eta}}\approx p_o pηr?≈pη??≈po?
注意 p ξ  ̄ ≤ p o ≈ p η  ̄ p_{\underline{\xi}}\leq p_o\approx p_{\underline{\eta}} pξ??≤po?≈pη?? 并且 p g p_g pg? 是 p ξ  ̄ p_{\underline{\xi}} pξ?? 和 p η  ̄ p_{\underline{\eta}} pη?? 的加权均值
因此我们可以得到: p ξ  ̄ ≤ p g ≤ p η  ̄ p_{\underline{\xi}}\leq p_g\leq p_{\underline{\eta}} pξ??≤pg?≤pη??
这表明(即使是随机的)修剪层中冗余更大的卷积的性能优于在所有层中修剪最不重要的卷积
这个结论依赖于 n → + ∞ n→+∞ n→+∞的假设,而且这个假设可以在现实应用中放松,这样 p η ≥ p g p_η≥p_g pη?≥pg? 仍然近似有效(尽管不是在每个剪枝过程的选择步骤中)
具体实现:
基本符号:
模型剪枝:
假设一个CNN有 L L L 个层
对于第 i i i 层,输入和输出通道数分别表示为 N i N_i Ni? 和 N i + 1 N_{i+1} Ni+1?
因此 CNN 的参数 w w w 就可以写作: { W ( i ) ∈ R N i + 1 × N i × h i × w i , i = 1 , 2 , . . . , L } \{W^{(i)}\in\mathbb{R}^{N_{i+1}×N_i×h_i×w_i},i=1,2,...,L\} {W(i)∈RNi+1?×Ni?×hi?×wi?,i=1,2,...,L},其中 h i h_i hi? 和 w i w_i wi? 分别是卷积核的高和宽
通道剪枝的目标是找到一组在某些目标函数上优化的参数,例如 ∣ ∣ W ‘ ∣ ∣ 0 < K ||W`||_0<K ∣∣W‘∣∣0?<K,其中 ∣ ∣ ? ∣ ∣ 0 ||\cdot||_0 ∣∣?∣∣0? 表示 l 0 l_0 l0? 正则, K K K 用来限制 W ‘ W` W‘ 中非零卷积核数目
根据不同的配置,目标函数可以是最小化CNN的成本函数、训练精度的下降或重构误差等
图理论:
假设 X X X 是一个有限集,一个无向图可以表示为 ( X , E ) (X,E) (X,E),其中 E E E 是 X × X X×X X×X(或者写作 { ( x , x ) : x ∈ X } \{(x,x):x\in X\} {(x,x):x∈X}) 的一个对称子集
我们吧 x ∈ X x\in X x∈X 称作一个节点, ( x , y ) ∈ E (x,y)\in E (x,y)∈E 称作边
对于 x , y ∈ X x,y\in X x,y∈X,从 x x x 到 y y y 的路径是一个有限列表 { x 0 , x 1 , . . . , x n } ? X \{x_0,x_1,...,x_n\}\subset X {x0?,x1?,...,xn?}?X
而且如果上述路径存在,该路径也许不是唯一的
假设 d ( x , y ) d(x,y) d(x,y) 是从 x x x 到 y y y 的最短路径,并且当 x , y x,y x,y 不可达时记作 d ( x , y ) = + ∞ d(x,y)=+\infty d(x,y)=+∞
那么 d ( x , y ) d(x,y) d(x,y) 就可以看做一个整数值度量
补充:节点的 x x x 度是与节点 x x x 直接相连的边数
整体架构:
这个方法侧重于测量每个层中存在多少冗余,并从最冗余的层中修剪滤波器:
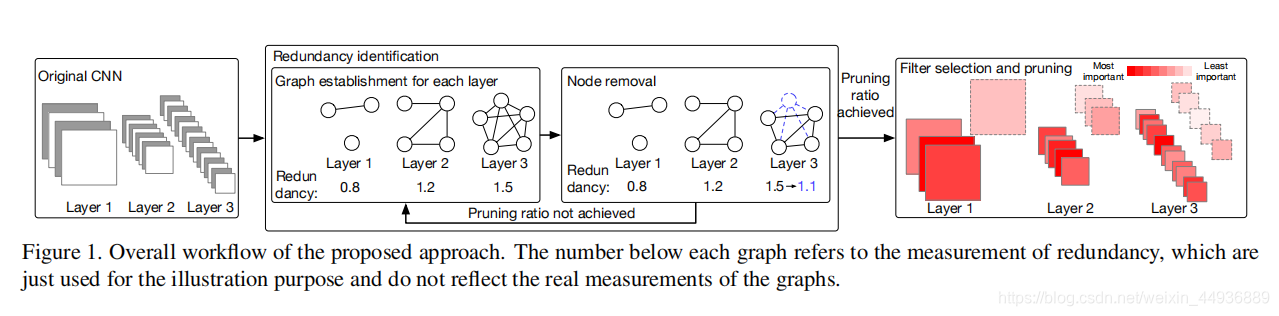
为了测量网络中的结构冗余,我们首先为每一层构建一个无向图,其中每个顶点表示一个卷积,并用卷积权重之间的距离定义边
我们使用与图相关的两个量(即商空间大小和 ? ? ? 覆盖数),作为每个图中存在多少冗余的度量,即每一层中存在的冗余
在每个步长的图建立和冗余量化之后,我们从具有最冗余的图中随机删除一个顶点及其相关边
然后我们重新计算下一次迭代的图重建后的冗余度
上述过程一直持续到达到优化目标(例如裁剪掉一定数量的卷积)
最后,我们根据具有一定卷积选择准则的每个图中剩余的顶点数对每一层的卷积进行裁剪
注意在裁剪阶段卷积在每个层中单独排序,而不是跨所有层进行全局排序,而且由于冗余识别阶段在每一层中选择了不同数量的卷积,该方法是一种层自适应方法
建立冗余图:
为了说明如何为卷积层构建一个图,我们使用 X X X 来表示某一层 W ( i ) W^{(i)} W(i) 的卷积的权重
我们首先展开(就是flatten操作)和标准化卷积的权重,将它们的长度更改为 1 1 1
这样的话 X X X 就可以看做是变成了 R n \mathbb{R}^n Rn 空间中 n n n 维单位球体的一个有限子集 S n = { x ∈ R n : ∣ x ∣ = 1 } \mathbb{S}^n=\{x\in\mathbb{R}^n:|x|=1\} Sn={x∈Rn:∣x∣=1}
因此假设 X X X 中的元素是不同的,我们可以将 X X X 上的图定义如下:
我们选取正实数 γ > 0 \gamma>0 γ>0,并将 X X X 上的边集定义如下:
E = { ( x , y ) ∈ X × X ? Δ : ∣ x ? y ∣ / b ≤ γ } E=\{(x,y)\in X×X \setminus\Delta :|x-y|/\sqrt{b}\le\gamma\} E={(x,y)∈X×X?Δ:∣x?y∣/b?≤γ}
其中 Δ = { ( x , x ) : x ∈ X } \Delta=\{(x,x):x\in X\} Δ={(x,x):x∈X} 是 X X X 的对角, ∣ x ? y ∣ |x-y| ∣x?y∣ 是 R n \mathbb{R}^n Rn 上的欧氏距离
这样我们就得到了图 ( X , E ) (X,E) (X,E)
根据定义 ( x , y ) ∈ E (x,y)∈E (x,y)∈E, 如果 γ γ γ 很小,意味着 x x x 和 y y y 近似相等
? ? ? 覆盖数:
我们上面的定义表示 ( X , d ) (X,d) (X,d) 是一个度量空间,其中 d d d 是之前定义的图的一个度量
假设 ? > 0 ?>0 ?>0 是一个固定的自然数,子集 X 0 ? X X_0\subset X X0??X 被称作 X X X 的 ? ? ? 覆盖数,如果 X ? ? { B ( x ‘ , ? ) : x ‘ ∈ X 0 } X\subset\bigcup\{B(x`,?):x`\in X_0\} X??{B(x‘,?):x‘∈X0?}
其中 B ( x ‘ , ? ) = { x ∈ X : d ( x ‘ , x ) ≤ ? } B(x`,?)=\{x\in X:d(x`,x)\le ?\} B(x‘,?)={x∈X:d(x‘,x)≤?} 是一个以 x ‘ x` x‘ 为中心的半径为 ? ? ? 的球体
这表示 X X X 是由球 KaTeX parse error: Expected 'EOF', got '}' at position 20: …x`,?):x`\in X_0}? 覆盖
我们称以下数量为 X X X 的 ? ? ? 覆盖数:
N ? c ( X ) = m i n { # X 0 : X 0 ? i s ? a n ? ? ? c o v e r ? s e t ? o f ? X } N^c_?(X)=min\{\#X_0:X_0 \space is\space an\space?-cover\space set\space of\space X\} N?c?(X)=min{#X0?:X0??is?an???cover?set?of?X}
图的分解:
图中我们定义等价关系 x ~ y x\sim y x~y 当且仅当 x x x 到 y y y 存在路径
假设 X / ~ = { X 1 , X 2 , 。 。 。 , X k } X/\sim=\{X_1,X_2,。。。,X_k\} X/~={X1?,X2?,。。。,Xk?} 是商数空间
这个数学概念意味着:使用等价关系,我们可以将集合 X X X 分解为一个不相交的并集 X = X 1 ∪ X 2 ∪ ? ? ? ∪ X k X=X_1∪X_2∪···∪X_k X=X1?∪X2?∪???∪Xk?,使同一 X i X_i Xi? 中的元素是等价的
因此我们称数字 k k k(等价类的总数)为商空间的大小
直观地说 k k k 就是 ( X , E ) (X,E) (X,E) 的未连接子图的数量
图的冗余:
直观地说,商空间大小和 ? ? ? 覆盖数越大,表明一组数据越复杂,也就是冗余较少
事实上, x ∈ B ( x ‘ , ? ) x∈B(x‘,?) x∈B(x‘,?) 当且仅当 d ( x , x ’ ) ≤ ? d(x,x’)≤? d(x,x’)≤?,因此 x x x 和 x ‘ x‘ x‘ 近似相等
因此, ? ? ? 覆盖数可以近似地看作是 X X X 中线性无关的向量的总数
在论文的实现中,作者简单地使用了 ? = 1 ?=1 ?=1,因为同时考虑了性能和计算效率
基于上述分析,我们就可以定义图(也就是模型中对应的层)冗余:
R ( X ) = N w 1 k + w 2 N 1 c R(X)=\frac{N}{w_1k+w_2N^c_1} R(X)=w1?k+w2?N1c?N?
其中 { w 1 , w 2 } \{w1,w2\} {w1,w2} 是平衡 k k k 和 N 1 c N_1^c N1c? 的重要性的概率权值, N N N 是卷积的数量
1-覆盖面数的估值:
由于 ? ? ? 覆盖数的计算是 N P NP NP问题,因此作者提出了一种轻量级的方法来估计 N 1 c N_1^c N1c?
假设 X 0 X_0 X0? 是图 X X X 的 1-覆盖集,因此 # X 0 = N 1 c \#X_0=N_1^c #X0?=N1c?
我们通过如下方式估计 # X 0 \#X_0 #X0? 的值:
我们取固定的 ? ? ? ( 1 1 1或 2 2 2),假设 x 1 ( ? ) ∈ X x^{(?)}_1\in X x1(?)?∈X,满足 d e g ( x 1 ( ? ) ) = m a x { d e g ( x ) : x ∈ X } deg(x^{(?)}_1)=max\{deg(x):x\in X\} deg(x1(?)?)=max{deg(x):x∈X}
我们定义一个优先序列 { x 1 ( ? ) , x 2 ( ? ) , . . . , x n ? ( ? ) } \{x^{(?)}_1,x^{(?)}_2,...,x^{(?)}_{n?}\} {x1(?)?,x2(?)?,...,xn?(?)?} 如下:
如果我们定义了 x k ( ? ) x^{(?)}_k xk(?)? 那么只有两种可能的情况:(1) X = ? i = 1 k B ( x k ( ? ) , ? ) X=\bigcup_{i=1}^kB(x^{(?)}_k,?) X=?i=1k?B(xk(?)?,?),也就是说球 { B ( x k ( ? ) , ? ) : 1 ≤ i ≤ k } \{B(x^{(?)}_k,?):1\le i\le k\} {B(xk(?)?,?):1≤i≤k} 的族是 X X X 的 ? ? ?-覆盖集,这样我们就可以停止构造这个序列;(2)否则选取 x k + 1 ( ? ) ∈ X ? ? i = 1 k B ( x k ( ? ) , ? ) x^{(?)}_{k+1}\in X\setminus\bigcup_{i=1}^kB(x^{(?)}_k,?) xk+1(?)?∈X??i=1k?B(xk(?)?,?) 加入序列,满足:
d e g ( x k + 1 ( ? ) ) = m a x { d e g ( x ) : x ∈ X ? ? i = 1 k B ( x k ( ? ) , ? ) } deg(x^{(?)}_{k+1})=max\{deg(x):x\in X\setminus\bigcup_{i=1}^kB(x^{(?)}_k,?)\} deg(xk+1(?)?)=max{deg(x):x∈X??i=1k?B(xk(?)?,?)}
我们重复上面的过程,并最终得到序列:
{ x 1 ( ? ) , x 2 ( ? ) , . . . , x n ? ( ? ) } , \{x^{(?)}_1,x^{(?)}_2,...,x^{(?)}_{n?}\}, {x1(?)?,x2(?)?,...,xn?(?)?}, ? = 1 ? o r ? 2 ?=1\space or \space2 ?=1?or?2
很明显我们有 N 1 c = # X 0 ≤ n 1 N_1^c=\#X_0\le n_1 N1c?=#X0?≤n1?,因为族 { B ( x k ( 1 ) , 1 ) : 1 ≤ k ≤ n 1 } \{B(x^{(1)}_k,1):1\le k\le n_1\} {B(xk(1)?,1):1≤k≤n1?}
而且对于任意 i ≠ j ( i , j ≤ n 2 ) i\ne j(i,j\le n_2) i?=j(i,j≤n2?),我们有: d ( x i ( 2 ) , x j ( 2 ) ) ≥ 3 d(x_i^{(2)},x_j^{(2)})\ge 3 d(xi(2)?,xj(2)?)≥3
另一方面,对于每一个 x 0 ∈ X 0 x_0∈X_0 x0?∈X0? 和任意 x , y ∈ B ( x 0 , 1 ) x,y∈B(x_0,1) x,y∈B(x0?,1),我们有 d ( x , y ) ≤ d ( x , x 0 ) + d ( x 0 , y ) ≤ 2 d(x,y)≤d(x,x_0)+d(x_0,y)≤2 d(x,y)≤d(x,x0?)+d(x0?,y)≤2
回想一下, X 0 X_0 X0?是 X X X 的 1 1 1-覆盖的子集,然后对于任何 x i ( 2 ) x^{(2)}_i xi(2)?,存在(可能不是唯一的) x 0 ∈ X 0 x_0∈X_0 x0?∈X0? ,这样就有 x i ( 2 ) ∈ B ( x 0 , 1 ) x^{(2)}_i∈B(x_0,1) xi(2)?∈B(x0?,1)
此外,对于 i ≠ j i\ne j i?=j, x i ( 2 ) x^{(2)}_i xi(2)? 和 x j ( 2 ) x^{(2)}_j xj(2)? 不能在同一个球 B ( x , 1 ) B(x,1) B(x,1) 中,否则会产生 d ( x i ( 2 ) , x j ( 2 ) ) ≤ 2 d(x^{(2)}_i,x^{(2)}_j)≤2 d(xi(2)?,xj(2)?)≤2(矛盾)
我们看到 n 2 ≤ # X 0 = N 1 c n_2≤\#X_0=N^c_1 n2?≤#X0?=N1c?,因此有: n 2 ≤ N 1 c ≤ n 1 n_2≤N^c_1≤n_1 n2?≤N1c?≤n1?
因此如果 ∣ n 1 ? n 2 ∣ |n1-n2| ∣n1?n2∣ 足够下,我们就可以使用 N ~ 1 c = 1 2 ( n 1 + n 2 ) \tilde{N}^c_1=\frac{1}{2}(n_1+n_2) N~1c?=21?(n1?+n2?) 来估计 N 1 c N_1^c N1c?
虽然我们从理论上找不到它的上界,但在各种网络上的大量实验表明, N ~ 1 c \tilde{N}^c_1 N~1c? 作为对 N 1 c N_1^c N1c? 的估计已经足够好了,而且 N ~ 1 c \tilde{N}^c_1 N~1c? 的计算开销非常小
卷积选择策略:
在识别了具有大冗余的层之后,我们从这些层中删除了不重要的卷积
我们可以通过随机初始化从头开始训练一个修剪过后的网络架构,也可以从预先训练过的网络中删除某些卷积并进行微调
在作者的研究中,作者使用了一个非常常见和简单的策略,即用较小的绝对权值裁剪卷积
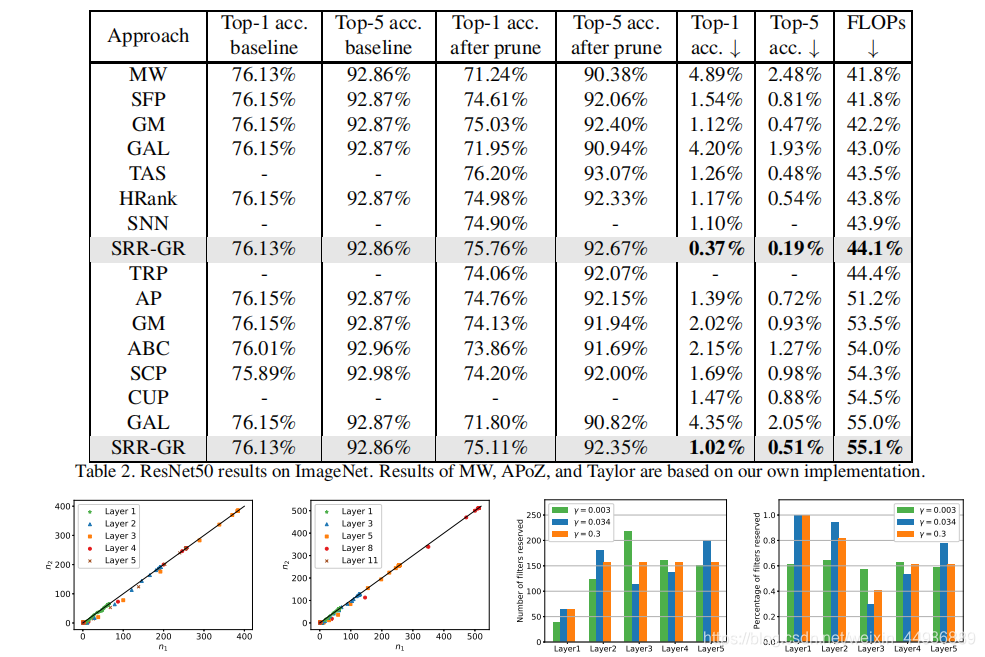
实验结果:
联系作者:
微信号:Sharpiless
作者的其他主页:
AI Studio:https://aistudio.baidu.com/aistudio/personalcenter/thirdview/67156
我的公众号:
