[数据结构与算法]反 转 链 表

首先是单链表的构建

struct ListNode {
	int val;
	ListNode* next;
	ListNode(int x) :val(x) { }
};

反转整个链表 Easy

（力扣206. 反转链表）难度：Easy

递归写法

ListNode* Reverse(ListNode* head) {
	if (head->next == nullptr) {	//当前节点是最后一个
		return head;
	}
	ListNode* last = reverse(head->next);
	head->next->next = head;
	head->next = nullptr;
	return last;
}

递归不要试着跳进递归，而是去了解函数的意义

比如我reverse函数的意义就是传入一个head节点，将head结点后面的链表全部反转，并返回反转之后的头结点

当前的链表是这个样子，当调用reverse(head->next)之后

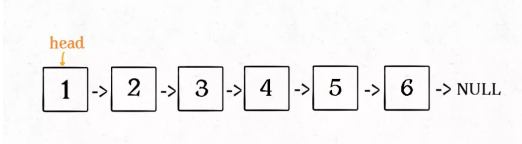
? 就应该是这个样子，并且返回1结点后面的链表反转之后的头结点

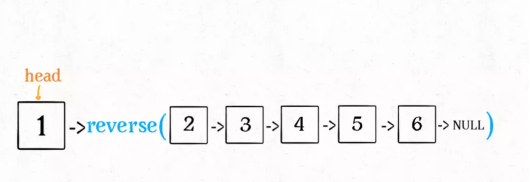
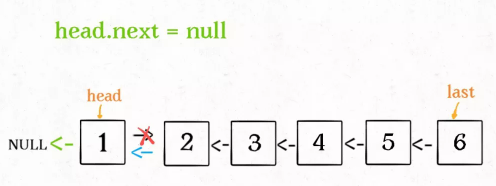
? 那么当后面的链表反转之后，应该是如下图，此时返回的结点应该是6这个结点

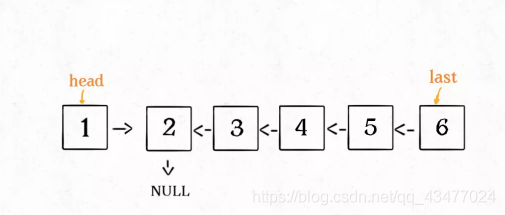
? head->next->next = head;的意义显而易见

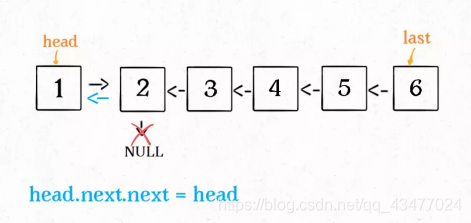
然后便是

head->next = nullptr;
return last;

迭代写法

ListNode* Reverse(ListNode* head) {
	if (head == nullptr) {
		return nullptr;
	}
	ListNode* pre = nullptr;
	while (head) {
		ListNode* temp = head->next;
		head->next = pre;
		pre = head;
		head = temp;
	}
	return pre;
}

反转前N个链表结点

ListNode* preNode = nullptr;
ListNode* ReverseN(ListNode* head, int n) {
	if (head == nullptr) {
		return nullptr;
	}
	if (n == 1) {
		//记录n+1个结点
		preNode = head->next;
		return head;
	}
	// 以 head.next 为起点，需要反转前 n - 1 个节点
	ListNode* last = ReverseN(head->next, n - 1);

	head->next->next = head;
	// 让反转之后的 head 节点和后面的节点连起来
	head->next = preNode;
	return last;
}

反转[m,n]区间的链表 Midium

（力扣92. 反转链表 II）难度：Midium

ListNode* preNode = nullptr;
ListNode* ReverseN(ListNode* head, int n) {
	if (head == nullptr) {
		return nullptr;
	}
	if (n == 1) {
		//记录n+1个结点
		preNode = head->next;
		return head;
	}
	// 以 head.next 为起点，需要反转前 n - 1 个节点
	ListNode* last = ReverseN(head->next, n - 1);

	head->next->next = head;
	// 让反转之后的 head 节点和后面的节点连起来
	head->next = preNode;
	return last;
}

ListNode* ReverseMToN(ListNode* head, int m, int n) {
	if (head == nullptr) {
		return nullptr;
	}
	if (m == 1) {
		return ReverseN(head, n);
	}
	head->next = ReverseMToN(head->next, m - 1, n - 1);
	return head;
}

k个一组反转链表 Hard

（力扣 25. K 个一组翻转链表 ）难度 ：Hard

ListNode* Reverse(ListNode* a, ListNode* b) {	//反转[a,b]区间的链表
	ListNode* pre, * cur, * nxt;
	pre = nullptr, cur = a, nxt = b;
	while (cur != b) {
		nxt = cur->next;
		cur->next = pre;
		pre = cur;
		cur = nxt;
	}
	return pre;
}

ListNode* ReverseKGroup(ListNode* head, int k) {
	if (head == nullptr) {
		return nullptr;
	}
	ListNode* a, * b;
	a = b = head;
	for (int i = 0; i < k; ++i) {
		if (b == nullptr)
			return head;
		b = b->next;
	}
	ListNode* newHead = Reverse(a, b);
	a->next = ReverseKGroup(b, k);
	return newHead;
}