对于大厂面试而言,01背包主要考察两种背包:
1、01背包
n种物品,每种物品只有一个
2、 完全背包
n种物品,每种物品无限个
3、 多重背包
n种物品,每种物品个数各不相同
LeetCode上面没有纯粹的01背包问题,主要是背包问题的应用
下面给出一个简单的01背包问题的例子
| 重量 | 价值 | |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
其中,背包最大重量为4,可装满的最大价值为?
(1)考虑暴力解法
每个物品两个状态:取or不取
因此我们可以用?回溯算法 来枚举所有情况;时间复杂度O(2^n)【这个就涉及到学习回溯算法咯】
(2)二维dp数组解法
动态规划五部曲:
1、明确dp数组含义
????????dp[i][j] :0 ~ i?之间的物品任取,放进容量为?j?的背包里的最大价值
2、确定递推公式
? ? ? ? 思考:dp[i][j] 可由哪些状态推导而来?此题中,有两种状态:放物品i or 不放物品i
? ? ? ? 若不放——dp[i - 1][j]
? ? ? ? 放物品i——dp[i - 1][j - weight[i]] + value[i]
? ? ? ? 我们的目的是求最大价值,因此需要在两种状态中取其大者,即:
? ? ? ? dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
? ? ? ? 上述即为递推公式
3、dp数组的初始化
? ? ? ? 首先,为了方便分析问题,我们可以先画出二维的dp数组矩阵
| 背包容量 | |||||
| dp[i][j] | 0 | 1 | 2 | 3 | 4 |
| 物品0 | 0 | 15 | 15 | 15 | 15 |
| 物品1 | 0 | ||||
| 物品2 | 0 | ||||
? ? ? ? 我们需要初始化什么呢?这个需要具体情况具体分析
? ? ? ? 在该例中,对于第一列,在背包容量为0的情况下,无法放入任何物品。因此该列可全部初始化为0;对于第一行,在该状态下只有物品0可以选取,那么满足物品0重量的背包状态,皆需要初始化为物品0的value;而对于小于物品0重量的背包状态,无法放入物品0,因此初始化为0。至此,二维dp数组的初始化完成。
? ? ? ? 问题:在上述初始化完成后,其他的位置该如何进行初始化?
? ? ? ? 很多人都默认初始化为0。运行可通过,但是我们需要思考我们该如何初始化其他位置?其实本题中,初始化为什么都可以。因为下面的每个状态,都是由我们上述的初始化推导而来的,并不受其他因素影响(比如该位置初始值与其他状态的比较)
4、确定遍历顺序
? ? ? ? 我们通常都知道,一般都是两个for循环来完成遍历。但是,两个for循环分别都是什么含义呢?第一层遍历物品还是背包容量?这个问题不可马虎,需要仔细考虑。对于此题,for循环的次序可以进行颠倒。只要左上方和正上方有数值,就不影响数组推导。
5、举例推导dp数组
| 背包容量 | |||||
| dp[i][j] | 0 | 1 | 2 | 3 | 4 |
| 物品0 | 0 | 15 | 15 | 15 | 15 |
| 物品1 | 0 | 15 | 15 | 20 | 35 |
| 物品2 | 0 | 15 | 15 | 20 | 35 |
?二维dp数组代码实现
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int Package01(const vector<int>& weight, const vector<int>& value, int bagWeight) {
//定义dp数组,行为物品,列为背包容量
vector<vector<int>> dp(weight.size(), vector<int>(bagWeight + 1, 0));
//初始化dp数组
//1、由于数组已经全部初始化为0,因此无需再初始化列
//2、初始化行
for (int k = 0; k <= bagWeight; ++k) {
if (k >= weight[0])
dp[0][k] = value[0];
else
continue;
}
//打印dp数组初始化行
for (int i = 0; i <= bagWeight; ++i)
cout << dp[0][i] << ' ';
cout << endl;
//状态转移方程及动态规划
for (int i = 1; i < weight.size(); ++i) {
for (int j = 0; j <= bagWeight; ++j) {
if (j < weight[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
cout << dp[i][j] << ' ';
}
cout << endl;
}
return dp[weight.size() - 1][bagWeight];
}
int main() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
int ans = Package01(weight, value, bagWeight);
cout << ans << endl;
return 0;
}?结果为:
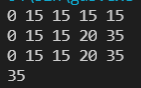
?符合推导的dp数组