文章目录
1. 树的基本结构
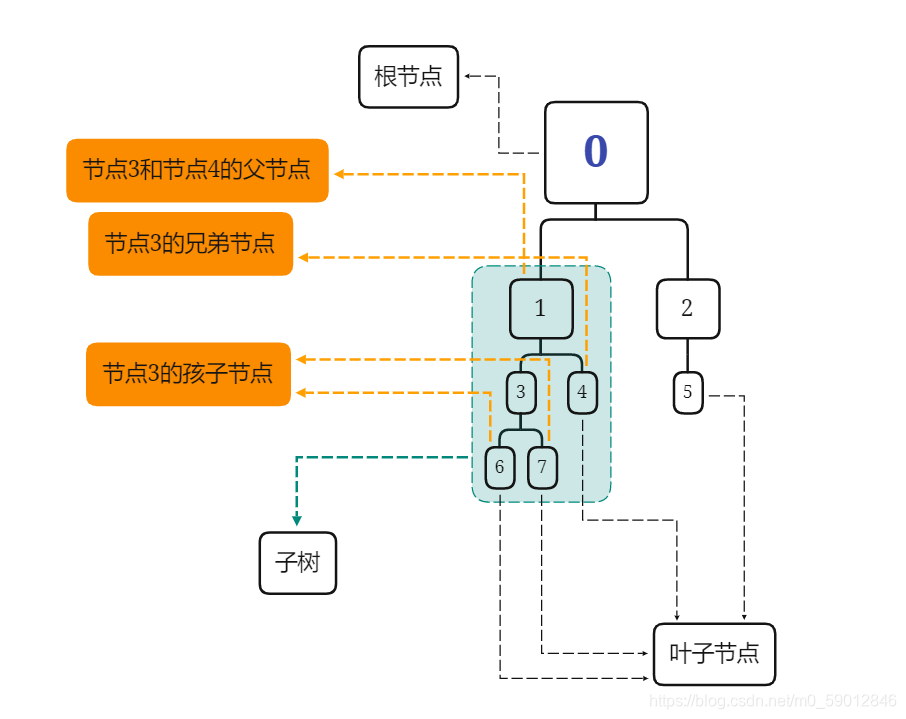
树是有n个节点的有限集。在任意的非空树中,树有且仅有一个特定的称为 根(root) 的节点,如节点 【0】。如果 n>1,其他的节点则可以分成 m 个互不相交的有限集,每一个都是一个树,是根的 子树,如下图的绿色区域。
以节点【3】为例,节点的上一级节点是 父节点(parent),如节点【1】。节点的下一级节点是 孩子节点(child),如节点【6】【7】。若有由同一个父节点衍生出来的节点,称为 兄弟节点(sibling),如节点【4】。节点【4】【5】【6】【7】是树的末端,没有孩子节点,称为 叶子节点(leaf)。
树的最大层级数称为树的 高度或深度,如该树的高度为4。
2. 二叉树 Binary Tree
2.1. 二叉树基本结构
二叉树是树的一种,它的限制是一个节点最多有 2 个子节点。左边的子节点叫 left child,右边的子节点叫 right child。
二叉树有两种特殊形态:
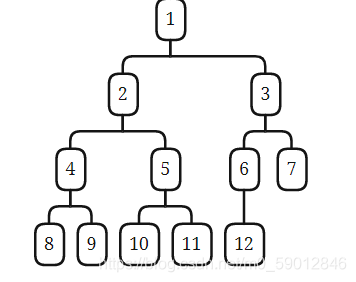
- 满二叉树:二叉树的所有非叶子节点都存在两个子节点,并且所有叶子节点在同一层级。

- 完全二叉树:一个有 n 个结点的二叉树,按层级顺序进行编号,编号为 1 到 n。满足这个树所有节点和同样深度的满二叉树的同编号节点位置相同。
2.2. 二叉树存储结构
2.2.1. 链式存储
链式存储本质是是对单链表的变形。单链表每个节点具有 data 变量和 next 指针构成。二叉树中,我们增加了一个指针,每个节点除了 data 变量外,还有 left 和 right 两个指针分别指向左、右两个子节点。
2.2.2. 数组存储
数组存储,需要把二叉树的节点按 层级顺序 放到数组中。如果某一节点的左、右子节点出现空缺,那我们必须在数组存放时相应的位置也空出来。这样存放的目的是可以通过计算下标直接定位二叉树的子节点和父节点位置。(例:父节点下标为1,左子节点下标为 2 * 1 + 1 = 3,右子节点下标为 2*1 + 2 = 4)
2.3. 二叉树的遍历
二叉树的遍历可以归结为两大类:深度优先遍历和广度优先遍历。其中深度优先遍历包括前序遍历,中序遍历,后序遍历。广度优先遍历包括层序遍历。
构架二叉树
class TreeNode(object):
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def create_binary_tree(input_list=[]):
""" 构建二叉树 """
if input_list is None or len(input_list) == 0:
return None
data = input_list.pop(0)
if data is None:
return None
node = TreeNode(data)
node.left = create_binary_tree(input_list)
node.right = create_binary_tree(input_list)
return node
2.3.1. 深度优先遍历
2.3.1.1. 前序遍历实现
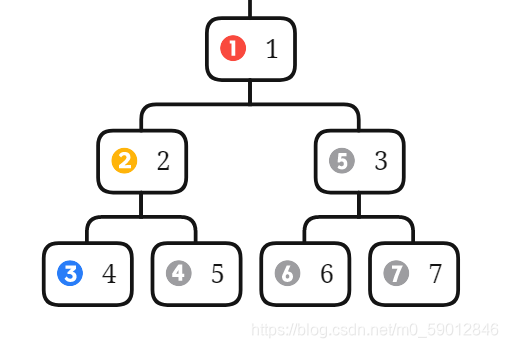
遍历顺序:根节点,左子树,右子树
- 递归
def pre_order_traversal(node):
""" 前序遍历 """
if node is None:
return
print(node.data)
pre_order_traversal(node.left)
pre_order_traversal(node.right)
return node
- 非递归(栈)
def pre_order_traversal_by_stack(node):
""" 前序遍历 """
stack = []
while(node is not None or len(stack) > 0):
while(node is not None):
print(node.data)
stack.append(node)
node = node.left
if len(stack)>0:
node = stack.pop()
node = node.right
2.3.1.2. 中序遍历实现
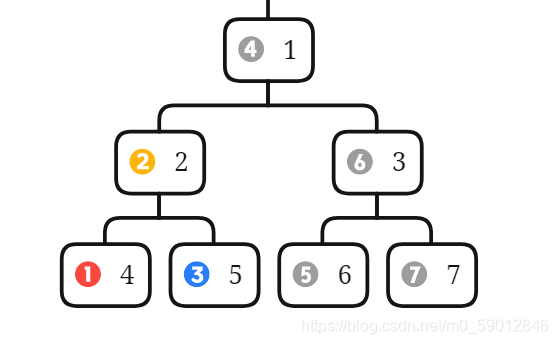
遍历顺序:左子树,根节点,右子树
- 递归
def in_order_traversal(node):
""" 中序遍历 """
if node is None:
return
in_order_traversal(node.left)
print(node.data)
in_order_traversal(node.right)
return node
- 非递归(栈)
def in_order_traversal_by_stack(node):
""" 中序遍历 """
stack = []
while(node is not None or len(stack) > 0):
while(node is not None):
stack.append(node)
node = node.left
if len(stack)>0:
node = stack.pop()
print(node.data)
node = node.right
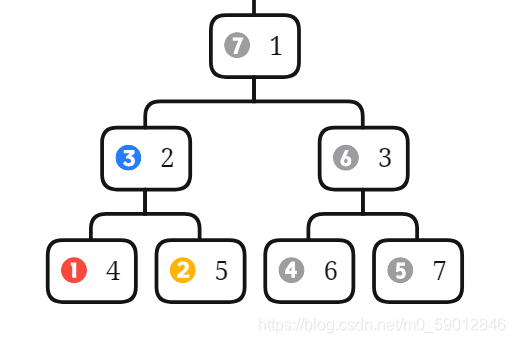
2.3.1.3. 后序遍历实现
遍历顺序:左子树,右子树,根节点
- 递归
def post_order_traversal(node):
""" 后序遍历 """
if node is None:
return
post_order_traversal(node.left)
post_order_traversal(node.right)
print(node.data)
return node
- 非递归(栈)
def post_order_traversal_by_stack(node):
""" 后序遍历 """
stack = []
parent = []
while(node is not None or len(stack) > 0):
while(node is not None):
stack.append(node)
node = node.left
if len(stack)>0:
node = stack.pop()
if node.right is None:
print(node.data)
if len(parent) > 0:
print(parent.pop().data)
else:
parent.append(node)
node = node.right
while(len(parent)>0):
print(parent.pop().data)
2.3.2. 广度优先遍历
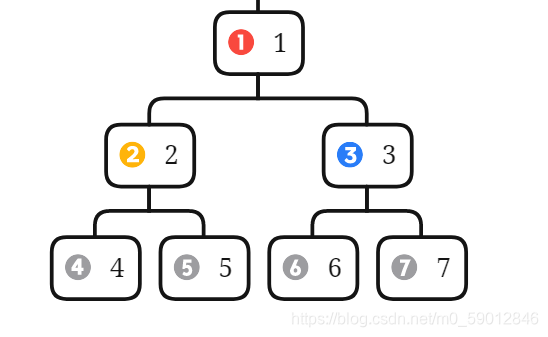
2.3.2.1. 层序遍历
遍历顺序:按照根节点到叶子节点的层次关系,一层一层横向遍历
- 递归
def level_order_traversal(node):
""" 层序遍历 """
# TODO
- 非递归(队列)
def level_order_traversal_by_queue(node):
""" 层序遍历 """
queue = Queue()
queue.put(node)
while(not queue.empty()):
node = queue.get()
print(node.data)
if node.left is not None:
queue.put(node.left)
if node.right is not None:
queue.put(node.right)
3. 二叉堆 Binary Heap
TODO