上面举了一个数字全排列的例子,再让我们来看leetcode017这题
题目:
https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
题解:
一:回溯算法解释的比较清楚
二:代码用了hashmap和我的思路差不多
解题历程:
自己写的(部分实现)
public static List<String> letterCombinations(String digits){
List<String> s=new ArrayList<>() ;//s用来存储字母组合
//建立一个哈希Map
HashMap<Integer, String> hashmap = new HashMap<>();
hashmap.put(2, "abc");
hashmap.put(3, "def");
hashmap.put(4, "ghi");
hashmap.put(5, "jkl");
hashmap.put(6, "mno");
hashmap.put(7, "pqrs");
hashmap.put(8, "tuv");
hashmap.put(9, "wxyz");
int len=digits.length();//输入字符串的长度
String [] n=new String[len];//建立一个字符串数组保存对应的字母组合
比如digits="234"--->n[]={"abc","def","ghi"};
for(Map.Entry<Integer,String> entry:hashmap.entrySet()) {
for (int i = 0; i < digits.length(); i++) {
int t= Integer.parseInt(Character.toString(digits.charAt(i)));
if (entry.getKey().equals(t)) {
n[i] = entry.getValue();
}
}
}//for
if(len<1) return s;
if(len==1) {
for (int i = 0; i < n[0].length(); i++) {
char temp = n[0].charAt(i);
String t = Character.toString(temp);
s.add(t);
}
}
for(int i=0;i<len-1;i++){
for(int j=0;j<n[i].length();j++){
for(int k=0;k<n[i+1].length();k++){
StringBuffer temp=new StringBuffer();
temp.append(n[i].charAt(j));
temp.append(n[i+1].charAt(k));
s.add(temp.toString());
}
}
}//for
return s;
}错误点总结:

这里由于我一直使用digtis=“23”这个例子,导致我一直以为temp只能是“ad”这样的两个字符。
后来提交后发现当digits=“234”,temp=“adg”这样子,我一下子就懵逼了,同时也发现了问题所在,就是我们没办法知道for循环的层数。也就导出了回溯这个神奇的方法。
回溯算法
地址:
1概念:
回溯法简单来说就是按照深度优先的顺序,穷举所有可能性的算法,但是回溯算法比暴力穷举法更高明的地方就是回溯算法可以随时判断当前状态是否符合问题的条件。一旦不符合条件,那么就退回到上一个状态,省去了继续往下探索的时间。
最基本的回溯法是在解空间中穷举所有的解。比如求序列[1,2,3]的全排列,那么我们可以画出一颗解空间树。
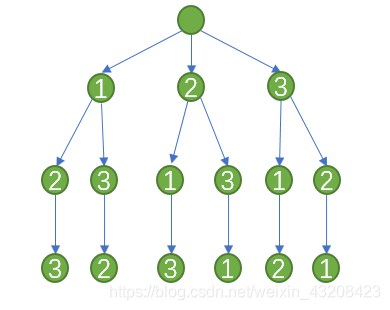
回溯法的特点是深度优先遍历,也就是该问题的遍历顺序是1->2->3,然后从子节点3返回,从子节点2返回,再到1->3->2,以此类推。
状态的返回只有当前的节点不再满足问题的条件或者我们已经找到了问题的一个解时,才会返回,否则会以深度优先一直在解空间树内遍历下去。
当然,对于某些问题如果其解空间过大,即使用回溯法进行计算也有很高的时间复杂度,因为回溯法会尝试解空间树中所有的分支。所以根据这类问题,我们有一些优化剪枝策略以及启发式搜索策略。
所谓优化剪枝策略,就是判断当前的分支树是否符合问题的条件,如果当前分支树不符合条件,那么就不再遍历这个分支里的所有路径。
所谓启发式搜索策略指的是,给回溯法搜索子节点的顺序设定一个优先级,从该子节点往下遍历更有可能找到问题的解。
2 回溯函数的组成
1.回溯出口,当找到了一个问题的解时,存储该解。
2.回溯主体,就是遍历当前的状态的所有子节点,并判断下一个状态是否是满足问题条件的,如果满足问题条件,那么进入下一个状态。
3.状态返回,如果当前状态不满足条件,那么返回到前一个状态。
def backtrack(current_statement) -> bool:
?? ?if condition is satisfy:
?? ??? ?solution = current_statement
?? ??? ?return True
?? ?else:
?? ??? ?for diff_posibility in current_statement:
?? ??? ??? ?next_statement = diff_posibility
?? ??? ??? ?if next_statement is satisfy condition:
?? ??? ??? ??? ?if backtrack(next_statement):
?? ??? ??? ??? ??? ?return True
?? ??? ??? ??? ?else:
?? ??? ??? ??? ??? ?back to current_statement
?? ??? ?return False
?
3 简单的回溯函数
3.1 问题描述
给定一个不包含重复数字的序列,返回所有不重复的全排列。
3.1.1 问题分析
遍历所有的解空间树即可找到答案。
首先定义一个回溯函数
# combination 为当前的状态
backtrack(combination=[])
那么它的出口部分也很好写,就是当combination的长度等于序列的长度时,就找到了问题的一个解。
if len(combination) == len(nums): answer.append(combination)
然后是回溯函数的主体部分,我们要遍历当前状态下的所有子节点,并判断子节点是否还符合问题的条件,那么对于这个问题,因为全排列的数是不能够重复的,所以我们的判断方式是当前的数没有包含在combination中,那么进入下一个状态。
for num in nums:
? ? if num not in combination:
? ? ? ? backtrack(combination+[num])
那么这个问题需要返回上一个状态吗?答案是不需要,因为backtrack的下一个状态的写法是backtrack(combination + [num]),这并不会改变我们当前的combination的值,因为我们没有对combination对象进行一个重新的赋值操作。
如果说修改一下回溯函数的主体。
for num in nums:
? ? if num not in combination:
? ? ?? ?combination.append(num)
? ? ? ? backtrack(combination+[num])
那么这时候,combination的值被改变了,所以需要写一个返回上一个状态的代码。
for num in nums:
? if num not in combination:
? ? ? combination.append(num)
? ? ? backtrack(combination)
? ? ? combination.pop()
并且,因为我们传入的是相当于是combination对象,所以在存储解的时候需要深拷贝。
if combination.__len__() == nums.__len__():
? ? solution = copy.deepcopy(combination)
? ? answer.append(solution)
3.1.2 完整代码
import copy
class Solution:
? ? def permute(self, nums: list):
? ? ? ? answer = []
? ? ? ? def backtrack(combination=[]):
? ? ? ? ? ? if combination.__len__() == nums.__len__():
? ? ? ? ? ? ? ? solution = copy.deepcopy(combination)
? ? ? ? ? ? ? ? answer.append(solution)
? ? ? ? ? ? ? ? return
? ? ? ? ? ? for num in nums:
? ? ? ? ? ? ? ? if num not in combination:
? ? ? ? ? ? ? ? ? ? combination.append(num)
? ? ? ? ? ? ? ? ? ? backtrack(combination)
? ? ? ? ? ? ? ? ? ? combination.pop()
? ? ? ? backtrack()
? ? ? ? return answer
上面举了一个数字全排列的例子,再让我们来看leetcode017这题
具体思路:
这次是用了四层循环。现在是不是能看出一些门道了?对的。循环的嵌套层数,就是输入的字符串长度。输入的字符串长度是1,循环只有1层。
输入的字符串长度是3,循环就是3层。如果输入的字符串长度是10,那么循环就是10层。
可是输入的字符串长度是不固定的,对应的循环的嵌套层数也是不固定的,那这种情况怎么解决呢?这时候递归就派上用场了。
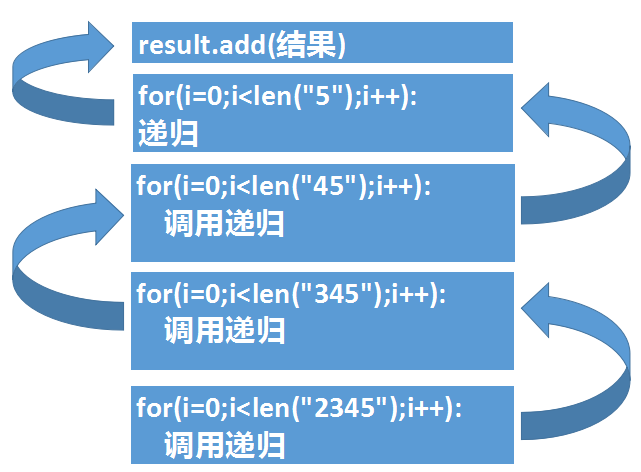
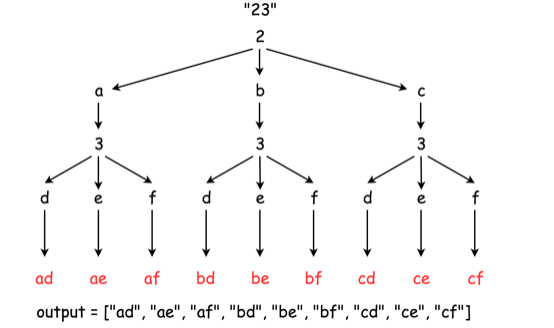
对于打印"2345"这样的字符串:
第一次递归就是上图中最下面的方格,然后处理完第一个字符2之后,将输入的字符改变成"345"并调用第二个递归函数
第二次递归处理3,将字符串改变成"45"后再次递归
第三次递归处理4,将字符串改变成"5"后继续递归
第四次递归处理5,将字符串改变成""后继续递归
最后发现字符串为空了,将结果放到列表中并返回
上面是从函数调用的角度去看的,而每次调用下一层递归时,都需要将本层的一些处理结果放到一个临时变量中,再传递给下一层,从这个变量层层传递的变化看,就像一棵树一样,这个算法的时间复杂度很高,是O(3^n)这个级别的,空间复杂度是O(n)
代码(解法一):
class Solution {
//一个映射表,第二个位置是"abc“,第三个位置是"def"。。。
//这里也可以用map,用数组可以更节省点内存
String[] letter_map = {" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
//特别注意的是由于输入键盘里面没有"0","1",而为了实现下标和数组字母一一对应的关系
//所以 letter_map[0]=" ",letter_map[1]="*",这里起到的其实是属于一种占位符的作用
public List<String> letterCombinations(String digits) {
//注意边界条件
if(digits==null || digits.length()==0) {
return new ArrayList<>();
}
iterStr(digits, new StringBuilder(), 0);
return res;
}
//最终输出结果的list
List<String> res = new ArrayList<>();
//递归函数
void iterStr(String str, StringBuilder letter, int index) {
//递归的终止条件,注意这里的终止条件看上去跟动态演示图有些不同,主要是做了点优化
//动态图中是每次截取字符串的一部分,"234",变成"23",再变成"3",最后变成"",这样性能不佳
//而用index记录每次遍历到字符串的位置,这样性能更好
if(index == str.length()) {
res.add(letter.toString());
return;
}
//获取index位置的字符,假设输入的字符是"234"
//第一次递归时index为0所以c=2,第二次index为1所以c=3,第三次c=4
//subString每次都会生成新的字符串,而index则是取当前的一个字符,所以效率更高一点
char c = str.charAt(index);
//map_string的下表是从0开始一直到9, c-'0'就可以取到相对的数组下标位置
//比如c=2时候,2-'0',获取下标为2,letter_map[2]就是"abc"
int pos = c - '0';
String map_string = letter_map[pos];
//遍历字符串,比如第一次得到的是2,也就是遍历"abc"
for(int i=0;i<map_string.length();i++) {
//调用下一层递归,用文字很难描述,请配合动态图理解
letter.append(map_string.charAt(i));
//如果是String类型做拼接效率会比较低
//iterStr(str, letter+map_string.charAt(i), index+1);
iterStr(str, letter, index+1);
//为什么要删除最后一个字符呢,是因为想让下一字符进来更替
//比如已经有一个组合“ad”,这时候我们就要将d删除,让e代替d的位置
letter.deleteCharAt(letter.length()-1);
}
}
}注意点:
这里有一个return的小知识点,当时不懂所以理解的时候很痛苦。
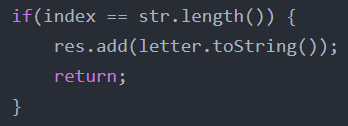
return: 从当前的方法中退出,返回到该调用的方法的语句处,继续执行,并不代表整个函数就停止了
代码(解法二):利用了hashmap
public List<String> letterCombinations(String digits) {
List<String> list = new ArrayList<>();
if (digits.length() == 0){
return list;
}
HashMap<Character,String> map = new HashMap();
map.put('2',"abc");
map.put('3',"def");
map.put('4',"ghi");
map.put('5',"jkl");
map.put('6',"mno");
map.put('7',"pqrs");
map.put('8',"tuv");
map.put('9',"wxyz");
back(list,map,digits,0,new StringBuffer());
return list;
}
public void back(List<String> list,HashMap<Character,String> map ,String digits,int index ,StringBuffer sb){
if (digits.length() == index ){
list.add(sb.toString());
return;
}
char first = digits.charAt(index);
String s = map.get(first);
for (int i = 0; i < s.length(); i++) {
char next = s.charAt(i);
sb.append(next);
back(list,map,digits,index+1,sb);
sb.deleteCharAt(index);
}
}