[数据结构与算法]Benelux Algorithm Programming Contest 2020 部分题解

B.Balanced Breakdown

• 题意
  给定一个整数$n$，需要你从中不断分离出回文数，使得$n$最后变成$0$，问需要最少的操作数，并输出方案。

• 解题思路
  我们肯定是贪心构造当前$n$能分离的最大回文数，那么如何构建呢？我们知道，对于回文数，其翻转过来和原来的数是相同的，则说明是回文数。我们可以截取$n$的一半，那么再对其左半端减$1$，就能保证右半段无论取什么构造出来的数都比$n$小，然后倒过来累加右半段即可，具体看代码。

• AC代码

/**
  *@filename:B
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-31 00:35
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 100000 + 5;
const int P = 1e9+7;

ll n;
vector<ll> result;
ll cal(ll n){
    if(n >= 11 && n <= 99)return n / 11 * 11;
    string s = to_string(n);
    string half = s;
    reverse(half.begin(),half.end());
    if(s == half)return n;
    if(stoll(half) == 1){
        return n - 1;
    }
    half = s.substr(0, s.size() + 1 >> 1);
    half = to_string(stoll(half) - 1); //将左半端取出来减1.
    string ans = half;
    int st = half.size() - 1 - s.size() % 2;
    for(int i = st; i >= 0; -- i){
        ans += half[i];
    }
    return stoll(ans);
}
void solve(){
    while(n){
        ll m = cal(n);
        //cout << m << endl;
        result.push_back(m);
        n -= m;
    }
    cout << result.size() << endl;
    for(ll &x : result){
        cout << x << endl;
    }
}
int main(){
    cin >> n;
    solve();
    return 0;
}

C.Corrupted Contest

• 题意
  有$n$个人，然后$p$道题，$t_i$表示排名第$i$的人做完最后一题的时间，若做题排序顺序唯一，求出每个人的做题排序顺序。

• 解题思路
  我们知道，在同解题数的情况下，排名高的比排名低的时间要少。对于解题数为$0$的，它们的罚时为$0$。那么我们知道一点，如果做题顺序是唯一的，那么第一名一定解决了所有的题，否则从解决了第一个题到第一个都可以往前推一个档次，所以我们可以直接从做题数$p$开始构造。
  那么需要注意的就是，相邻两个人的做题数不能跨度超过$1$，因为超过了也不能唯一确定。同时，如果最后一名的做题数不为$0$，同样需要检测是否超过了$2$，否则就可以通过做题数都减$1$构造一个排序了。

• AC代码

/**
  *@filename:C
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-30 16:12
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 10000 + 5;
const int P = 1e9+7;

int n,p;//n个团队，m个题目。
bool flag;//判断是否可以唯一确定。
int t[N],ans[N];//t[i]表示第i个团队的解题时间。ans[i]表示其解决了多少个问题。
void solve(){
    for(int i = 1; i <= n; ++ i){
        if(t[i] != 0 && p == 0){
            flag = true;
        }
        if(t[i] == 0){
            //罚时为0，说明没有解决问题。
            ans[i] = p = 0;
        }
        else if(t[i] >= t[i - 1]){
            ans[i] = p;
        }
        else{
            p --;
            ans[i] = p;
        }
        if(p < 0)flag = true;
        //解决从2突然跳到0的结果。
        if(ans[i - 1] - ans[i] > 1){
            flag = true;
        }
    }
    if(flag || (ans[n] > 1 && t[n] != 0)){
        printf("ambiguous\n");
    }
    else{
        for(int i = 1; i <= n; ++ i){
            printf("%d%c\n", ans[i], i == n ? '\n' : ' ');
        }
    }
}
int main(){
    scanf("%d%d", &n, &p); 
    for(int i = 1; i <= n; ++ i){
        scanf("%d", &t[i]);
    }
    solve();
    return 0;
}

D.Efficiently Elevated

• 题意

• 解题思路
  我们知道，对于楼层高度低于$2$的是可以直接到达不用电梯的。而对于高于$1$的楼层我们需要设置电梯，那么怎么设置呢，由于只能到达同一高度的楼层，所以我们肯定是先设计低楼层的，因为低楼层可以到达高楼层，高楼层到达不了低楼层，那么我们直接用$dfs$检索一下连通块即可。存储楼层高度大小可用优先队列实现，也可以自己排序。

• AC代码

/**
  *@filename:D
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-30 16:51
**/
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
const int N = 500 + 5;
const int P = 1e9+7;

struct node{
    int x,y,z;
    //注意自定义优先队列排序的一些细节。
    bool operator < (const node &A) const {
        return z < A.z;
    }
}nodes[N];
int n,m;//网格的高度和宽度。
bool p[N][N];//判断(i,j)是否已经被确定。
priority_queue<node> q;
int a[N][N];
int go[4][2] = {0,1,0,-1,1,0,-1,0};
void dfs(int x,int y){
    p[x][y] = 1;
    for(int i = 0; i < 4; ++ i){
        int dx = x + go[i][0],dy = y + go[i][1];
        if(dx >= 1 && dx <= n && dy >= 1 && dy <= m && a[dx][dy] <= a[x][y] && !p[dx][dy]){
            dfs(dx,dy);
        }
    }
}
void solve(){
    int ans = 0;
    while(!q.empty()){
        node head = q.top();
        q.pop();
        if(!p[head.x][head.y]){
            //开始遍历。
            dfs(head.x,head.y);
            ans ++;
        }
    }
    printf("%d\n", ans);
}
int main(){
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++ i){
        for(int j = 1; j <= m; ++ j){
            scanf("%d", &a[i][j]);
            if(a[i][j] <= 1){
                p[i][j] = 1;
            }
            else{
                p[i][j] = 0;
                q.push({i,j,a[i][j]});
            }
        }
    }
    solve();
    return 0;
}

F.Generator Grid

• 题意
  给你$n$个城市，然后给出$m$个可以建立发电站的城市，同时你可以建立电力线通过发电站城市连通相邻城市，问使所有城市发电的最小代价。

• 解题思路
  我们可以将点权转化为边权，即将发电站的点设为$n+1$，可以建立发电站设立为与城市的关系，那么答案就是使得$n+1$个点连通即可。利用Kruskal算法你。

• AC代码

/**
  *@filename:F
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-30 15:23
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 200000 + 5;
const int P = 1e9+7;

//点权转边权。
struct edge{
    int u,v,w;
    bool operator < (const edge &A){
        return w < A.w;
    }
}edges[N];
int n,m,tot;//顶点数、发电站数量。
int father[N];
ll ans;
int find(int x){
    int r = x;
    while(father[r] != r){
        r = father[r];
    }
    int i = x,j;
    while(father[i] != r){
        j = father[i];
        father[i] = r;
        i = j;
    }
    return r;
}
void solve(){
    //对电线排序。
    sort(edges + 1,edges + 1 + tot);
    for(int i = 1; i <= n + 1; ++ i){
        father[i] = i;
    }
    for(int i = 1; i <= tot; ++ i){
        int fu = find(edges[i].u),fv = find(edges[i].v);
        if(fu == fv)continue;//说明已经相连了。
        father[fu] = father[fv];
        ans += edges[i].w;
    }
    printf("%lld\n", ans);
}
int main(){
    scanf("%d%d", &n, &m);
    int idx,w;
    for(int i = 0; i < m; ++ i){
        scanf("%d%d", &idx, &w);
        edges[++tot] = {idx,n + 1,w};//将发电站看成结点n + 1
    }
    for(int i = 1; i <= n; ++ i){
        //输入电力线的成本。
        scanf("%d", &edges[++tot].w);
        edges[tot].u = i;
        if(i < n){
            edges[tot].v = i + 1;
        }
        else{
            edges[tot].v = 1;
        }
    }
    solve();
    return 0;
}

G.Hungry Henk

• 题意
  给你$n$个菜谱，其中包含菜名，选择一个菜谱，其中的菜名小于等于20个字符。

• 解题思路
  直接遍历即可。

• AC代码

/**
  *@filename:G
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-30 14:35
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 100 + 5;
const int P = 1e9+7;

int n;
string s;
vector<string> g[N];
bool vis[N];
bool flag;
void solve(){
    int idx = 0;
    for(int i = 1; i <= n; ++ i){
        if(vis[i]){
            idx = i;
            break;
        }
    }
    cout << g[idx].size() << endl;
    for(auto &s : g[idx]){
        cout << s << endl;
    }
}
int main(){
    cin >> n;
    int x;
    for(int i = 1; i <= n; ++ i){
        cin >> x;
        flag = false;
        while(x -- ){
            cin >> s;
            if(s.size() > 20){
                flag = true;
            }
            g[i].push_back(s);
        }
        if(!flag){
            vis[i] = true;
        }
    }
    solve();
    return 0;
}

H.Incomplete Implementation

• 题意
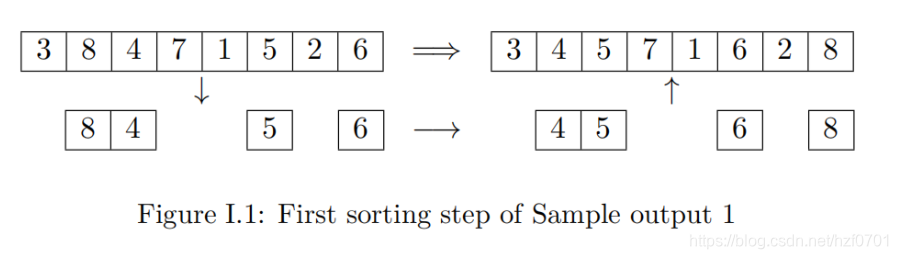
  给你$1$~$n$的排列数组，然后你可以每次任意选择n/2个不同的下标使得他们值排序，然后有序放回这几个位置，你最多有三次操作机请问你怎么操作，会使得这个乱序数组恢复有序。(可以输出仍以方式)
  

• 解题思路
  先排$[n/4?3+1,n]$区间，再排$n/4?2+1,n/4?3]$区间，然后再排$[1,n/2]$区间即可。怎么排呢？我们可以去寻找所在位置，然后利用原来位置和应该在的位置进行一次排序即可。

• AC代码

/**
  *@filename:H
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-30 17:23
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 100000 + 5;
const int P = 1e9+7;

int n,a[N],b[N];
int pos[N],vis[N];
void print(){
    int cnt = 0;
    for(int i = 1; i <= n; ++ i){
        if(vis[i])cnt ++;
    }
    for(int i = 1; i <= n && cnt < n / 2; ++ i){
        if(!vis[i]){
            vis[i] = true;
            cnt ++;
        }
    }
    int sz = 0;
    for(int i = 1; i <= n; ++ i){
        if(vis[i]){
            printf("%d ",i);
            b[++ sz] = a[i];
        }
    }
    sort(b + 1, b + sz + 1);
    sz = 0;
    for(int i = 1; i <= n; ++ i){
        if(vis[i])a[i] = b[++ sz];
        pos[a[i]] = i;
    }
    printf("\n");
    memset(vis,false,sizeof(vis));
}
void solve(){
    printf("3\n");
    for(int i = n / 4 * 3 + 1; i <= n; ++ i){
        vis[pos[i]] = true;
        vis[i] = true;
    }
    print();
    for(int i = n / 4 * 2 + 1; i <= n / 4 * 3; ++ i){
        vis[pos[i]] = true;
        vis[i] = true;
    }
    print();
    for(int i = 1; i <= n / 2; ++ i){
        vis[i] = true;
    }
    print();
}
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i){
        scanf("%d", &a[i]);
        pos[a[i]] = i;//记录a[i]的位置。
    }
    solve();
    return 0;
}

I.Jigsaw

• 题意
  给你$c$个对角块，$e$个边缘块，$m$个中心块，问你能否拼成一个矩形。

• 解题思路
  既然是对角，则必须满足$c\mathrm{m}\mathrm{o}\mathrm{d}4=0$，同时，由于有$e$个边缘块，需要分成$2$个长和宽，即$e\mathrm{m}\mathrm{o}\mathrm{d}2=0$，满足和这些条件之后，我们来假设去除对角和边缘形成的中间矩形长宽分别为$a,b$，那么满足：
  $(a+b)\times 2=e$
  $ab=m$
  利用等式代换得到一元二次方程求解再测试解的合法性即可解决此题。

• AC代码

/**
  *@filename:I
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-30 14:46
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 100000 + 5;
const int P = 1e9+7;

int c,e,m;
void solve(){
    if(c != 4 || e % 4 != 0){
        cout << "impossible" << endl;
        return;
    }
    //(a + b) * 2 = e
    //a * b = m;
    int a1,a2,b1,b2;
    //2a^2 - ea + 2m = 0;
    //利用求根公式。
    a1 = (e + sqrt(1.0 * e * e - 16.0 * m)) / 4;
    a2 = (e - sqrt(1.0 * e * e - 16.0 * m)) / 4;
    b1 = e / 2 - a1;
    b2 = e / 2 - a2;
    if(a1 * b1 == m){
        cout << a1 + 2 << " " << b1 + 2 << endl;
    }
    else if(a2 * b2 == m){
        cout << a2 + 2 << " " << b2 + 2 << endl;
    }
    else{
        cout << "impossible" << endl;
    }
}
int main(){
    cin >> c >> e >> m;
    solve();
    return 0;
}