在排序数组中查找元素的第一个和最后一个位置

分析:
??二分查找:一旦查找到target,就从该位置开始向两边扩张,找到边界。
代码:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size() == 0) {
return {-1, -1};
}
if(nums.size() == 1 && nums[0] == target) {
return {0, 0};
}
int n = nums.size();
int l = 0, r = n - 1;
while(l <= r) {
int mid = l + (r - l) / 2;
if(nums[mid] == target) {
int i = mid, j = mid;
while(i >= 0 && nums[i] == target) {
i--;
}
while(j < n && nums[j] == target) {
j++;
}
return {i + 1, j - 1};
}else if(nums[mid] > target) {
r = mid - 1;
}else {
l = mid + 1;
}
}
return {-1, -1};
}
};
组合总和
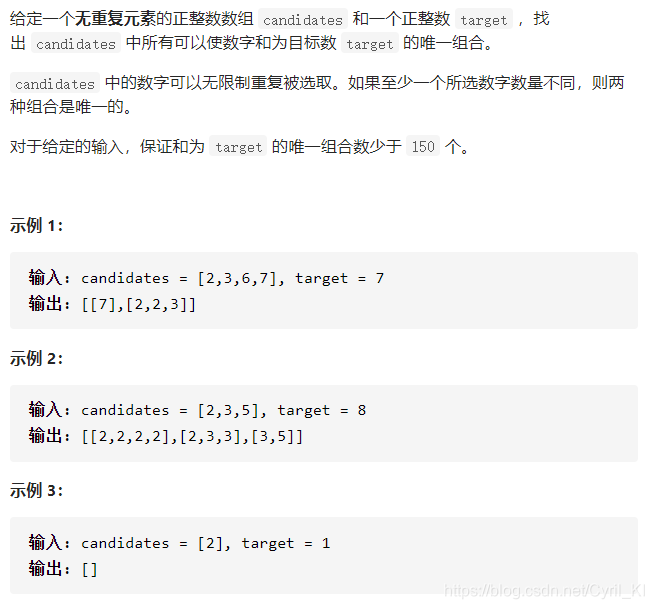
分析:
??dfs+回溯:每次可以选择跳过当前位置,也可以重复选择当前位置。
代码:
class Solution {
public:
void dfs(vector<int>& candidates, int target, vector<vector<int>>& res, vector<int>& cur, int ind) {
if(ind == candidates.size()) {
return;
}
if(target == 0) {
res.push_back(cur);
return;
}
dfs(candidates, target, res, cur, ind + 1);
if(target - candidates[ind] >= 0) {
cur.push_back(candidates[ind]);
target -= candidates[ind];
dfs(candidates, target, res, cur, ind);
target += candidates[ind];
cur.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> res;
vector<int> cur;
dfs(candidates, target, res, cur, 0);
return res;
}
};
全排列
旋转图像
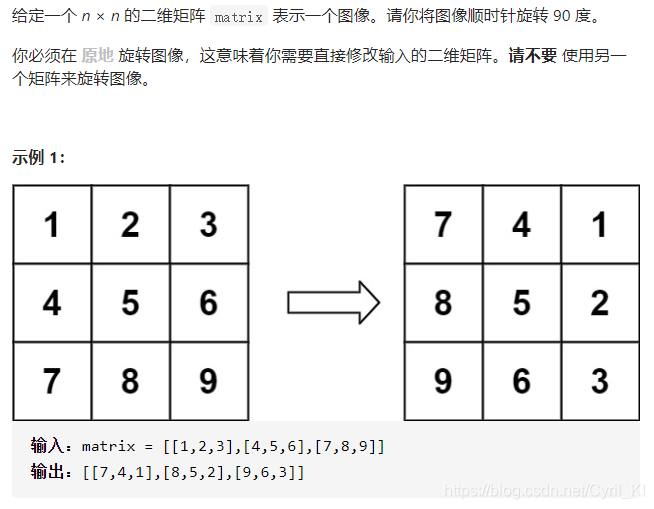
分析:
??原数组中的(row, col)旋转后,在新数组中的位置为(col, n - row - 1)。
代码:
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
vector<vector<int>> temp(n, vector<int>(n));
for(int row = 0; row < n; row++) {
for(int col = 0; col < n; col++) {
temp[col][n - row - 1] = matrix[row][col];
}
}
for(int row = 0; row < n; row++) {
for(int col = 0; col < n; col++) {
matrix[row][col] = temp[row][col];
}
}
}
};
字母异位词分组

分析:
??对原字符串数组中的每一个字符串进行排序,如果两个字符串是字母异位词,则排序后二者相同。基于这种性质,可以使用哈希表进行存储。
代码:
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
vector<vector<string>> res;
if(strs.size() == 0) {
res.push_back({});
res[0].push_back("");
return res;
}
//排序+哈希表
unordered_map<string, vector<string>> mp;
vector<string> temp;
for(int i = 0; i < strs.size(); i++) {
if(strs[i] == "") {
mp[""].push_back("");
continue;
}
string s = strs[i];
sort(s.begin(), s.end());
mp[s].push_back(strs[i]);
}
unordered_map<string, vector<string>>::iterator it = mp.begin();
for(; it != mp.end(); ++it) {
res.push_back(it->second);
}
return res;
}
};
跳跃游戏

分析:
??贪心算法:

代码:
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
int rightmost = 0;
for(int i = 0; i < n; i++) {
if(i <= rightmost) {
rightmost = max(rightmost, i + nums[i]);
if(rightmost >= n - 1) {
return true;
}
}
}
return false;
}
};
合并区间
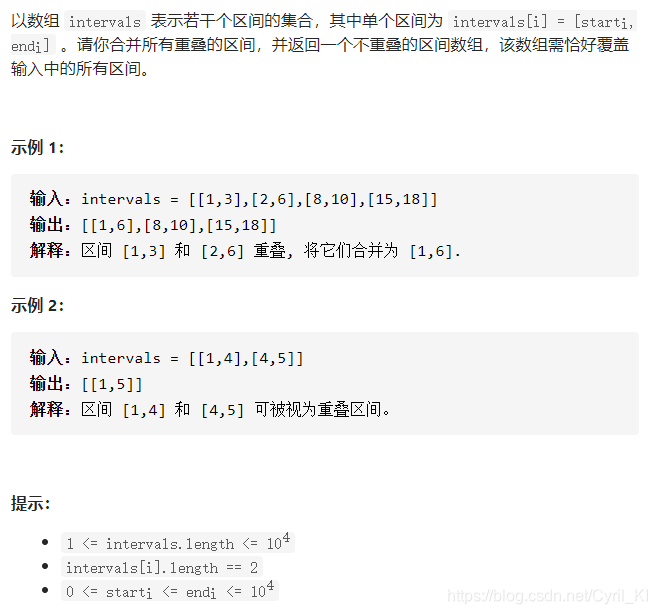
分析:
??将原数组按照左边界升序的原则进行排序,排序后可合并的区间一定是连续的。令结果数组为res,遍历排序后的数组,如果当前res为空,那么应该将当前区间加入;如果res中最后一个区间的右边界小于当前区间的左边界,那么当前区间显然是不能和res中最后一个区间合并的,单独加入;否则就能合并,由于是按照左边界升序排列,所以只需要将res中最后一个区间的右边界进行更新即可。
代码:
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> res;
sort(intervals.begin(), intervals.end());
int n = intervals.size();
for(int i = 0; i < n; i++) {
if(res.size() == 0 || res.back()[1] < intervals[i][0]) {
res.push_back(intervals[i]);
}else {
res.back()[1] = max(res.back()[1], intervals[i][1]);
}
}
return res;
}
};