堆结构非常重要

完全二叉树:或者是满的,在不满的最后一层也是从左往右依次变满的。
堆逻辑上就是完全二叉树
把数组必须从零出发的连续一段可以对应成完全二叉树
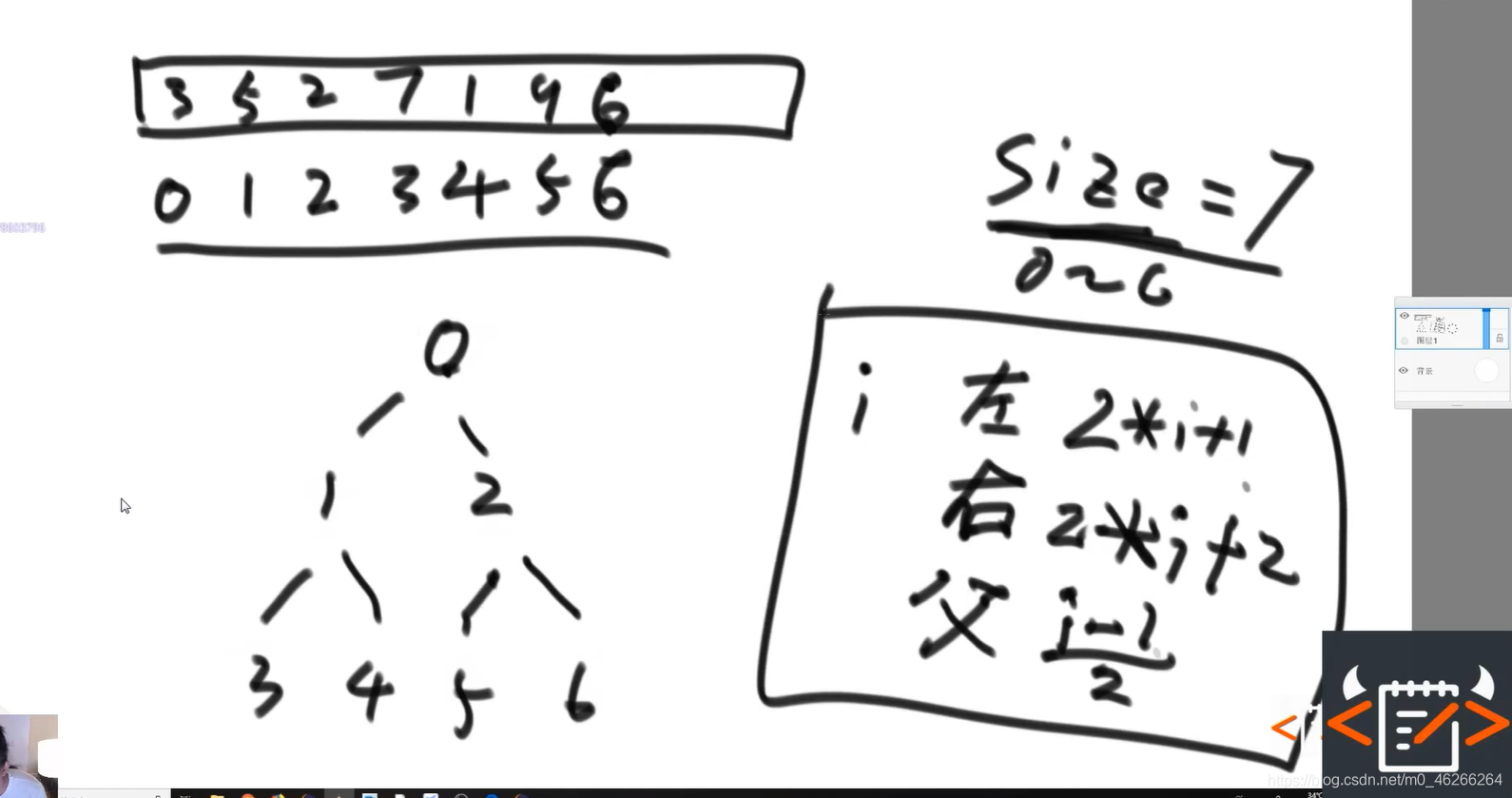
堆分为大根堆和小根堆
大根堆就是要求完全二叉树的每一颗子树最大值就是头结点的值
小根堆就是要求完全二叉树的每一颗子树最小值就是头结点的值
heapsize就是堆大小
heapify(堆化,非常重要的方法,从一个位置出发往下动保证堆结构):
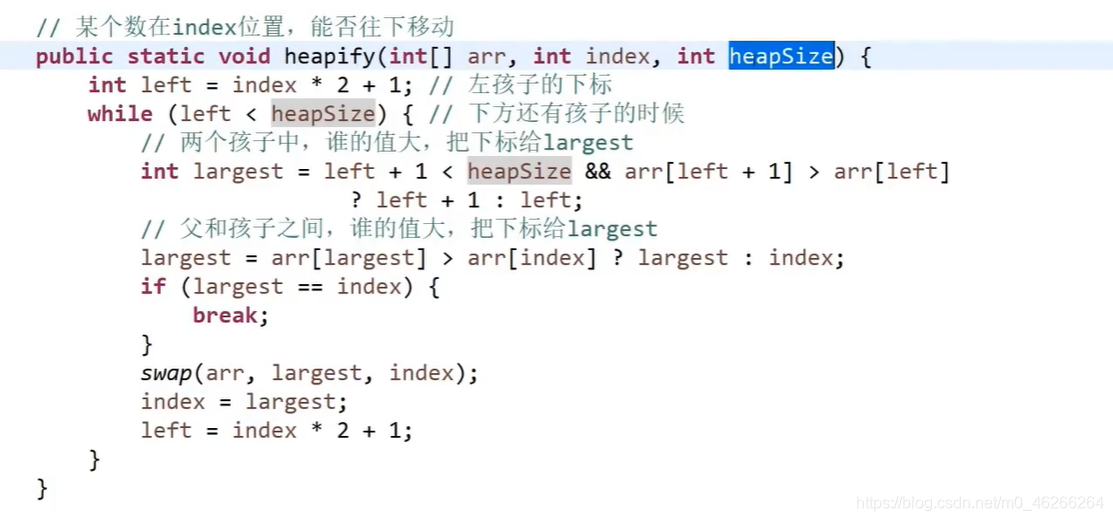
void heapify(int* arr, int index, int heapsize)
{
//index指是从哪个位置开始往下做heapify
// heapsize管着左右两个孩子,看是否越界
/由heapsize管着堆的大小
// 一旦发现左孩子的下标越界 ,说明我就没孩子
int left = 2*index + 1; //左孩子下标
while(left < heapsize) //下方还有孩子的时候
{
//两个孩子中,谁的值大,下标给largest
if(left + 1 < heapsize)//存在右孩子
{
//两个孩子中,谁的值大,把下标给largest
int largest = arr[left+1] > arr[left] ? left+1:left;
}
//父和较大子孩子之间,大的值赋给largest
largest = arr[largest] > arr[index] ? largest : index;
if(largest == index) break;//父节点最大
//largest != index 说明index是一定要往下走的,因为其较大孩子比它大
swap(arr, largest, index);
index = largest;
left = 2*index+1;
}
}
void heapInsert(int* arr, int index)
//某个数现在处在index位置,继续往上移动
//插入数字进入堆,保证堆仍然是大根堆
{
while(arr[index] > arr[(index-1)/2])//大于其父节点
{
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}

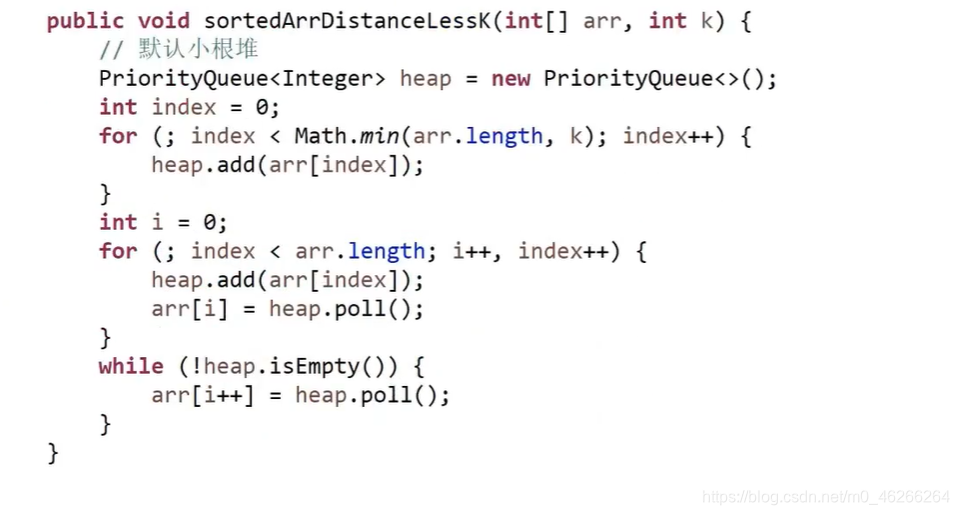
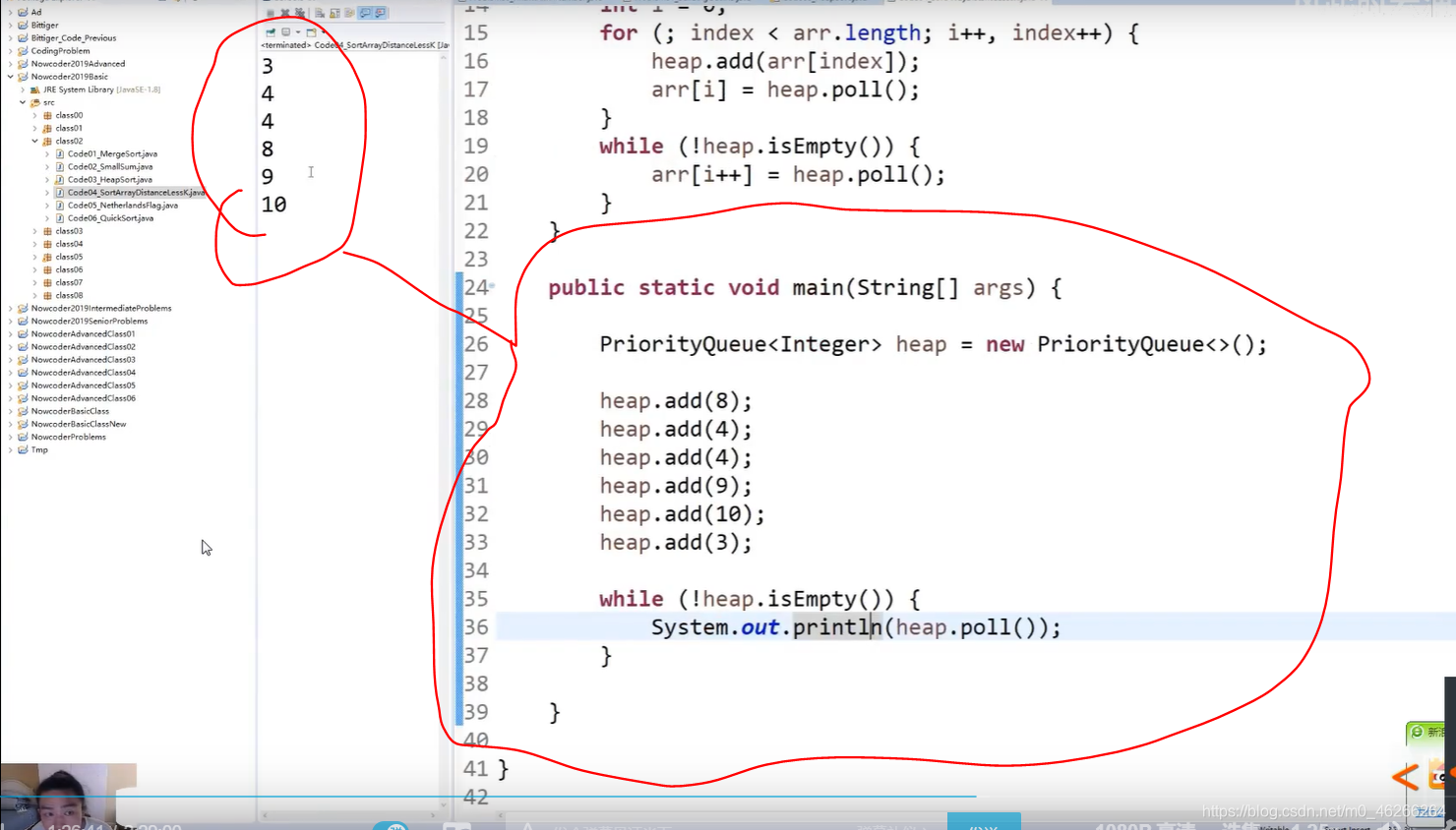
//小根堆其实就是优先级队列
//上面那道题就是优先级队列(底层就是堆,默认(即不传参数)小根堆)
//如下图,优先级队列弹出,小根堆,从小到大。
比较器

比较器就是告诉两个数怎么比大小,可以很好的优化代码
如下图,一个学生有名字,id,年龄,这些都是自己定义的结构,系统不知道怎么比大小。如果直接sort函数排序,会按照内存地址大小来排序,无意义。 但是如果有一个数组就不一样了,把它们三个组成一个数组,如下下图。

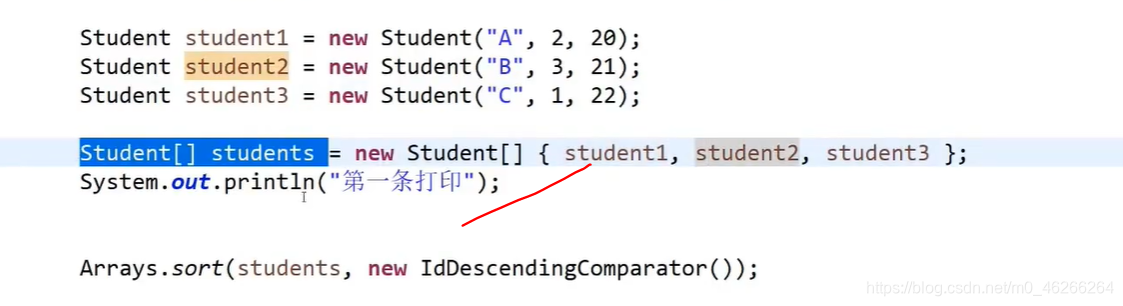
//ID升序比较器
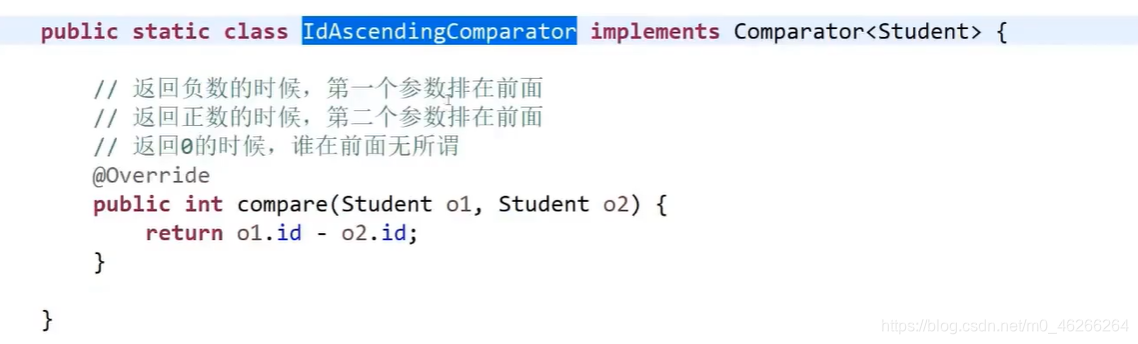
上图的注释,是所有比较器默认的规则
最后sort的时候把怎么比大小给它,把数组给它,OK了。
最后结果如下图
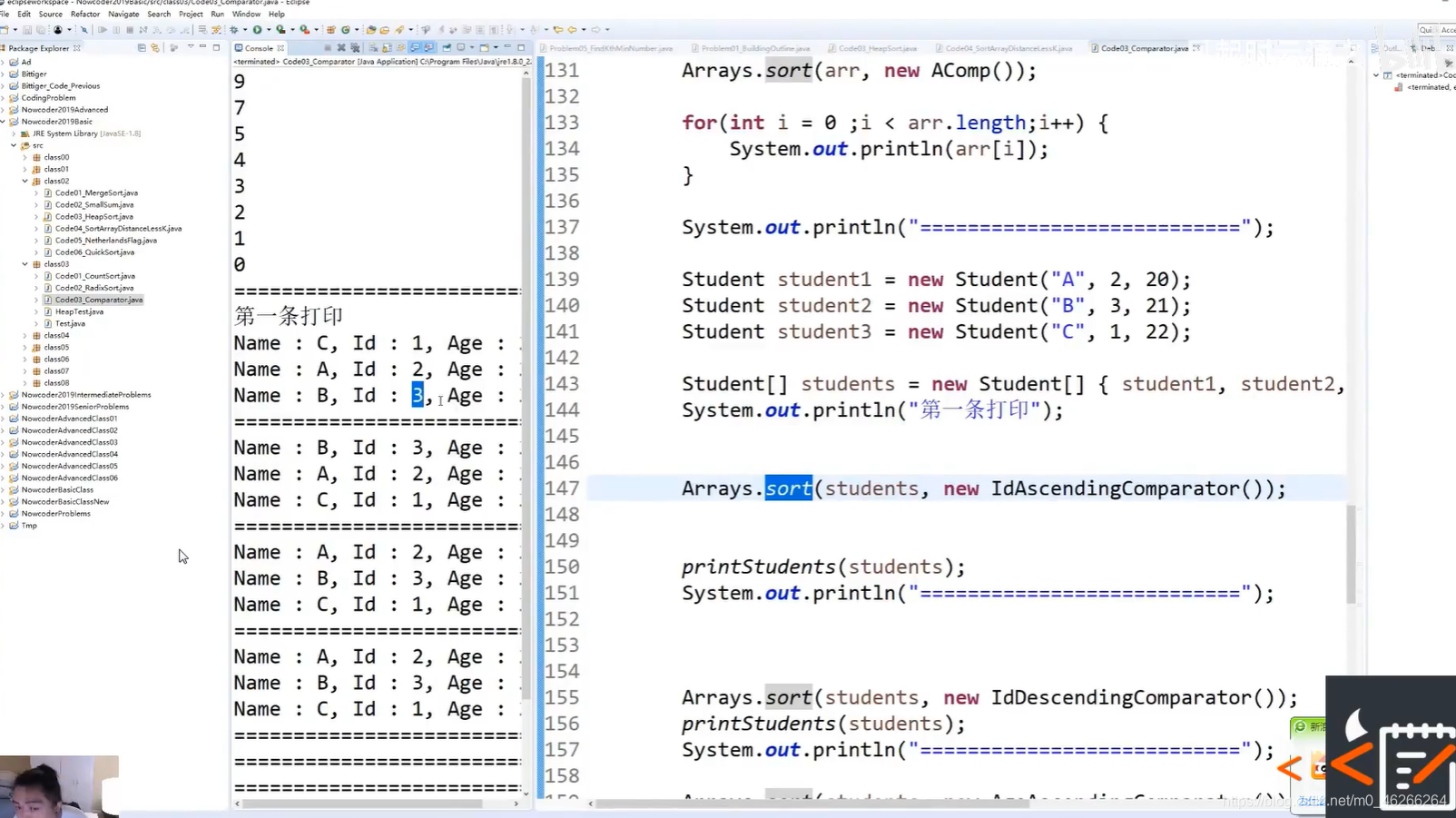
同理,年龄降序比较器,如下图
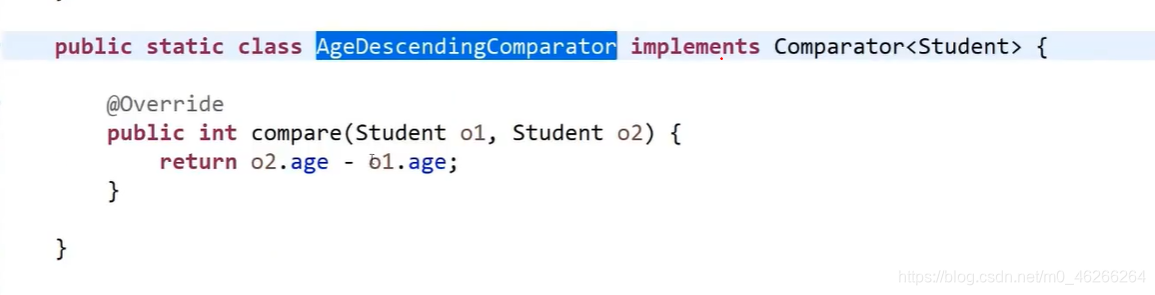
比较器在C++里面就叫重载比较运算符

稳定性就是,一个组数排序过后,值的等的数字的相对次序不变,则称这种排序算法稳定
int a[] = {1,8,3,8,7,3,3}
选择排序:
从下标0开始遍历,找出最小的放在位置0
从下标1开始遍历,找出第二小的放在1
明显选择排序不稳定
冒泡排序:排序n趟,每趟相邻两个数字比较,后面的数字小就和前面的交换,第一趟拍完以后可以保证最后一个是最大的。
可以稳定,遇到相同的数字不交换就行。
插入排序:
先保证0_0有序
0_1有序
0——2有序
0——3有序
0——4有序
可以稳定,遇到相同的数字不交换就行。
归并排序:先左边右边分别有序,再外排序,可以稳定
能用快排就用快排,快速排序时间复杂度最优
快排和堆排序是不稳定的

上图5:遇到这个题就是面试官在搞我。答:经典快速排序做不到稳定性,经典快排的ktion是0,1标准,和奇偶问题一个解,论文里stable sort里面有快排稳定算法,请解出。