
1. 理论基础
在图像的变换和卷绕中,我们已经建立了一个图片经过变换成为另一个图片的过程,事实上,我们在进行图像配准的时候,就是给出了两个图像,让我们判断图像之间的变换关系的过程。
如果图像A经过一些变换能得到图像B,我们只需要计算出这组变换,就可以得到图像的配准,并进行拼接。
所以,寻找图片中与所有匹配项最符合的变换T就是图像配准的过程。
最简单的例子就是平移
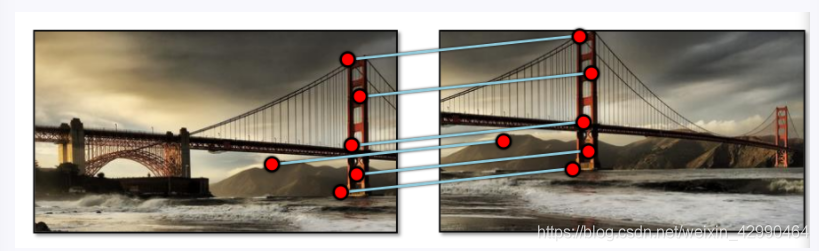
很明显,图片B中的特征点就是图片A中特征点平移的来的。所以,只需要计算出平移量(xt, yt),我们甚至可以将两个图像合成
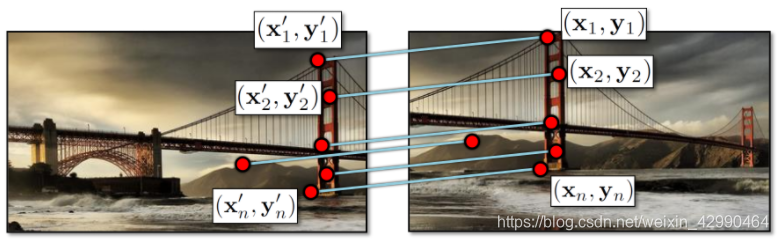
很明显,图片B中的特征点就是图片A中特征点平移的来的。所以,只需要计算出平移量(xt, yt),我们甚至可以将两个图像合成
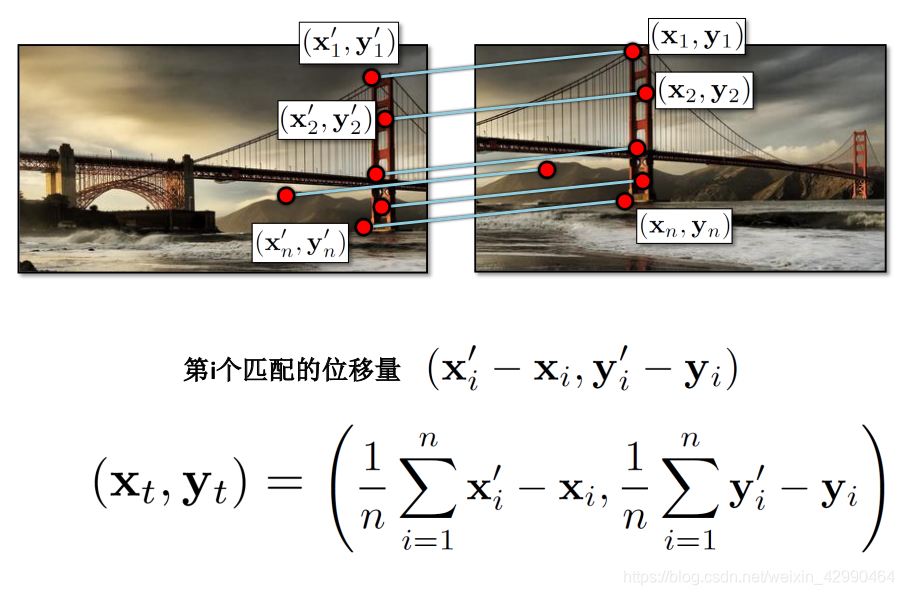
我们可以通过两个图片位置坐标的差值直接获得位移量,但是这十分不恰当(因为图片总不是完全匹配的)
所以,就如图中所说,使用所有匹配点的差值的均值是一个很好的方法。
2. 最小二乘法
对于仿射变换处理使用最小二乘法,这将很好的处理仿射变换,在平移问题,就相当于平均位移量。
2.1 从平移说起
对于一组平移图像,我们设其平移为(Xt,Yt)
对于一个点(Xi,Yi), 我们有
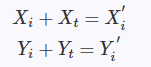
所以定义残差为
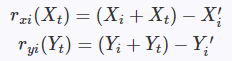
我们对于所有的匹配点求残差,这样,通过保证最小的残差平方和来求解(Xt,Yt)
为了保证平移向量(Xt,Yt)误差足够小,我们就需要保证他拥有最小的残差平方和:
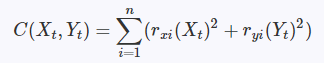
求解平移向量
对于这一过程,我们可以用矩阵表示

为了保证最小的残差平方和则|At?b|2要保证最小
为了求解t,我们就形成正则方程
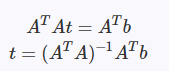
对于以上过程,需要注意的是,A是列满秩矩阵,否则,ATA逆矩阵是不存在的。
当然对于非列满秩矩阵,我们还有其他方法。
2.2 仿射变换
在图像的变换和卷绕时,我们就已经提到过仿射变换
具体的仿射变换矩阵是:
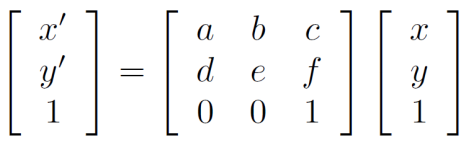
为了求解仿射变换矩阵,我们同样使用最小二乘法来求解问题,定义残差和代价函数,并且将其转换为矩阵形式求解。
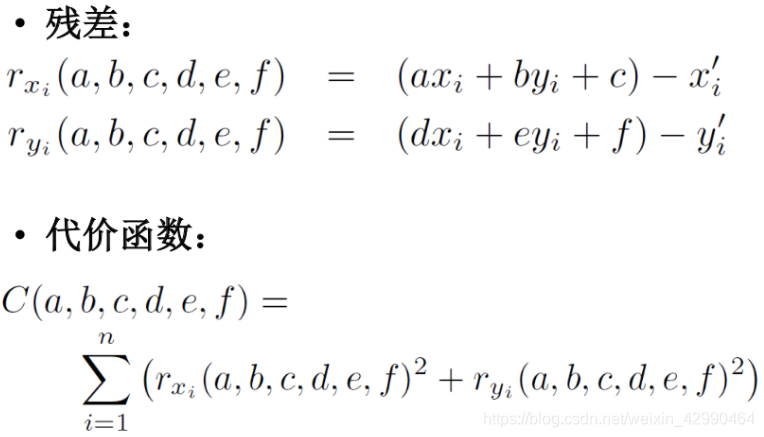

然后,我们就可以通过和平移一样的方法来求解t矩阵。
2.3 同态映射(Homographies)
同态映射的矩阵是:
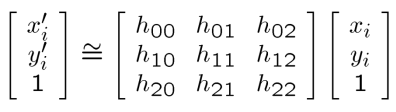
我们按照正常的操作将其展开可以得到
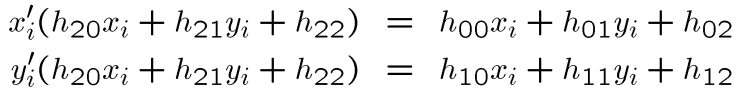
由于上式是非线性的,所以我们将矩阵设为:
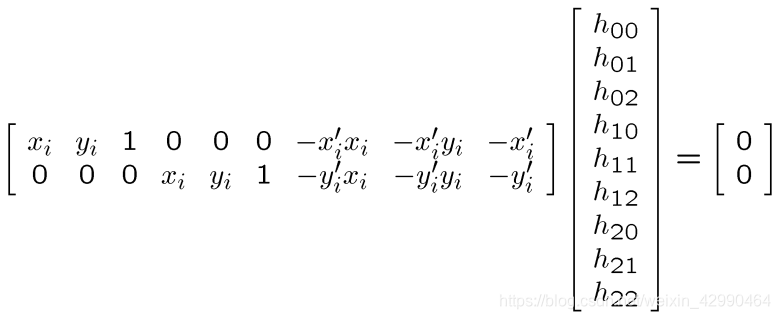
如果我们将这个参数扩展到xn,这时,我们就可以求解H矩阵了:

在上述的矩阵运算中即Ah=0:
- 因为h可缩放,因此限定问题的解h^为单位向量
- h^是ATA具有最小特征值的特征向量
- 需要四个或更多匹配点
2.4 总结
通过上述的内容,我们明白了如何给两个图像配准对齐。
假定给定图像A和B,我们需要三个步骤
- 计算A和B的图像特征
- 匹配A和B之间的特征
- 使用匹配集计算A到B同态映射矩阵的最小二乘解
3 RANSAC(随机抽样一致)
在图像匹配的时候,我们就知道,可能存在匹配不正确的点,也就是离群点(outliers)
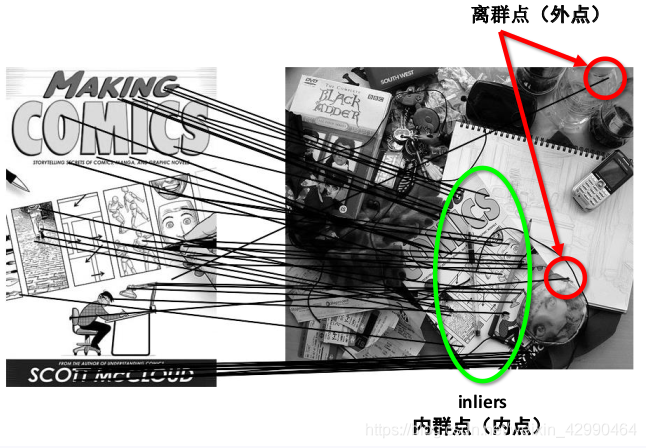
而最小二乘法会去适应包括局外点在内的所有点,比如当我们在平移时求解Xt时,我们拟合曲线
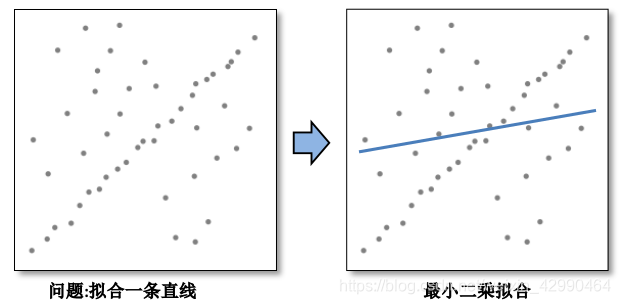
可以看出,拟合的曲线是尽量适配所有点的,所以其结果不太准确。而RANSAC能得出一个仅仅用局内点计算出模型,并且概率还足够高。
RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次数。
3.1 基本过程
- 随机选择S个样本,通常S是确定一个模型的最小样本数量。然后我们假设选取的样本全部是局内点
- 使用S个样本计算模型的一个解
- 用2求解出的一个模型计算其他所有数据,如果某个点适用于估计的模型,则认为是局内点。如果有足够多的局内点被归类为假设的局内点,则认为估计的模型足够合理
- 回到第一步,重复N次,并保留拥有最多局内点的模型。
- 然后重新使用所有的局内点去估计模型,因为它仅仅被初始的假设局内点估计过。
