[数据结构与算法]SPSS回归分析案例

SPSS回归分析案例

1.应用最小二乘法求经验回归方程

1.1数据导入

首先将数据导入SPSS如下：

1.2线性回归条件的验证

我们需要验证线性回归的前提条件：

• 线性（散点图，散点图矩阵）
• 独立性
• 正态性（回归分析的过程中可以检验）
• 方差齐性（回归分析的过程中可以检验）

1.2.1 散点图绘制

打开图形->旧对话框->散点/点状

选择矩阵分布后将X,Y作为变量绘制散点图：

最终得到散点图：

可以看出X-Y变量之间存在线性关系，下一步可以建立线性回归模型了。

1.3 线性回归模型的建立

在分析界面打开回归-线性，然后选择自变量和因变量进行分析，并在【统计量】中选择需要勾选的统计量。

其中：

• Dubin-Waston：独立性判断
• 共线性诊断：变量过多时可能某些变量之间存在线性关系，需要剔除或者选择公因子

然后我们在绘制选项中选择要绘制的图：

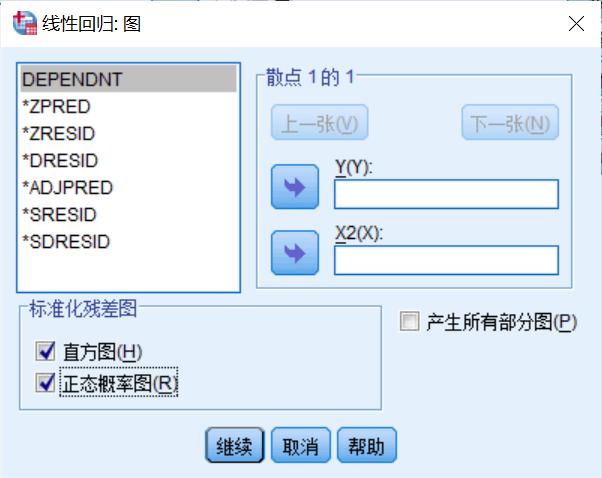
直方图和正态概率图：正态性检验

X和Y：方差齐性检验

最后我们点击确定可以得到导出的数据结果文件得到下面的结果

1.4结果分析

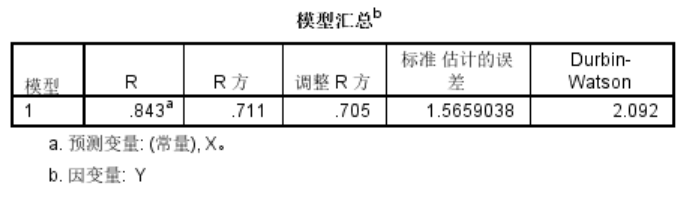
1.4.1 $R^2$和Durbin-Waston

$R^2$越接近1说明拟合程度越好，通常不能低于036，也就是R的绝对值不能小于0.6。

而对于独立性检验Durbin-Waston，值通常在0-4之间，越接近2独立性越好。

按照输出结果，线性回归在这两个指标下反映得很好：

1.4.2正态性检验

变量接近正态的，近似正态条件下即可作线性回归

1.4.3 回归方程和回归系数的检验

• 回归方程的显著性检验

其中的sig项表示回归方程存在的统计学意义

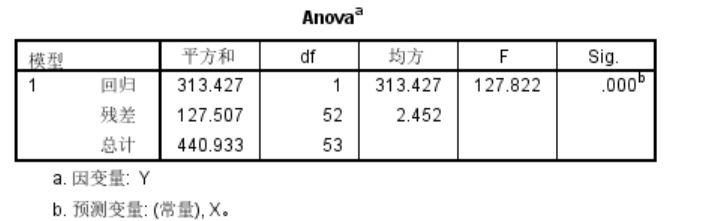
这里sig=0，即拒绝原假设，对应的回归系数不全为0。

• 回归系数的显著性检验

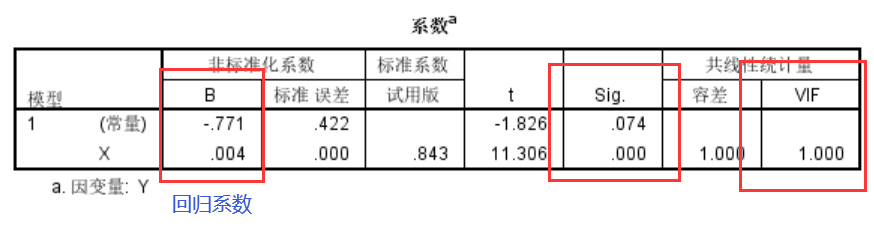
可得到线性回归方程为：
$$Y=0.04X?0.771$$
方差膨胀因子<10，说明数据不存在共线性问题。

2.Guass-Markov假设

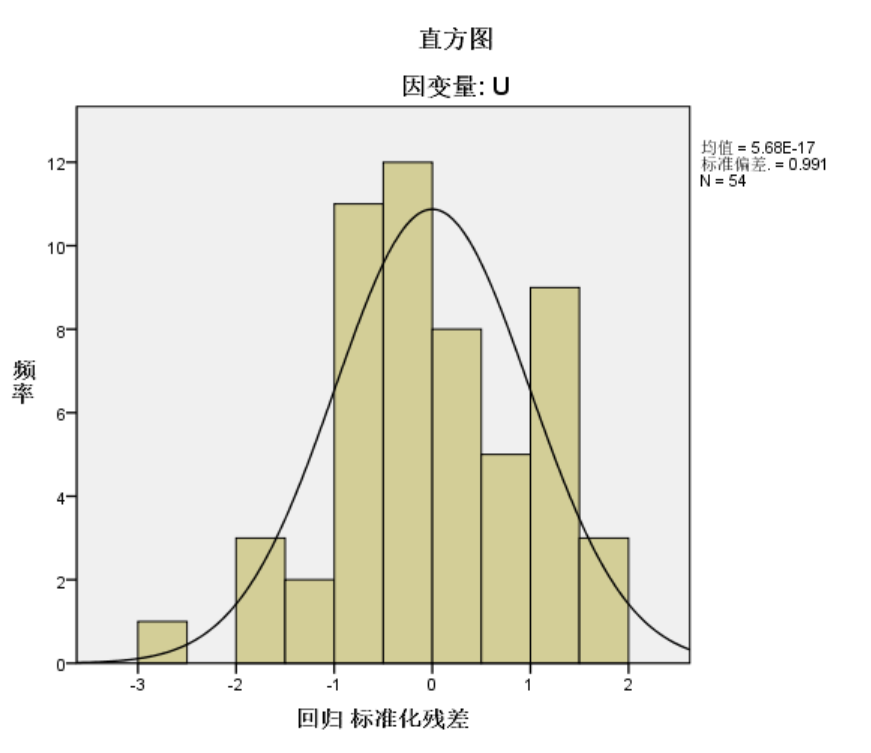
如下图可以看出残差基本分布在[-2,2]区间内，Guass-Markov假设在本例中是适用的。

3.考虑$U=Y^{\frac{1}{2}}$进行重做上述1和2

把U进行平方，进行$U^2$和X的回归分析即可。或者是下面直接对$U和X$做回归分析，得到下面结果：

在下面结果中，$R^2$没有低于最低下限。且由于是单变量，共线性等也不会存在问题。

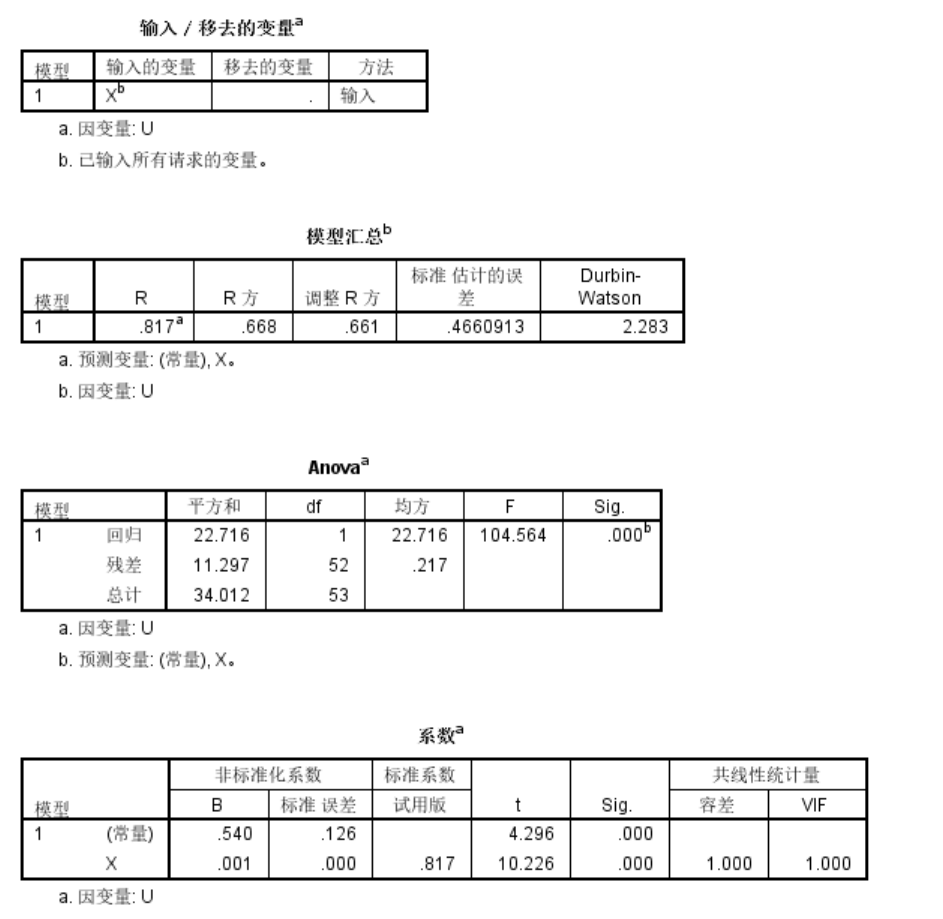
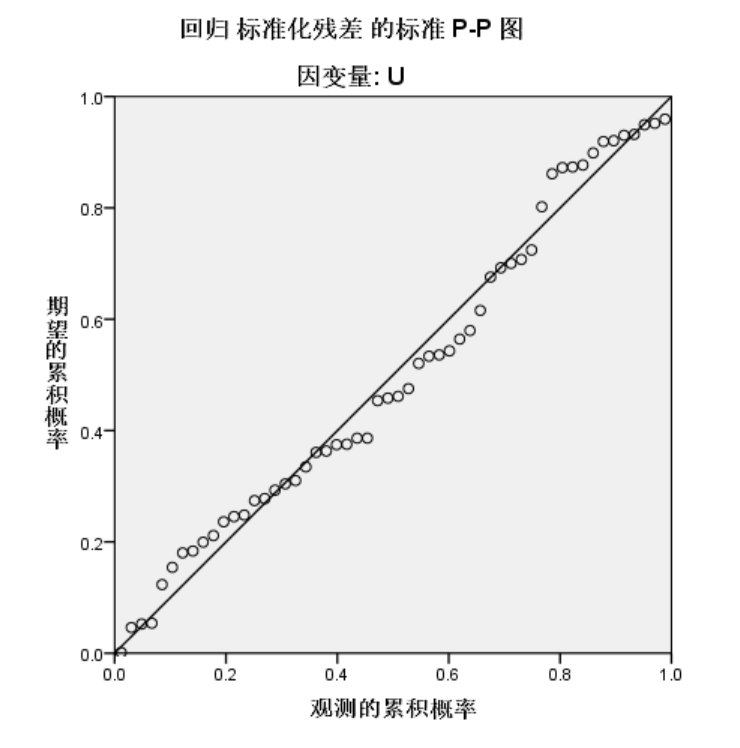
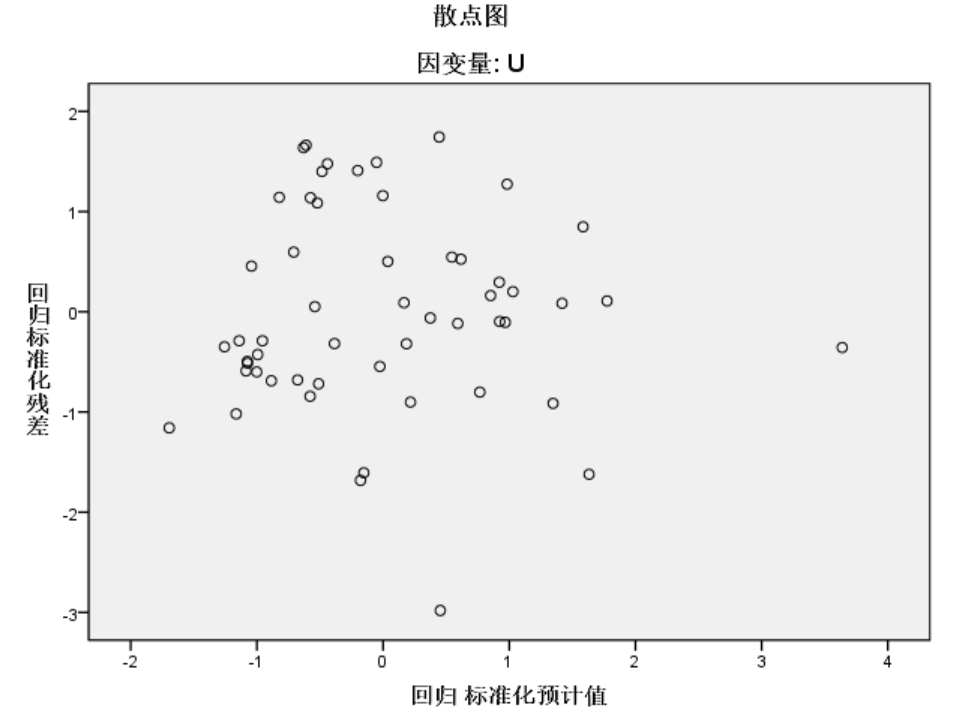
残差基本落在[-2,2]范围内，最后得到的经验方程是：
$$U=0.01X+0.54$$