[数据结构与算法]堆排序实现

之前笔者在遇到一些需要用到堆的算法题，如 n 个数求最大的 k 个数时经常使用优先队列，Java 类 PriorityQueue 是优先队列实现的一种，本篇我打算通过数组实现堆，并简单说明堆和优先队列的区别

二叉堆（最常见的堆）本质是完全二叉树，二叉树样式也更容易理解，一般通过数组实现，通过数组实现时，具体规则如下图：

完全二叉树：树按照从上到下，从左到右的顺序排列，之间不存在空节点

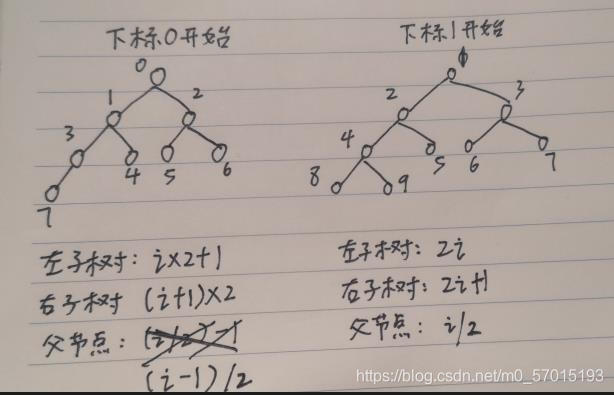
按不同功能，堆可以划分为以下两类：

• 最大堆：节点值大于其左右子树的值，左右子树也是最大堆
• 最小堆：节点值小于其左右子树的值，左右子树也是最小堆

因此一般通过最小堆计算最大的 n 个数，最大堆计算最小的 n 个数，PriorityQueue 默认是最小堆

根据数组构建最小堆 java 源码：

public class Heap {

    /**
     * 构建堆
     *
     * @param num
     * @return
     */
    private void heap(int[] num) {
        if (num == null || num.length == 0) {
            return;
        }
        // 从最后一个父节点开始反向遍历
        int n = num.length, start = getParentIndex(n - 1);
        for (; start >= 0; --start) {
            dealNode(num, start, n);
        }
    }

    /**
     * 处理对应父节点
     *
     * @param num
     * @param index
     */
    private void dealNode(int[] num, int index, int length) {
        int left = getLeftIndex(index), right = getRightIndex(index);
        // 左节点不存在直接跳出
        if (left >= length) {
            return;
        }
        int v = num[index], lv = num[left], rv;
        // 右节点不存在只处理左节点，此时左节点是末尾节点
        if (right >= length) {
            num[index] = Math.min(v, lv);
            num[left] = Math.max(v, lv);
            return;
        }
        rv = num[right];
        // 如果左节点值最小
        if (lv <= v && lv <= rv) {
            num[index] = lv;
            num[left] = v;
            // 递归判断左子树
            dealNode(num, left, length);
        }
        // 如果右节点值最小
        if (rv <= v && rv <= lv) {
            num[index] = rv;
            num[right] = v;
            // 递归判断右子树
            dealNode(num, right, length);
        }
    }

    /**
     * 返回左子树下标
     *
     * @param i
     * @return
     */
    private int getLeftIndex(int i) {
        return i * 2 + 1;
    }

    /**
     * 返回右子树下标
     *
     * @param i
     * @return
     */
    private int getRightIndex(int i) {
        return (i + 1) * 2;
    }

    /**
     * 返回父节点下标
     *
     * @param i
     * @return
     */
    private int getParentIndex(int i) {
        return (i - 1) / 2;
    }

}

除了构建堆，有时还借助堆的特性实现排序的效果：最小堆首元素最小，最大堆首元素最大，可以通过依次交换首、尾节点并重新构建堆的方式实现排序。每轮可以找出最 大/小 值，也就是说：最小堆可以实现从大到小排列，最大堆可以实现从小到大排列

最小堆实现从大到小排列源码如下：

/**
 * 最小堆从大到小排列数组
 *
 * @param heap：已经满足堆结构的数组
 */
private void exchange(int[] heap) {
    if (heap == null || heap.length == 0) {
        return;
    }
    for (int i = heap.length - 1; i > 0; --i) {
    	// 每次将最后一个元素换到首部
        int temp = heap[0];
        heap[0] = heap[i];
        heap[i] = temp;
        // 通过 i 充当界限，达到断开连接的效果
        dealNode(heap, 0, i);
    }
}

其实对于计算前 n 个数，最 大/小 的 k 个数只需创建长度为 k 的数组，初始并构建堆，对于新来的元素每次先和堆顶元素比较，满足条件替换并重新构建堆即可，最后剩下的即是所求

最后简单聊聊优先队列和堆的区别：

1. 优先队列本质仍是一种特殊的队列，而堆不是
2. 优先队列有很多种实现，PriorityQueue 只是其中一种，碰巧和二叉堆功能类似，堆实际也有很多种，上面介绍的只是最常见的二叉堆
3. 从算法角度来说，特殊队列大小是会扩容的，需要人工控制长度，而堆理论上固定大小，无须人工额外控制