[数据结构与算法] xor相关（持续更新）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> xor相关（持续更新） -> 正文阅读

[数据结构与算法]xor相关（持续更新）

T1 The XOR Largest Pair

01trie模板题

#include<bits/stdc++.h>
#define LL long long
#define N 101010
using namespace std;

int son[N*30][2],idx[N*30],tot,n,a[N];

void insert( int pos,int x )
{
	int p = 0;
	for(int i=31;i>=0;i--)
	{
		int &temp = son[ p ][ (x>>i) & 1 ];
		if( !temp )
		{
			temp = ++tot;
		}
		p = temp;
	}
	idx[p] = pos;
}

int search( int x )
{
	int p = 0;
	for(int i=31;i>=0;i--)
	{
		int s = (x>>i)&1;
		if( son[p][!s] ) p = son[p][!s];
		else p = son[p][s];
	}
	return idx[p];
}

void solve()
{
	int ans = 0;
	cin>>n;
	a[0] = 0;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		ans = max( ans , a[ search( a[i] ) ] ^ a[i] );
		insert( i,a[i] );
	}
	cout<<ans;
}

int main()
{
	solve();
	return 0;
}

T2 奶牛异或

对于区间的问题，我们希望转化成和两个端点相关的问题去做——区间[l,r]的异或和等于前r个数的异或和和前l-1个数的异或和异或，所以，我们只需要在前缀异或和数组里面任选两个数让他们异或和最大即可，于是就和前一个题一样了。

#include<bits/stdc++.h>
#define LL long long
#define N 101010
using namespace std;

int son[N*20][2],idx[N*20],tot,n,a[N],y;

void insert( int pos,int x )
{
	int p = 0;
	for(int i=21;i>=0;i--)
	{
		int &temp = son[ p ][ (x>>i) & 1 ];
		if( !temp )
		{
			temp = ++tot;
		}
		p = temp;
	}
	idx[p] = pos;
}

int search( int x )
{
	int p = 0;
	for(int i=21;i>=0;i--)
	{
		int s = (x>>i)&1;
		if( son[p][!s] ) p = son[p][!s];
		else p = son[p][s];
	}
	return idx[p];
}

void solve()
{
	cin>>n;
	a[0] = 0;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&y);
		a[i] = a[i-1] ^ y;
//		ans = max( ans , a[ search( a[i] ) ] ^ a[i] );
//		insert( i,a[i] );
	}
	insert(0,0);
	int temp,l=1,id,r=n,ans=-1;
	for(int i=1;i<=n;i++)
	{
		int j = search( a[i] );
		temp = a[i] ^ a[j];
		j++;
		if( temp > ans || (temp==ans && i<r) )
		{
			ans = temp;
			l = j;
			r = i;
		}
		insert( i,a[i] );
	}
	cout<<ans<<" "<<l<<" "<<r;
}

int main()
{
	solve();
	return 0;
}

T3 Vitya and Strange Lesson

题意：就是给定一串序列，然后有一系列全局异或操作，问你每次操作后，没有出现过的最小的非负整数

idea：
这题我感觉挺有意思的

方法1）反着来，我们可以把，不在数组中的所有数字加入树，然后通过查找与0异或最小的数即为答案。

#include<bits/stdc++.h>
#define LL long long
#define N 300010
#define rep(i,x,y) for( auto i=(x);i<=(y);++i )
#define dep(i,x,y) for( auto i=(x);i>=(y);--i )
using namespace std;
bool pd[N*2];
int tire[N*20][2],idx[N*20],tot = 0,ans,a[N],q[N],n,m,b[N],cnt[N*20];

void insert(int pos,int x)
{
	int p = 0;
	for(int i=21;i>=0;i--)
	{
		int &t = tire[p][ (x>>i) &1 ];
		if( !t )
		{
			tot++;
			t = tot;
		}
		p = t;
	}
	idx[p] = pos;
}

int search(int x)
{
	int sum = 0;
	int p = 0;
	int temp,s;
	for(int i=21;i>=0;i--)
	{
//		cout<<i<<" "<<sum<<endl;
		temp = (x>>i) & 1;
		s = tire[p][ temp ];
		if( s )
		{
			p = s;
		}
		else
		{
			p = tire[p][!temp];
			sum |= (1<<i);
		}
	}
	return sum;
}

void solve()
{
	cin>>n>>m;
	memset(tire,0,sizeof(tire));
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		pd[ a[i] ] = true;
//		insert(i,a[i]);
	}
	for(int i=0;i<=N*2;i++)
	{
		if( !pd[i] ) insert( i,i );
	}
	b[0] = 0;
	for(int i=1;i<=m;i++)
	{
		int x;
		scanf("%d",&x);
		b[i] = b[i-1] ^ x;
		printf("%d\n",search(b[i]));
	}
	
}

int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
 }

法2）正着来，考虑如何在 01tire树上找到最小没有出现过的数
我们可以在每次插入一个数的时候，对形成的路径上的每一个点权值 +1
如果这个点对应的是二进制下第 i 位(最低位为 0)，且这个点的权值为 1<<i，那么这颗子树一定是个满二叉树，即这个点的子树中并不存在没有出现过的非负整数，所以这个点不能出现在我们的查询路径中
所以如果 0 的那棵子树满了就可以直接去到 1 的子树中，这样能保证至少有一棵树不是满二叉树所以，第一个不在字典树上的数就是我们要求的的答案

然后的问题就是如何做到全局异或一个值呢？

首先来想一想，如果没有全局异或的操作，我们应该如何查询？按照上面的方法，我们的查询应该是从零开始找，然后在从高位向低位跳的时候，如果 0 的那棵子树满了，就跳向 1 的子树，直到找到第一个不在树上的数
那如果有异或呢，每次操作我们可以认为是原数异或上之前所有操作的异或和（这样trie树不会发生变化）。于是我们每次要做的是在01trie中找到一个和当前的x（也就是本次和之前操作的异或和）异或值最小且不存在于树上的树——如果x的当前位是1，我们这一层往下也倾向于往1走，此时判断1的子树是否满了，如果满了就不能走了只能往0走，如果没满就往1走使得当前位异或的结果为0；当前位为0也类似的思考，一直找下去就行了。

#include<bits/stdc++.h>
#define LL long long
#define N 300010
#define rep(i,x,y) for( auto i=(x);i<=(y);++i )
#define dep(i,x,y) for( auto i=(x);i>=(y);--i )
using namespace std;
bool pd[N];
int tire[N*20][2],idx[N*20],tot = 0,ans,a[N],q[N],n,m,b[N],cnt[N*20];

void insert(int pos,int x)
{
	int p = 0;
	for(int i=21;i>=0;i--)
	{
		if( !tire[p][ (x>>i) & 1 ] ) tire[p][ (x>>i) & 1 ] = ++tot;
		cnt[ tire[p][ (x>>i) & 1 ] ]++;
		p = tire[p][ (x>>i) & 1 ];
	}
	idx[p] = pos;
}

int search(int x)
{
	int sum = 0;
	int p = 0;
	int temp,s;
	for(int i=21;i>=0;i--)
	{
		temp = (x>>i) & 1;
		if( cnt[ tire[p][temp] ] == (1<<i) )
		{
			p = tire[p][temp^1];
			sum |= (1<<i);
		}
		else
		{
			p = tire[p][temp];
		}
		if( !p ) return sum;
	}
	return sum;
}

void solve()
{
	cin>>n>>m;
	memset(tire,0,sizeof(tire));
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		if( !pd[ a[i] ] ) insert(i,a[i]);
		pd[ a[i] ] = true;
	}
	b[0] = 0;
	for(int i=1;i<=m;i++)
	{
		int x;
		scanf("%d",&x);
		b[i] = b[i-1] ^ x;
		printf("%d\n",search(b[i]));
	}
	
}

int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
 }

T4 Perfect Security
题意：
在这里插入图片描述
分析：

在这里插入图片描述

#include<bits/stdc++.h>
#define LL long long
#define N 301000
using namespace std;

int son[N*20][2],idx[N*20],tot = 0,n,a[N],cnt[N*20],b[N],ans[N];

inline void insert(int pos,int x)
{
	int p = 0;
	for(int i=30;i>=0;i--)
	{
		if( !son[p][  (x>>i) & 1 ] ) son[p][ (x>>i) & 1 ] = ++tot;
		cnt[ son[p][ (x>>i) & 1 ] ]++;
		p = son[p][ (x>>i) & 1 ];
	}
	idx[p] = pos;
}

inline int search(int x)
{
	int temp,s,p = 0;
	for(int i=30;i>=0;i--)
	{ 
		s = (x>>i) & 1;
		if( cnt[ son[p][s] ] > 0 )
		{
			cnt[ son[p][s] ]--;
			p = son[p][s];
		}
		else cnt[ son[p][s^1] ]-- , p = son[p][s^1];
	}
	return idx[ p ];
}

void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&b[i]);
		insert( i,b[i] );
	}
	for(int i=1;i<=n;i++)
	{
		printf("%d ",b[ search(a[i]) ] ^ a[i]);
	}
}
int main()
{
	solve();
	return 0;
}

T4 最大异或和

可持久化Trie模板题

我们发现实际上就是考虑一个区间的数和 xx 异或后的最大异或和。

这样我们建一棵可持久化Trie ,每个节点存它的数字个数，查询的时候从高位到低位贪心走路就好。

另外注意一个坑点，就是如果查询区间左端点是1的话， x 异或上 00 可能是最大的，要把这种情况考虑进去。

//（yxc的板子）
#include<bits/stdc++.h>
#define LL long long
#define INF 0x3f3f3f3f
using namespace std;

const int N = 600010;
int n,m,s[N],tr[N*25][3],max_id[N*25],root[N],idx = 0;

void insert(int i, int k, int p, int q)
{
	if (k < 0)
	{
		max_id[q] = i;
		return;
	}
	int v = s[i] >> k & 1;
	if (p) tr[q][v ^ 1] = tr[p][v ^ 1];
	tr[q][v] = ++ idx;
	insert(i, k - 1, tr[p][v], tr[q][v]);
	max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]);
}

int query(int root, int C, int L)
{
	int p = root;
	for (int i = 23; i >= 0; i -- )
	{
		int v = C >> i & 1;
		if (max_id[tr[p][v ^ 1]] >= L) p = tr[p][v ^ 1];
		else p = tr[p][v];
	}
	return C ^ s[ max_id[p] ];
}

void solve()
{
	scanf("%d%d",&n,&m);
	s[0] = 0;
	max_id[0] = -1;
	root[0] = ++idx;
	insert( 0,23,0,root[0] );
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		s[i] = s[i-1] ^ x;
		root[i] = ++idx;
		insert( i,23,root[i-1],root[i] );
	}
	
	int l,r,x;
	char op[2];
	while( m-- )
	{
		
		scanf("%s",op);
		if( *op=='A' )
		{
			scanf("%d",&x);
			n++;
			s[n] = s[n-1] ^ x;
			root[n] = ++idx;
			insert( n,23,root[n-1],root[n] );
		}
		else
		{
			scanf("%d%d%d",&l,&r,&x);
			printf("%d\n",query( root[r-1] , s[n]^x ,l-1));
		}
	}
}

int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
}

T5 Xor-MST

XOR-MST模板
模板栏有所收录

#include<bits/stdc++.h>
#define LL long long
#define N 200010
#define INF 0x3f3f3f3f
using namespace std;

LL ans;
int tr[N*30][2],tot = 0,sum,a[N],n,idx[N*30];
//tr是trie树，a数组记录个点权值，idx记录trie树上叶子结点的所对应的权值

void clear(int p)
{
	tr[p][0] = tr[p][1] = 0;//反复使用trie注意清零
	return ;
}

void insert(int x)//插入建trie树
{
	int p = 0;
	for(int i=30;i>=0;i--)
	{
		int v =(x>>i) & 1;
		if( !tr[p][v] ) 
		{
			tr[p][v] = ++tot;
			p = tr[p][v];
			clear(p);//注意清空
		}
		else p = tr[p][v];
	}
	idx[p] = x;
}

int find(int x)//查询与X异或之后得到的异或值最小是多少，即最小的边权
{
	int sum = 0,p = 0;
	for(int i=30;i>=0;i--)
	{
		int v = (x>>i) & 1;
		if( !tr[p][v] ) 
		{
			v ^= 1;
		}
		p = tr[p][v];
	}
	return idx[p];
}


void dfs(int l,int r,int dep)//跑dfs的时候分治
{
	if( dep < 0 ) return ; //（二进制）从最高位开始，一直划分到个位
	int mid = l;
	for(int i=l;i<=r;i++)//找那个当前二进制位是1的那个分界点
	{
		if( (a[i]>>dep) & 1 == 1 )
		{
			mid = i;
			break;
		}
	}
	if( mid<=r ) dfs(mid,r,dep-1);// (1<<id)==1的划分为一个集合
	if( l<mid ) dfs(l,mid-1,dep-1);// (1<<id)==0的划分为一个集合
	if( l < mid && mid <= r )//如果这个点可以成为LCA，就合并它的左右两子树
	{
		tot = 0;
		clear(tot);
		for(int i=l;i<=mid-1;i++) insert( a[i] );
		int minn = INF;
		for(int i=mid;i<=r;i++)
		{
			minn = min( minn , a[i] ^ find( a[i] ) );
		}
		ans += minn;//加上可以成为MST中一条边的边权
	}
}

void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	sort(a+1,a+n+1);//排序以保证贪心的正确性,下一步根据大小划分集合
	dfs(1,n,30);
	printf("%lld\n",ans);
}

int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
}

T6 CF703D Mishka and Interesting sum

PS：本题可以看做下题的前缀知识or思想

题意：查询区间中出现偶数次的数的异或和

idea:首先，区间出现偶数次的数的异或 = 区间出现过的数的异或 ^ 区间出现奇数次的数的异或。
其次，任何一个数对自身进行偶数次异或都等于0，奇数次异或等于这个数自身。
所以区间出现奇数次的数的异或直接打一个前缀。
对于区间出现过的数的异或，假设一开始直接维护一个[1,n]的大区间，那么在具体位置对于每个数是否出现过我们是不得而知的，也就是没有办法实现状态之间的转移，所以我们动态的维护一个（1，x）的区间，对于每个在x位置出现的数，我们要让它
只对x及以后的区间产生作用，即让每一个出现的数尽可能的往后排。

#include<bits/stdc++.h>
#define LL long long
#define N 1001000 
using namespace std;
int n,m;
map<int,int> last;
int a[N],c[N],sum[N],ans[N];
int lowbit(int x)
{
	return x & (-x);
}
void add(int p,int val)
{
	while( p<=n )
	{
		c[p] ^= val;
		p += lowbit(p);
	}
}

int query(int p)
{
	int sum = 0;
	while( p )
	{
		sum ^= c[p];
		p -= lowbit(p);
	}
	return sum;
}

struct node
{
	int l,r,id;
	bool operator < (const node &u)const
	{
		return r<u.r;
	}
}q[N];

void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		sum[i] = a[i] ^ sum[i-1];
	}
	cin>>m;
	for(int i=1;i<=m;i++)
	{
		scanf("%d %d",&q[i].l,&q[i].r);
		q[i].id = i;
	}
	sort( q+1,q+m+1 );
	for(int p=1,i=1;i<=m;i++)
	{
		while( p<=q[i].r )
		{
			add( p,a[p] );
			if( last[ a[p] ]!=0 ) add( last[ a[p] ] , a[p] );
			last[ a[p] ] = p;
			p++; 
		}
		ans[ q[i].id ] = sum[ q[i].r ] ^ sum[ q[i].l-1 ] ^ query( q[i].r ) ^ query( q[i].l-1 );
	}
	for(int i=1;i<=m;i++)
	{
		printf("%d\n",ans[i]);
	}
}

int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
}

T7 HDU多校 I love counting

本蒟蒻写的题解
trie + 树状数组 + 分拆询问到trie上

#include<bits/stdc++.h>
#define LL long long
#define N 100010
#define PB push_back
using namespace std;
int n,c[N],m,bit[N],ans[N];
struct node
{
	int l,r,ne,id;//ne表示当前节点的后继节点的位置
	bool operator < (const node & u)const
	{
		if( ne!=u.ne ) return ne > u.ne;//只统计后继节点不在这个区间的点
		else if( id!=u.id ) return id > u.id;//询问在前
		else return l < u.l;
	}
};

vector<node> ve[N*20];

int lowbit(int x)
{
	return x & (-x);
}

void bit_add(int p,int v)
{
	while( p<=n )
	{
		bit[p] += v;
		p += lowbit(p);
	}
}

int bit_query(int p)
{
	int sum = 0;
	while( p )
	{
		sum += bit[p];
		p -= lowbit(p);
	}
	return sum;
}


int tr[N*20][2],tot = 0,last[N],ne[N];

void insert(int x,int id)
{
	int p = 0;
	for(int i=20;i>=0;i--)
	{
		int v = (x>>i) & 1;
		if( !tr[p][v] ) tr[p][v] = ++tot;
		p = tr[p][v];
		ve[ p ].PB( node{ id, 0, ne[id], 0 } );
	}
	
}

void query(int l,int r,int a,int b,int id)
{
	int  p = 0,v1,v2;
	for(int i=20;i>=0;i--)
	{
		v1 = (a>>i) & 1;
		v2 = (b>>i) & 1;
		if( v2==1 )
		{
			if( tr[p][v1] ) ve[ tr[p][v1] ].PB( node{ l,r,r,id } );
			p = tr[p][v1^1];
			if( !p ) break;
		}
		else
		{
			p = tr[p][v1];
			if( !p ) break;
		}
	}
	ve[p].PB( node{ l, r, r, id } );在结尾处添加询问
}

void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&c[i]);
	}
	cin>>m;
	for(int i=n;i>=1;i--)
	{
		if( !last[ c[i] ] ) ne[i] = n+1;
		else ne[i] = last[ c[i] ];
		last[c[i]] = i;
	}
	for(int i=1;i<=n;i++)
	{
		insert( c[i],i );
	}
	int l,r,a,b;
	for(int i=1;i<=m;i++)
	{
		scanf("%d %d %d %d",&l,&r,&a,&b);
		query( l, r, a, b, i );
	}
	for(int i=1;i<=tot;i++)
	{
		sort( ve[i].begin(), ve[i].end() );
		int sz = ve[i].size();
		for(int j=0;j<sz;j++)
		{
			if( ve[i][j].id == 0 )
			{
				bit_add( ve[i][j].l , 1 );//做插入
			}
			else
			{
				ans[ ve[i][j].id ] += bit_query( ve[i][j].r ) - bit_query( ve[i][j].l - 1 );
			}
		}
		for(int j=0;j<sz;j++)
		{
			if( ve[i][j].id == 0 )
			{
				bit_add( ve[i][j].l , -1 );
			}
		}
	}
	for(int i=1;i<=m;i++)
	{
		printf("%d\n",ans[i]);
	}
	return ;
}

int main()
{
	//freopen("in.txt","r",stdin);
	solve();
	return 0;
}

T8 CF Mikasa

题意：给你n和m，一个序列是这样的
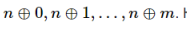
在这里插入图片描述
求这个序列的mex。

idea：首先有 $n$ $\bigoplus$ $m$ $=$ $k$ 等价于 $n$ $\bigoplus$ $k$ $=$ $m$ ,所欲其实我们是要找到一个最小的 $k$ ，满足 $n$ $\bigoplus$ $k$ $> =$ $m + 1$ （不用trie，就两个数）

ACcode：

#include<bits/stdc++.h>
#define LL long long
using namespace std;
 
LL t,n,m,tot = 0;
 
LL find(LL x,LL y)
{
	int tag,ans = 0;
	for(int i=30;i>=0;i--)
	{
		int v1 = (x>>i) & 1;
		int v2 = (y>>i) & 1;
		if( v2==1 && v1==0 )
		{
			ans |= 1 << i;
		}
		else if( v1==1 && v2==0 )
		{
			return ans;
		}
	}
	return ans;
}
 
void solve()
{
	scanf("%lld %lld",&n,&m);
	printf("%lld\n",find(n,m+1));	
}
 
int main()
{
//	freopen("in.txt","r",stdin);
	cin>>t;
	while( t-- ) solve();
	return 0;
}