Leetcode 1104.二叉树寻路

题目链接: leetcode 1104.二叉树寻路

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点逐行依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

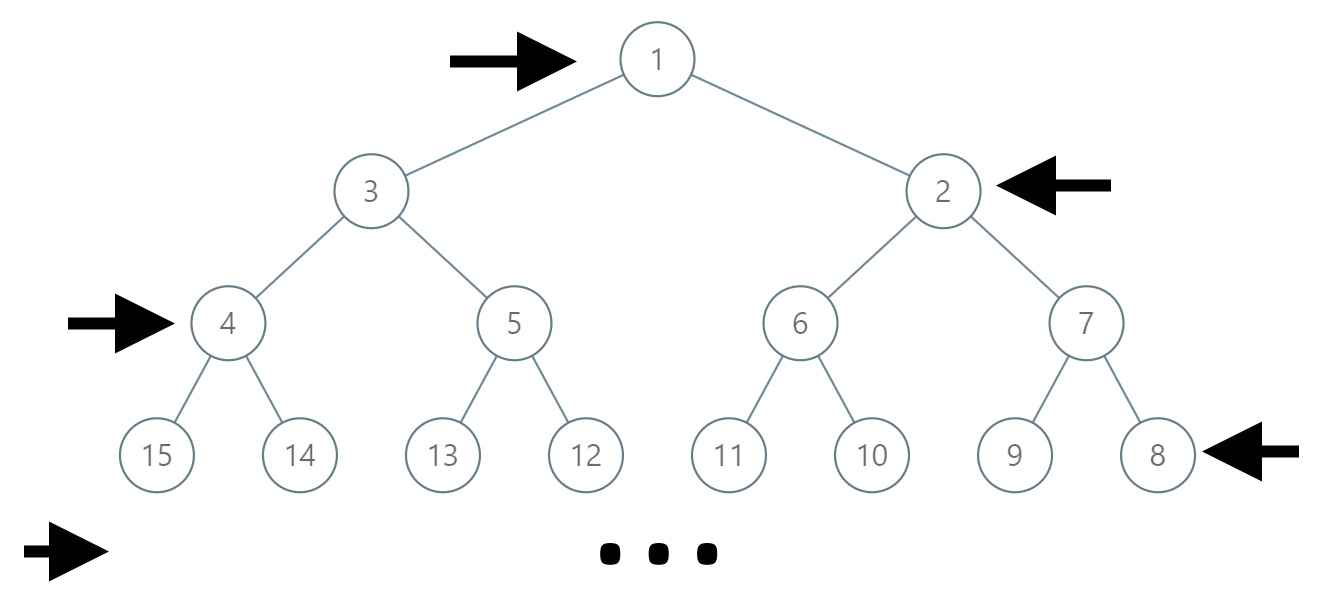
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

样例

示例1:
输入：label = 14
输出：[1,3,4,14]
    
示例2:
输入：label = 26
输出：[1,2,6,10,26]

提示:

$\le label \le 10^6$ ?

算法1

思路分析

根据题意可以知道这是一棵完全二叉树, 如果其标记的顺序不是按照题目的之字形进行标记, 而是按照正常的从上到下,从左到右的顺序依次标记, 那么我们对于其标号x的关系有, 其左孩子为 2 * x，其右孩子为 2 * x + 1; 其父节点为 x / 2 (x > 1); 此时对于根节点到label的路径为1–>…–> label / 4 --> label / 2 --> label。那么按照题目的意思,此时偶数层的标号会被逆序, 奇数层保持不变。那么此时的label的情况就有两种.

(1) 此时label节点位于奇数层 (第 x 层, 根节点为第一层)

如果此时label位于奇数层, 那么此时其父节点即为偶数层, 其原本的父节点应该为 label / 2, 但由于偶数层相比于原本其顺序是相反的, 故此时的标号为 $2^{x - 2} + 2^{x - 1} - 1 - label / 2$ , 这个式子是如何推到的呢? 首先对于label的上一层即第 x - 1层, 其原本的最左边的节点标记为 $2^{x - 2}$ , 其最右边标记为 $2^{x - 1}$ - 1, 而我们知道从左到右每个节点的标记都是递增1, 现在反转了标记顺序, 故可以得到原本的标记值 + 新的标记值 = $2^{x - 2} + 2^{x - 1}$ - 1 所以知道原本的标记值应该为 label/2, 那么此时新的标记值为 $2^{x - 2} + 2^{x - 1} - 1 - label / 2$ ?.

(2) 此时label节点位于偶数层 (第 x 层)

同理如果此时的label位于偶数层, 那么此时的父节点即为奇数层, 即父节点的标记与原本完全二叉树的相同,而自身label是反转后的新值, 故我们要求出此时label的旧值, 然后用旧值 / 2 即得到父节点的标记值, 得到label旧值的方法同上, 此时旧标记值 + 新标记值(即label) = $2^{x - 1} + 2^x - 1$ , 故其原本的标记值为：

$2^{x - 1} + 2^x - 1$ - label , 故其父节点的值为 ( $2^{x - 1} + 2^x - 1$ ? - label) / 2;

基于上面的分析, 那么我们最开始的时判断我们的label是偶数层还是奇数层, 首先这棵二叉树原本是属于完全二叉树, 故对于标记值为label, 且其位于的层数为x, 那么则存在 label < $2^x$ ?, 故这里我们可以用二分的方法快速求出label位于第几层。

C++ 代码

class Solution 
{
public:
    vector<int> pathInZigZagTree(int label) 
    {
        vector<int> res; 
        int l = 1, r = 20; 
        while(r > l)                     // 二分求出label位于第几层 
        { 
            int mid = l + r >> 1; 
            if(label <= pow(2, mid) - 1) r = mid; 
            else l = mid + 1; 
        }

        int n = l, num = label;        // n 表示当前层数, num 表示此时要加入的标记值 
        while(n != 1)
        {
            res.push_back(num); 
            if(n % 2) num = (pow(2, n - 2) + pow(2, n - 1) - 1  - num /  2); 
            else num = (pow(2, n - 1) + pow(2, n) - 1 - num) / 2; 
            --n;
        }

        res.push_back(1);                  // 最后加入根节点
        reverse(res.begin(), res.end());   // 由于从下往上遍历, 故最后要翻转
        return res; 
    }
};