[数据结构与算法]决策树和熵

决策树和熵

一:熵

1.熵:用于衡量不确定性

公式:
$$\begin{gathered} H(x)=?\sum (pi)?log(pi) \\ 例如:x取值,x_1=0.5,x_2=0.5 \\ H(x)=?0.5log0.5?0.5log0.5=0.69 \end{gathered}$$

2.联合概率熵

$$H(x,y)=?\sum P(x_i,y_i)logP(x_i,y_i)$$

3.条件概率熵

$$\begin{gathered} H(X|Y)=\sum _{j=1}^{n}P(y_i)H(x|y_i) \\ 表示:在y成立条件下的x的分布 \end{gathered}$$

4.概率熵的关系

二:信息增益

理解为减少的信息熵

怎么计算减少了多少信息增益(减少的信息熵)?

例子:10个样本里,7个为1,3个为0

样本熵,可以理解为贝叶斯的先验概率:

? H(X) = -0.7log0.7-0.3log0.3 = 0.078 + 0.138 = 0.265 (这里使用10作为log的底)

假如有特征A/B/C

A的取值 A1(3个1,1个0) , A2(2个1,2个0) , A3(2个1)

B的取值 B1(3个1,2个0) , B2(4个1,1个0)

计算A的熵,可以理解为后验概率:

? H(X|A) = 0.4H(A1)+0.4H(A2)+0.2H(A3) = 0.4(-3/4log(3/4)-1/4log(1/4))+0.4(-1/2log(1/2)*2)+0.2(-1log(1))

? =0.037+0.06+0.12+0 = 0.217

计算B的熵:

? H(X|B) = 0.5H(B1)+0.5(B2) = 0.5(-3/5log(3/5)-2/5log(2/5))+0.5(-4/5log(4/5)-1/4log(1/4))

? =0.146+0.109 = 0.255

计算信息增益:

I(X|A)=H(X)-H(X|A) = 0.265-0.217 = 0.048

I(X|B)=H(X)-H(X|B) = 0.265-0.255 = 0.01

结论:说明A特征的信息增益=0.048 , 就是说特征A减少了样本不确定性的程度为0.048;

B特征的信息增益=0.01 , 就是说特征B减少了样本不确定性的程度为0.01

三:如何构建决策树

根据信息增益最大值取一个特征作为根节点(如果有一致的信息增益值就随机)

问题:随机节点就会出现多种决策树,从而引申出随机森林

例子:通过上面信息熵的案例举例

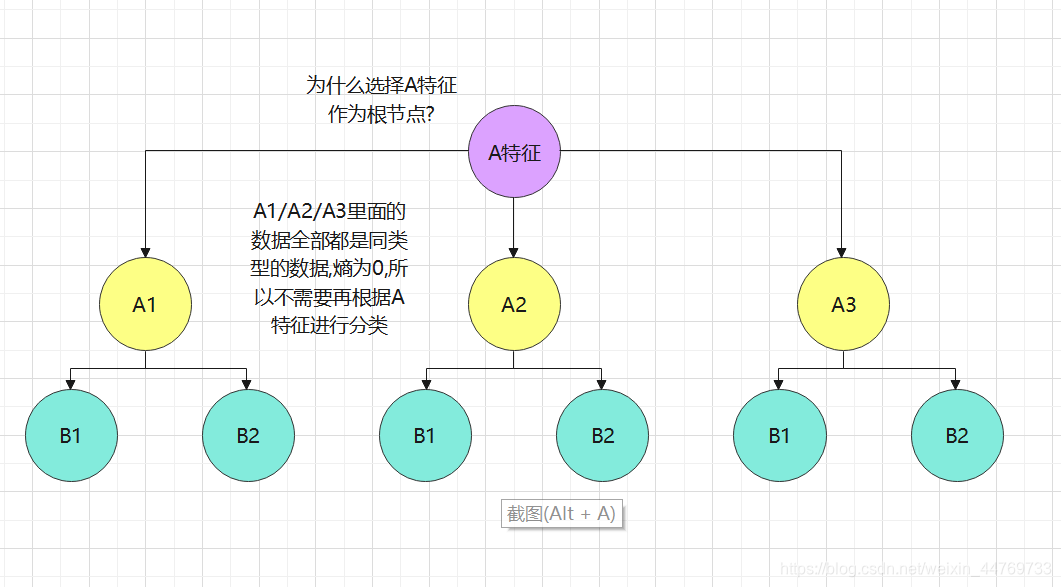
问题1:决策树什么时候停止,即不再分发叶子节点呢?

1.把所有特征全部分裂完成

2.把所有产生信息增益的特征拆分完成,没有信息增益或者信息增益很小(设置的信息增益阈值)的特征不再分裂

3.叶子节点数据量=1

4.达到最大深度 / 最小叶子数 / 最小样本分裂数

问题2:过拟合和欠拟合

如果强行分裂到最小节点,则可能会发生过拟合

如果信息增益的阈值太高,则可能发生欠拟合

缺点:

1.ID3算法不能解决连续变量的问题:可以通过分区间再取中间值或者均值进行划分特征,但是碰到数据量特别大的连续变量怎么办?
2.不能解决回归问题

3.多叉树在存储和计算上没有二叉树快

4.log对数计算耗时

5.容易过拟合