题意
- Double Strings | 2021牛客暑期多校训练营5
有两个字符串
A
,
B
A,B
A,B
拿出
A
A
A 的一个子序列
a
a
a ,
B
B
B 的一个子序列
b
b
b
满足
∣
a
∣
=
∣
b
∣
|a|=|b|
∣a∣=∣b∣ 且字典序
a
<
b
a<b
a<b
问方案数 -
1
≤
∣
A
∣
,
∣
B
∣
≤
5000
1\le |A|,|B|\le 5000
1≤∣A∣,∣B∣≤5000
记号
- 为了后文方便描述,我们做一些记号
∣
A
∣
|A|
∣A∣ 表示字符串
A
A
A 的长度
∣
a
∣
|a|
∣a∣ 表示字符串
A
A
A 的一个子序列
a
a
a 的长度
A
[
1
,
i
]
A[1,i]
A[1,i] 表示字符串
A
A
A 下标从
1
1
1 取到
i
i
i 的一个子串 (
b
a
s
e
1
base 1
base1)
a
<
b
a<b
a<b 表示子序列
a
a
a 的字典序小于子序列
b
b
b
时间复杂度中的
N
N
N 表示两个字符串的长度的较大值
S
i
S_i
Si? 表示字符串
S
S
S 的第
i
i
i 位
思路
- 首先注意到范围,基本只能
O
(
N
2
)
O(N^2)
O(N2) 去做
因为两个子序列字典序满足
a
<
b
a<b
a<b,所以一定存在
i
,
j
i,j
i,j ,满足
a
i
<
b
j
a_i<b_j
ai?<bj?
那么这个子序列的前部分和后部分怎么样呢?
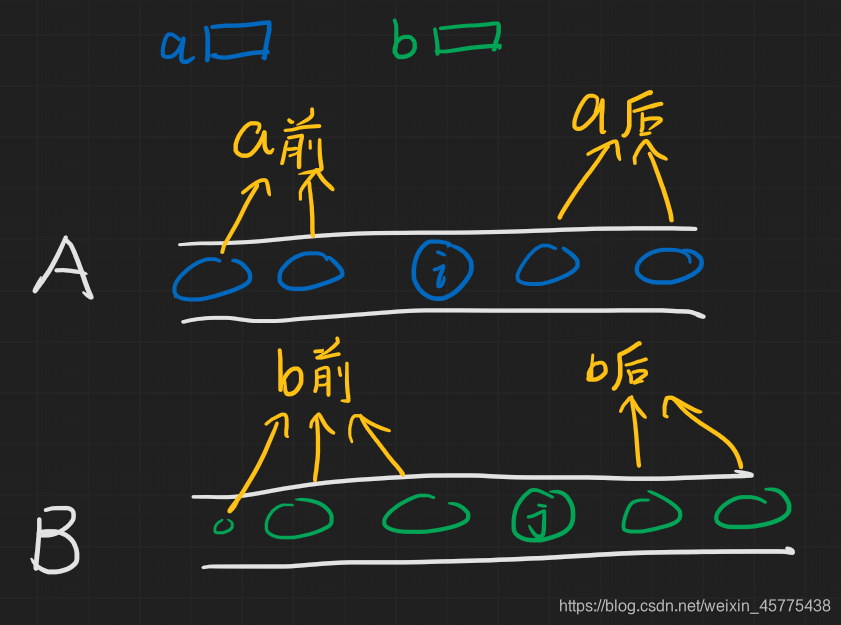 - 容易想到,
a
前
=
b
前
a前=b前
a前=b前 且
∣
a
后
∣
=
∣
b
后
∣
|a后|=|b后|
∣a后∣=∣b后∣
于是我们就把原问题分成了两个子问题:
(1)
A
[
1
,
i
]
A[1,i]
A[1,i] 与
B
[
1
,
j
]
B[1,j]
B[1,j] 之间,有多少个相同的子序列
(2)
a
后
a后
a后 与
b
后
b后
b后 有多少种取法,满足它们的长度相同
第二个子问题
- 容易想到是和
∣
A
∣
?
i
|A|-i
∣A∣?i 与
∣
B
∣
?
j
|B|-j
∣B∣?j 的大小有关系,与后面的字符是无关的
我们化简一下问题,令第一个串
S
S
S 第二个串
T
T
T ,我们从第一个串取出子序列
s
s
s ,第二个串取出子序列
t
t
t ,满足
∣
s
∣
=
∣
t
∣
|s|=|t|
∣s∣=∣t∣ 的方案数,后面简称为方案数
对于任意的
∣
S
∣
|S|
∣S∣ 与
∣
T
∣
|T|
∣T∣ 我们都需要得到,状态数是
O
(
N
2
)
O(N^2)
O(N2) 的
从数学的角度讲,答案为:
∑
i
=
1
min
?
(
∣
S
∣
,
∣
T
∣
)
C
∣
S
∣
i
C
∣
T
∣
i
\sum_{i=1}^{\min(|S|,|T|)} C_{|S|}^i C_{|T|}^i
i=1∑min(∣S∣,∣T∣)?C∣S∣i?C∣T∣i?
但是貌似直接算一次时间复杂度为
O
(
N
)
O(N)
O(N),我们总复杂度为
O
(
N
3
)
O(N^3)
O(N3) ,明显承受不起
【但是赛后看别人,这个式子可以直接化简的,不过假设我们不知道结论,怎么去做】
所以我们从
d
p
dp
dp 的角度出发 - 设
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示第一个串考虑了前
i
i
i 个位置,第二个串考虑了前
j
j
j 个位置,方案数是多少
想到,我们是怎么枚举状态的?
先是固定
i
i
i 的位置,然后枚举
j
=
1
j=1
j=1 到
j
=
∣
T
∣
j=|T|
j=∣T∣
那么,我们现在要去算
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] ,就假设我们已经得到了之前的
d
p
dp
dp 数组
也就是,第二维从
j
?
1
j-1
j?1 扩到
j
j
j ,我们新增加的贡献是多少?
 - 第一种情况,
T
j
T_j
Tj? 我们不选,那么容易想打方案数就是
d
p
[
i
]
[
j
?
1
]
dp[i][j-1]
dp[i][j?1]
第二种情况,
T
j
T_j
Tj? 我们选,由于两个子序列的长度需要相同,那么我们假设
s
s
s 的最后一位多选一个下标
k
k
k 的位置
此时方案数为多少呢?容易想到为
d
p
[
k
?
1
]
[
j
?
1
]
dp[k-1][j-1]
dp[k?1][j?1]
由于
k
k
k 的位置有很多种,所以我们需要一个求和。
综上,方案数为:
d
p
[
i
]
[
j
]
=
d
p
[
i
]
[
j
?
1
]
+
∑
k
=
1
i
d
p
[
k
?
1
]
[
j
?
1
]
dp[i][j]=dp[i][j-1]+\sum_{k=1}^{i} dp[k-1][j-1]
dp[i][j]=dp[i][j?1]+k=1∑i?dp[k?1][j?1]
转换一下下标方便计算,变成
d
p
[
i
]
[
j
]
=
d
p
[
i
]
[
j
?
1
]
+
∑
k
=
0
i
?
1
d
p
[
k
]
[
j
?
1
]
dp[i][j]=dp[i][j-1]+\sum_{k=0}^{i-1} dp[k][j-1]
dp[i][j]=dp[i][j?1]+k=0∑i?1?dp[k][j?1] - 由于我们的
i
i
i 也是递增枚举过来的,自然这个时候
∑
k
=
0
i
?
1
d
p
[
k
]
[
j
?
1
]
\sum_{k=0}^{i-1} dp[k][j-1]
∑k=0i?1?dp[k][j?1] 之前是算出来过的
我们使用前缀和便可以
O
(
1
)
O(1)
O(1) 得到
然后由于枚举变量的关系,我们可以使用滚动数组 来让前缀和数组变成空间
O
(
N
)
O(N)
O(N) 的
在代码中命名为
d
p
2
[
i
]
[
j
]
dp2[i][j]
dp2[i][j]
然后再考虑一下边界,就是
d
p
2
[
i
]
[
0
]
=
1
dp2[i][0]=1
dp2[i][0]=1 因为空的子序列也算一种方案
int L1 = strlen(s1+1);
int L2 = strlen(s2+1);
int st = 0;
for(int i = 0;i <= L1;++i){
dp2[i][0] = 1;
pre[0][st^1]++;
for(int j = 1;j <= L2;++j){
dp2[i][j] = (dp2[i][j-1] + pre[j-1][st]) % MOD;
pre[j][st^1] = (pre[j][st^1] + dp2[i][j]) % MOD;
}
for(int j = 0;j <= L2;++j){
pre[j][st] = (pre[j][st] + pre[j][st^1]) % MOD;
pre[j][st^1] = 0;
}
}
第二个子问题的数学做法
- 我们有:
∑
i
=
0
m
C
n
i
C
m
i
=
C
n
+
m
m
\sum_{i=0}^{m}C_n^iC_m^i=C_{n+m}^m
i=0∑m?Cni?Cmi?=Cn+mm?
证明方法:右边等价于:从
n
+
m
n+m
n+m 个不同的球中摸出
m
m
m 个球的方案数
等式左边等价于把
n
+
m
n+m
n+m 个球分成
n
、
m
n、m
n、m 两块
从
n
n
n 个球中摸出
i
i
i 块,从
m
m
m 个球摸出
m
?
i
m-i
m?i 个球
得证
第一个子问题
- 我们之间做过的
L
C
S
LCS
LCS (最长公共子序列) 的问题,是求两个串的
L
C
S
LCS
LCS
这里我们的问题变成了求两个串有多少个非空
C
S
CS
CS
如果
s
i
≠
s
j
s_i\ne s_j
si??=sj? ,根据容斥我们可以得到:
d
p
[
i
]
[
j
]
=
d
p
[
i
]
[
j
?
1
]
+
d
p
[
i
?
1
]
[
j
]
?
d
p
[
i
?
1
]
[
j
?
1
]
dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]
dp[i][j]=dp[i][j?1]+dp[i?1][j]?dp[i?1][j?1]
如果
s
i
=
s
j
s_i=s_j
si?=sj?,也根据容斥,我们有
d
p
[
i
]
[
j
]
=
d
p
[
i
]
[
j
?
1
]
+
d
p
[
i
?
1
]
[
j
]
?
d
p
[
i
?
1
]
[
j
?
1
]
+
d
p
[
i
?
1
]
[
j
?
1
]
+
1
dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1] +\color{red}{dp[i-1][j-1]+1}
dp[i][j]=dp[i][j?1]+dp[i?1][j]?dp[i?1][j?1]+dp[i?1][j?1]+1
+
1
+1
+1 是因为我们让
s
i
、
s
j
s_i、s_j
si?、sj? 单独成为一个子序列
+
d
p
[
i
?
1
]
[
j
?
1
]
+dp[i-1][j-1]
+dp[i?1][j?1] 就是我们让
s
i
、
s
j
s_i、s_j
si?、sj? 拼到之前的所有满足的子序列之中
for(int i = 1;i <= L1;++i){
for(int j = 1;j <= L2;++j){
if( s1[i] == s2[j] )
dp[i][j] = (dp[i-1][j] + dp[i][j-1] + 1) % MOD;
else
dp[i][j] = (dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1]) % MOD;
}
}
- 那么最后的答案怎么去算呢?
只要
A
i
<
B
j
A_i<B_j
Ai?<Bj? ,那么答案就是
(
d
p
[
i
?
1
]
[
j
?
1
]
+
1
)
×
d
p
2
[
∣
A
∣
?
i
]
[
∣
B
∣
?
j
]
(dp[i-1][j-1] + 1) \times dp2[|A|-i][|B|-j]
(dp[i?1][j?1]+1)×dp2[∣A∣?i][∣B∣?j]
加一是因为还有一个空的子序列
然后这里也可以滚动数组滚一下
代码
- 时间复杂度:
O
(
N
2
)
O(N^2)
O(N2)
#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
using namespace std;
typedef long long ll;
void show(){std::cerr << endl;}template<typename T,typename... Args>void show(T x,Args... args){std::cerr << "[ " << x << " ] , ";show(args...);}
const int MAX = 5e3+5;
const int MOD = 1e9+7;
const int INF = 0x3f3f3f3f;
const ll LINF = 0x3f3f3f3f3f3f3f3f;
const double EPS = 1e-5;
char s1[MAX],s2[MAX];
ll dp[2][MAX];
int dp2[MAX][MAX];
ll pre[MAX][2];
int main()
{
scanf("%s%s",s1+1,s2+1);
int L1 = strlen(s1+1);
int L2 = strlen(s2+1);
int st = 0;
for(int i = 0;i <= L1;++i){
dp2[i][0] = 1;
pre[0][st^1]++;
for(int j = 1;j <= L2;++j){
dp2[i][j] = (dp2[i][j-1] + pre[j-1][st]) % MOD;
pre[j][st^1] = (pre[j][st^1] + dp2[i][j]) % MOD;
}
for(int j = 0;j <= L2;++j){
pre[j][st] = (pre[j][st] + pre[j][st^1]) % MOD;
pre[j][st^1] = 0;
}
}
ll ans = 0;
for(int i = 1;i <= L1;++i){
for(int j = 1;j <= L2;++j){
if( s1[i] == s2[j] )
dp[st^1][j] = (dp[st][j] + dp[st^1][j-1] + 1) % MOD;
else
dp[st^1][j] = (dp[st][j] + dp[st^1][j-1] - dp[st][j-1]) % MOD;
if(s1[i] < s2[j]){
ans = (ans + (dp[st][j-1] + 1) * 1LL * dp2[L1 - i][L2 - j] % MOD) % MOD;
}
}
for(int j = 1;j <= L2;++j){
dp[st][j] = dp[st^1][j];
dp[st^1][j] = 0;
}
}
ans = (ans + MOD) % MOD;
printf("%lld",ans);
return 0;
}
|

