二叉树的前序遍历
递归
class Solution {
private:
vector<int>ret;
public:
vector<int> preorderTraversal(TreeNode* root) {
_preorderTraversal(root);
return ret;
}
void _preorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
ret.push_back(root->val);
_preorderTraversal(root->left);
_preorderTraversal(root->right);
}
};
迭代
用一个栈模拟递归顺序,右子树先进栈,左子树后进栈,这样出栈的先是左子树。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if (nullptr == root)
return {};
vector<int>ret;
stack<TreeNode*>stk;
stk.push(root);
while (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
ret.push_back(node->val);
//右子树先进后出
if (node->right)
stk.push(node->right);
//左子树后进先出
if (node->left)
stk.push(node->left);
}
return ret;
}
};
也可以这样写,当遍历到一个节点后,左右节点进栈,优先判断它的右节点,是否为nullptr,再判断它的左节点,然后,自己进栈,最后压入一个nullptr,获取栈顶的节点为nullptr时,可判断栈顶的下面一个节点遍历过。此做法前序遍历的效果不明显,因为前序遍历中,遍历过的节点可以直接丢弃。在中后序遍历效果明显,解决的重复遍历的问题。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
if (nullptr == root)
return {};
vector<int>ret;
stack<TreeNode*>stk;
stk.push(root);
while (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
if (node) {
//右子树先进后出
if (node->right)
stk.push(node->right);
//左子树后进先出
if (node->left)
stk.push(node->left);
stk.push(node);
//栈顶为nullptr,node已经遍历过
stk.push(nullptr);
}
else {
ret.push_back(stk.top()->val);
stk.pop();
}
}
return ret;
}
};
Morris 遍历
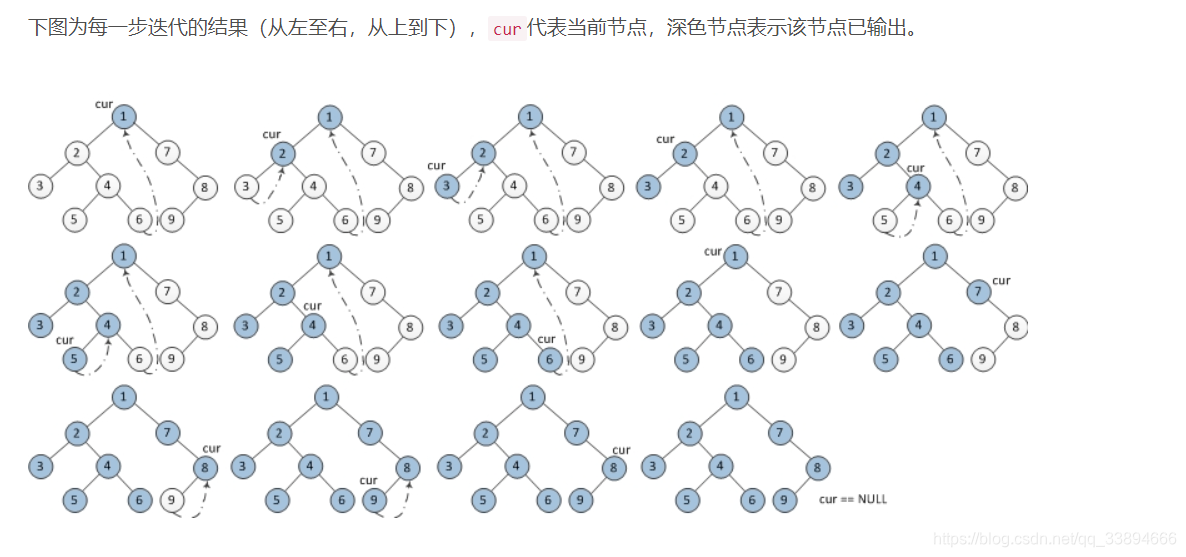
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int>ret;
TreeNode* cur = root;
TreeNode* max_right = nullptr;
while (cur != nullptr) {
if (cur->left) {
max_right = cur->left;
while (max_right->right != nullptr && max_right->right != cur)
max_right = max_right->right;
if (max_right->right == nullptr) {
max_right->right = cur;
ret.push_back(cur->val);
cur = cur->left;
}
else if (max_right->right == cur) {
max_right->right = nullptr;
cur = cur->right;
}
}
else {
ret.push_back(cur->val);
cur = cur->right;
}
}
return ret;
}
};
二叉树的中序遍历
递归
class Solution {
private:
vector<int>ret;
public:
vector<int> inorderTraversal(TreeNode* root) {
_inorderTraversal(root);
return ret;
}
void _inorderTraversal(TreeNode* root) {
if (nullptr == root)
return;
_inorderTraversal(root->left);
ret.push_back(root->val);
_inorderTraversal(root->right);
}
};
迭代
当遍历到一个节点后,左右节点进栈,优先判断它的右节点,是否为nullptr,然后,自己进栈,再压入一个nullptr,最后,判断它的左节点。如果一个节点的左右都不为nullptr的话,栈中的内容应该是:
栈底[node->right, node, nullptr, node->left]栈顶
获取栈顶的节点为nullptr时,可判断栈顶的下面一个节点遍历过。此做法前序遍历的效果不明显,因为前序遍历中,遍历过的节点可以直接丢弃。在中后序遍历效果明显,解决的重复遍历的问题。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
if (nullptr == root)
return {};
vector<int>ret;
stack<TreeNode*> stk;
stk.push(root);
while (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
if (node != nullptr) {
if (node->right)
stk.push(node->right);
stk.push(node);
stk.push(nullptr);
if (node->left)
stk.push(node->left);
}
else {
ret.push_back(stk.top()->val);
stk.pop();
}
}
return ret;
}
};
Morris 遍历

class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int>ret;
TreeNode* cur = root;
TreeNode* max_right = nullptr;
while (cur != nullptr) {
if (cur->left) {
max_right = cur->left;
while (max_right->right != nullptr && max_right->right != cur) {
max_right = max_right->right;
}
if (max_right->right == nullptr) {
max_right->right = cur;
cur = cur->left;
}
else if (max_right->right == cur) {
ret.push_back(cur->val);
max_right->right = nullptr;
cur = cur->right;
}
}
else {
ret.push_back(cur->val);
cur = cur->right;
}
}
return ret;
}
};
二叉树的后序遍历
递归
class Solution {
private:
vector<int>ret;
void _postorderTraversal(TreeNode* root) {
if (nullptr == root)
return;
_postorderTraversal(root->left);
_postorderTraversal(root->right);
ret.push_back(root->val);
}
public:
vector<int> postorderTraversal(TreeNode* root) {
_postorderTraversal(root);
return ret;
}
};
迭代
当遍历到一个节点后,自己进栈,然后压入一个nullptr,左右节点进栈,优先判断它的右节点是否为nullptr,再判断它的左节点。
如果一个节点的左右都不为nullptr的话,栈中的内容应该是:
栈底[node ,nullptr,node->right,node->left]栈顶
获取栈顶的节点为nullptr时,可判断栈顶的下面一个节点遍历过。此做法前序遍历的效果不明显,因为前序遍历中,遍历过的节点可以直接丢弃。在中后序遍历效果明显,解决的重复遍历的问题。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if (nullptr == root)
return {};
vector<int>ret;
stack<TreeNode*>stk;
stk.push(root);
while (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
if (nullptr != node) {
stk.push(node);
stk.push(nullptr);
if (node->right)
stk.push(node->right);
if (node->left)
stk.push(node->left);
}
else {
ret.push_back(stk.top()->val);
stk.pop();
}
}
return ret;
}
};
Morris遍历
与常规的不太相同,将前序遍历顺序"root root->left root->right"替换成"root root->right root->left",完成后,反转数组即为后序遍历的顺序。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int>ret;
TreeNode* cur = root;
TreeNode* max_left = nullptr;
while (cur != nullptr) {
if (cur->right) {
max_left = cur->right;
while (max_left->left != nullptr && max_left->left != cur)
max_left = max_left->left;
if (max_left->left == nullptr) {
ret.push_back(cur->val);
max_left->left = cur;
cur = cur->right;
}
else if (max_left->left == cur) {
max_left->left = nullptr;
cur = cur->left;
}
}
else {
ret.push_back(cur->val);
cur = cur->left;
}
}
reverse(ret.begin(), ret.end());
return ret;
}
};