[数据结构与算法]九大经典排序算法（王道考研排序算法整理）

6. 排序

算法稳定性：若待排序表有两个元素 $R_i$ 和 $R_j$，其对应的关键字相同即 $ke{y}_i=ke{y}_j$，且排序前 $R_i$ 在 $R_j$ 前面。

• 若排序后 $R_i$? 仍然在 $R_j$?? 前面，则是稳定的。
• 反之亦然? 👊

6.1 直接插入排序

初始 $L[1]$ 可以视为已经排好的子序列，然后依次将 $L[2]?l[n]$ 插入已经排好的序列，共执行 $n?1$ 次操作。每次操作的具体步骤为从后往前依次和子序列元素比较，如果小于该元素往后移位，最后将自己插入适当的位置。

// 直接插入排序
void DirectInsertSort(ElementType A[], int n)
{
    int i, j;
    for (i = 2; i <= n; i++)
    {
        // 看是否比序列大，如果大就不用移动位置，反之要进入循环移动位置
        if (A[i] < A[i - 1])
        {
            // 放置哨兵
            A[0] = A[i];
            for (j = i - 1; A[j] > A[0]; j--)
            {
                // 向后移位
                A[j + 1] = A[j];
            }
            // 将哨兵里元素放到属于他的位置
            A[j + 1] = A[0];
        }
    }
}

空间复杂度：$O(1)$

时间复杂度：

• 最好情况：初始有序，每次插入元素就比较一次而不用移动元素，时间复杂度 $O(n)$
• 最坏情况：初始逆序，时间复杂度 $O(n^2)$
• 平均时间复杂度 $O(n^2)$?

6.2 折半插入排序

查询元素位置用二分查找实现，但与二分查找不同，二分查找是查到元素的位置，但这里其实是通过左右比较，找到一个适当的位置，所以最后会以 $high=low?1$? 结束，所以 $high$? 指向元素就是应该插入元素的前一个元素。然后再统一向后移动元素。

// 折半插入排序
void BinaryInsertSort(ElementType A[], int n)
{
    int i, j, mid, low, high;
    for (int i = 2; i <= n; i++)
    {
        A[0] = A[i];
        low = 1, high = i - 1;
        // 二分查找定位置
        while (low <= high)
        {
            mid = (low + high) / 2;
            if (A[mid] > A[0])
            {
                high = mid - 1;
            }
            else
            {
                low = mid + 1;
            }
        }
        // 最后会以high=low-1结束，所以high指向元素就是应该插入元素的前一个元素
        // 那么high+1表示的就是应该插入元素的位置
        for (j = i - 1; j >= high + 1; j--)
        {
            A[j + 1] = A[j];
        }
        A[high + 1] = A[0];
    }
}

空间复杂度：$O(1)$

时间复杂度：

• 仅减少了比较元素的次数，未改变移动次数，因此平均时间复杂度还是 $O(n^2)$?

6.3 希尔排序

将相隔某一增量的元素组成子表，对每个子表直接插入排序。这个某一增量的取值一般为 $d_1=n/2，d_{i+1}=d_i/2$，到最后一个增量为1为止。相当于在元素基本有序时，对全体进行一次直接插入排序。

// 希尔排序
void ShellSort(ElementType A[], int n)
{
    // 记录步长
    for (int dk = n / 2; dk >= 1; dk = dk / 2)
    {
        for (int i = dk + 1; i <= n; i++)
        {
            if (A[i] < A[i - dk])
            {
                A[0] = A[i];
                int j;
                for (j = i - dk; A[0] < A[j] && j > 0; j -= dk)
                {
                    A[j + dk] = A[j];
                }
                A[j + dk] = A[0];
            }
        }
    }
}

空间复杂度：$O(1)$

时间复杂度：

• 分析十分复杂，记住最优情况下约为 $O(n^{1.3})$?，最坏情况下 $O(n^2)$??

6.4 冒泡排序

从后往前两两比较相邻元素的值，若为逆序则交换。这是第一趟冒泡。结果是最小的元素到了第一个位置。下一趟冒泡，已经确定的最小元素不用参与，最多重复 $n?1$? 趟冒泡就能把所有元素排好序。

// 冒泡排序
void BubbleSort(ElementType A[], int n)
{
    for (int i = 0; i < n - 1; ++i)
    {
        // 判断本趟冒泡是否发生交换的标志
        bool flag = false;
        for (int j = n - 1; j > i; j--)
        {
            if (A[j - 1] > A[j])
            {
                swap(A[j - 1], A[j]);
                flag = true;
            }
        }
        if (!flag)
        {
            break;
        }
    }
}

空间复杂度：$O(1)$

时间复杂度：

• 最好情况：初始有序，只进行一次冒泡，时间复杂度 $O(n)$
• 最坏情况：初始逆序，需要 $n?1$ 次排序，时间复杂度 $O(n^2)$
• 平均时间复杂度 $O(n^2)$?

6.5 ??快速排序

任取一元素 $pivot$?? 作为枢轴，一趟排序分成2部分，$pivot$? 左边所有元素小于它，$pivot$?? 右边所有元素大于?它。然后分别递归的对两个子表重复上述过程。直到每部分只有一个元素。

// 快速排序
void QuickSort(ElementType A[], int low, int high)
{
    // 当子序列只剩一个元素时，pivot-1=low，这时high=low，函数结束
    if (low < high)
    {
        // 划分得到枢轴点位置
        int pivotpos = Partition(A, low, high);
        QuickSort(A, low, pivotpos - 1);
        QuickSort(A, pivotpos + 1, high);
    }
}

// 快速排序划分操作
int Partition(ElementType A[], int low, int high)
{
    // 选取第一个元素为枢轴点
    ElementType pivot = A[low];
    while (low < high)
    {
        // 循环找从右向左小于pivot的元素
        while (A[high] >= pivot && high > low)
        {
            high--;
        }
        // 找到该元素将该元素移到左端
        A[low] = A[high];
        while (A[low] <= pivot && high > low)
        {
            low++;
        }
        // 将比枢轴大的元素移到右端
        A[high] = A[low];
    }
    // 此时low=high，存放枢轴元素的值
    A[low] = pivot;
    return low;
}

空间复杂度：$O(lo{g}_{2}n)$???

时间复杂度：$O(lo{g}_{2}n)$

6.6 简单选择排序

就每次都选择序列中最小的元素，重复 $n?1$ 趟。

// 简单选择排序
void SelectSort(ElementType A[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        int j, min = i;
        for (j = i + 1; j < n; j++)
        {
            if (A[j] < A[min])
            {
                min = j;
            }
        }
        if (min != i)
        {
            swap(A[i], A[min]);
        }
    }
}

空间复杂度：$O(1)$???

时间复杂度：$O(n^2)$

6.7 ??堆排序

根据堆的特性，最大堆堆顶元素就是最大值，输出堆顶元素后，将堆底元素放到堆顶，此时堆的性质被破坏，需要重新调整。

? 待解决问题？

• 1?? 如何将无序序列构造成初始堆？
• 2?? 输出堆顶元素后，如何调整堆？

对于 $n$ 个结点的完全二叉树，最后一个结点的父节点是 $n/2$，所以从 $n/2$ 为根结点的子树开始向前筛选，使子树成为堆。筛选方法：看结点是否大于左右子结点值，如小于，与左右子结点中较大者交换。交换后可能会破环下一级堆，于是继续调整。

// 堆排序
void HeapSort(ElementType A[], int len)
{
    BuildMaxHeap(A, len);
    for (int i = len; i > 1; i--)
    {
        // 将根结点与末尾结点交换位置，那么最大元素就被移到数组最后面
        swap(A[i], A[1]);
        // 同时调整堆的时候只对前面i-1元素进行，这样影响不到后面的已排好元素
        HeadAdjust(A, 1, i - 1);
    }
}

// 建堆
void BuildMaxHeap(ElementType A[], int len)
{
    for (int i = len / 2; i > 0; i--)
    {
        HeadAdjust(A, i, len);
    }
}

// 调整堆
void HeadAdjust(ElementType A[], int k, int len)
{
    // A[0]暂时存放子树的根结点
    A[0] = A[k];
    for (int i = 2 * k; i <= len; i *= 2)
    {
        // i如果等于len则没有右子树，也就没有比较左右子树的必要了
        if (i < len && A[i] < A[i + 1])
        {
            i++;
        }
        if (A[i] <= A[0])
        {
            break;
        }
        else
        {
            // 将A[i]复制到父节点
            A[k] = A[i];
            // 修改k，用以定位子树根结点应该放置的位置
            k = i;
        }
    }
    A[k] = A[0];
}

空间复杂度：$O(1)$???

时间复杂度：$O(nlo{g}_{2}n)$

6.8 ??归并排序

待排序表有 $n$?? 个记录，就看成 n 个有序的子表，每个子表长度为1，然后两两归并，得到 $n/2$ 个长度为2或者1个有序表，继续两两归并，直到合并成一个长度为 $n$ 的有序表为止。

// 归并排序
void MergeSort(ElementType A[], int low, int high)
{
    // 划分子序列，分到每个子序列长度为1
    if (low < high)
    {
        int mid = (low + high) / 2;
        MergeSort(A, low, mid);
        MergeSort(A, mid + 1, high);
        Merge(A, low, mid, high);
    }
}

// 归并操作
void Merge(ElementType A[], int low, int mid, int high)
{
    int i = low;
    int j = mid + 1;
    int k;
    // 把子序列所有元素复制到B数组
    for (int k = low; k <= high; k++)
    {
        B[k] = A[k];
    }

    for (k = low; i <= mid && j <= high; k++)
    {
        // 两个子序列相互比较，当一个序列的元素被安置完后
        // 另外一个序列的剩余元素肯定是大于且有序的，直接顺序插入
        if (B[i] < B[j])
        {
            A[k] = B[i++];
        }
        else
        {
            A[k] = B[j++];
        }
    }
    // 如果第一个表没有检测完，复制
    while (i <= mid)
    {
        A[k++] = B[i++];
    }
    // 同理
    while (j <= high)
    {
        A[k++] = B[j++];
    }
    // 注：只有一个while会执行
}

空间复杂度：$O(n)$?????

时间复杂度：$O(nlo{g}_{2}n)$

6.9 基数排序

以关键字是1000一下的整数为例，基数 $r=10$，每个关键字由3个子关键字组成：$k^1{K}^2{K}^3$，分别代表百位，十位和个位，从次位开始（个位）依次进行操作。

次位优先基数排序过程：

• 分配

  ? 创建 $r=10$ 个空桶，按照每个元素的当前子关键字数值放置到不同的桶中

• 收集

  ? 把每个桶的结点首尾相连，形成一个新的线性表

#include <iostream>
using namespace std;

struct node
{
    int data;
    node *next;
};

// 获得一个数的各个位上的数字
int GetDigit(int X, int D)
{
    // 默认次位D=1, 主位D<=MaxDigit
    int d, i;
    for (i = 1; i <= D; i++)
    {
        d = X % 10;
        X /= 10;
    }
    return d;
}

int main()
{
    // 基数
    int radix = 10;
    // 建立桶
    node *bucket[radix];
    // 初始化待排序数组
    int A[10] = {278, 109, 63, 930, 589, 184, 505, 269, 8, 83};
    node *list = NULL;
    node *p;
    for (int i = 0; i < 10; i++)
    {
        node *tmp = new node;
        tmp->data = A[i];
        tmp->next = NULL;
        if (list == NULL)
        {
            list = tmp;
            p = list;
        }
        else
        {
            p->next = tmp;
            p = p->next;
        }
    }
    // 开始排序，对每一位进行处理
    for (int i = 1; i <= 3; i++)
    {
        // 清空桶
        for (int i = 0; i < radix; i++)
        {
            bucket[i] = NULL;
        }
        p = list;
        node *tmp;
        // 分配
        while (p)
        {
            tmp = p;
            p = p->next;
            int k = GetDigit(tmp->data, i);
            if (bucket[k] == NULL)
            {
                bucket[k] = tmp;
            }
            else
            {
                node *q = bucket[k];
                while (q->next)
                {
                    q = q->next;
                }
                q->next = tmp;
            }
            tmp->next = NULL;
        }
        // 收集
        list = NULL;
        for (int j = 0; j < radix; j++)
        {
            if (bucket[j] == NULL)
            {
                continue;
            }
            // 链表首指针定位
            if (bucket[j] && list == NULL)
            {
                list = bucket[j];
                p = list;
                continue;
            }
            // 此时p任指向上一个存在的桶
            while (p->next)
            {
                p = p->next;
            }
            // 如现在的桶存在，让上一个桶的最后一个结点指过来
            p->next = bucket[j];
        }
        // 打印
        cout << i << " trip: ";
        p = list;
        while (p)
        {
            cout << p->data << " ";
            p = p->next;
        }
        cout << endl;
    }
    system("pause");
    return 0;
}

$r$ 为桶个数，d为子关键字个数（趟数），$n$ 为元素个数

空间复杂度：$O(r)$???????

时间复杂度：$O(d(n+r))$

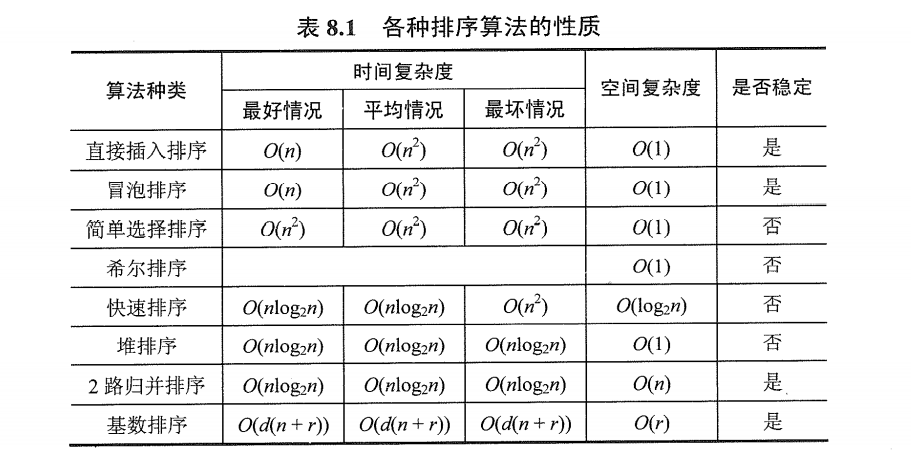
6.10 ??总结