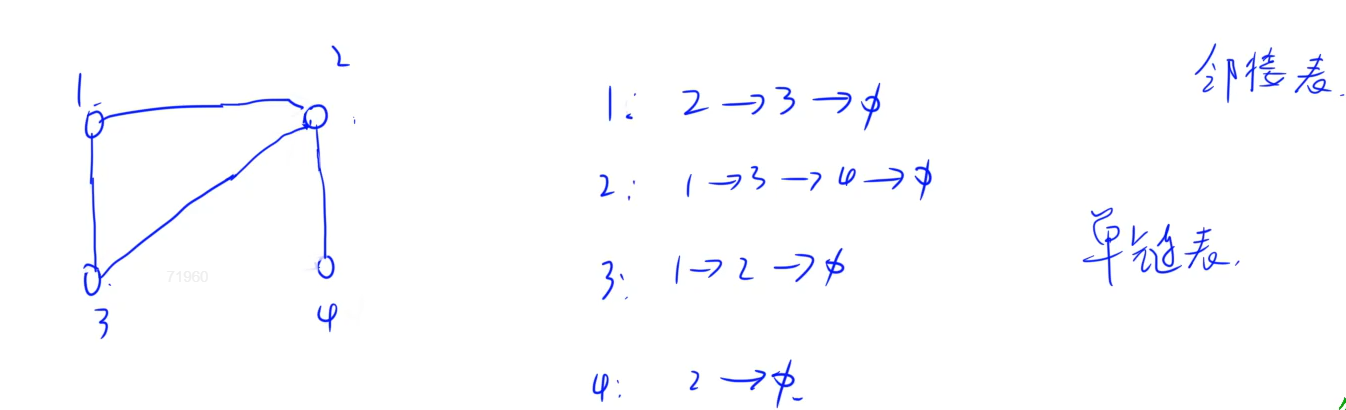目录
1.图的基本概念
(1) 有向图、无向图
(2) 度数(出度、入度)有向图(度数= 出度+ 入度)
(3) 简单图:不存在顶点到其自身的边,且同一条边不重复出现
(4) 路径、环、简单路径(路径不包括重复的点和边)
(5) 无向完全图:任意两个顶点之间都存在边,有n个顶点的无向完全图有 n × (n - 1) / 2条边
C n 2 C_n^2 Cn2?
(6) 有向完全图:任意两个顶点之间都存在方向护卫相反的两条弧,有n个顶点的无向完全图有 n × (n - 1) 条弧
A n 2 A_n^2 An2?
(7) 稀疏图&稠密图:有很少条边或弧的图称为稀疏图,反之称为稠密图,相对的概念。
2.图的存储及基本操作
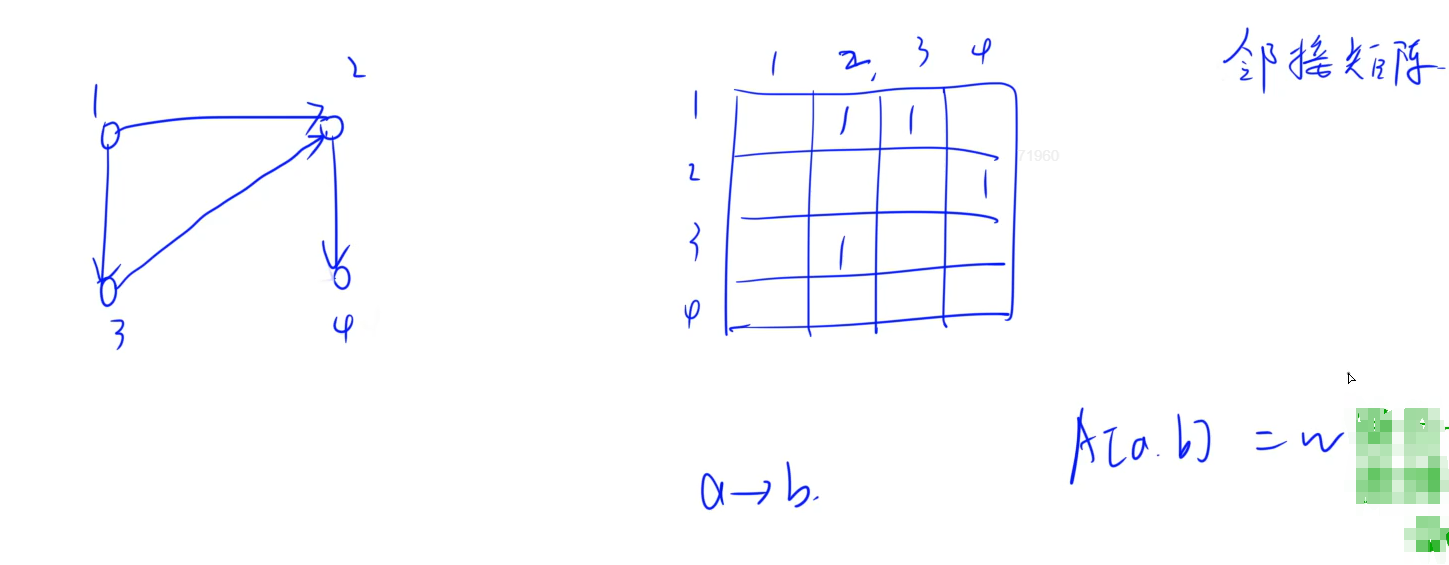
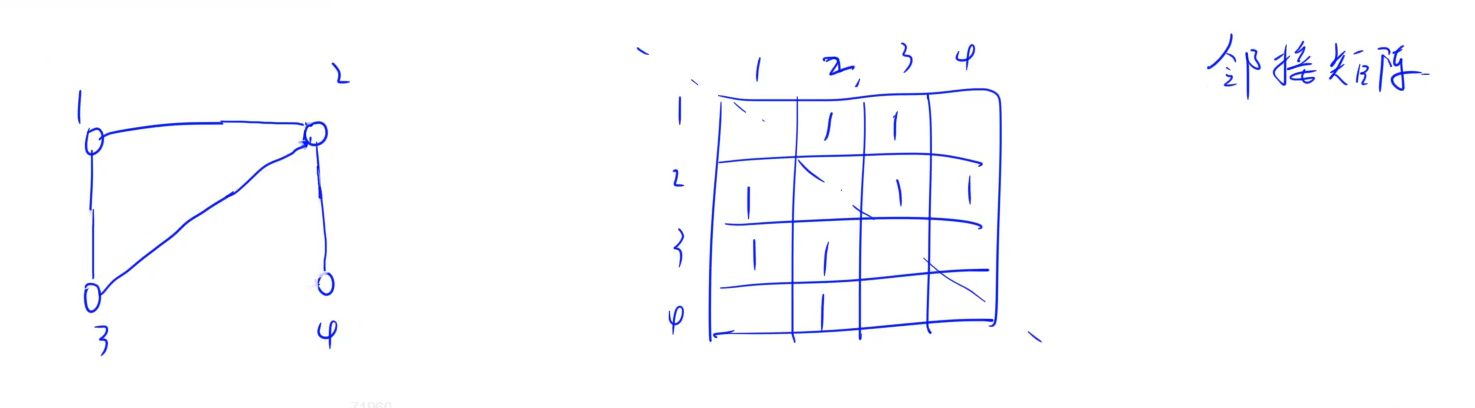
(1) 邻接矩阵:适用于稠密图,可存有向图、无向图。常用。空间复杂度: O ( n 2 ) O(n^2) O(n2) 无法存重边
O ( n 2 ) O(n^2) O(n2)
无向图每条边看成2条有向边
(2) 邻接表:适用于稀疏图,可存有向图、无向图。常用。空间复杂度:O(n + m) O(m) 可存重边
可存储重边 使用最多
上机用的最多 vector set stack queue?
当有重边:
(3) 邻接多重表,适用于稀疏图,可存无向图。不常用。空间复杂度:O(n + m) 可重存边
领接表 不方便找反向边
领接表优化为邻接多重表
上机不会用,因为oj中会用数组模拟链表,存储连续,相邻的就是反向边。
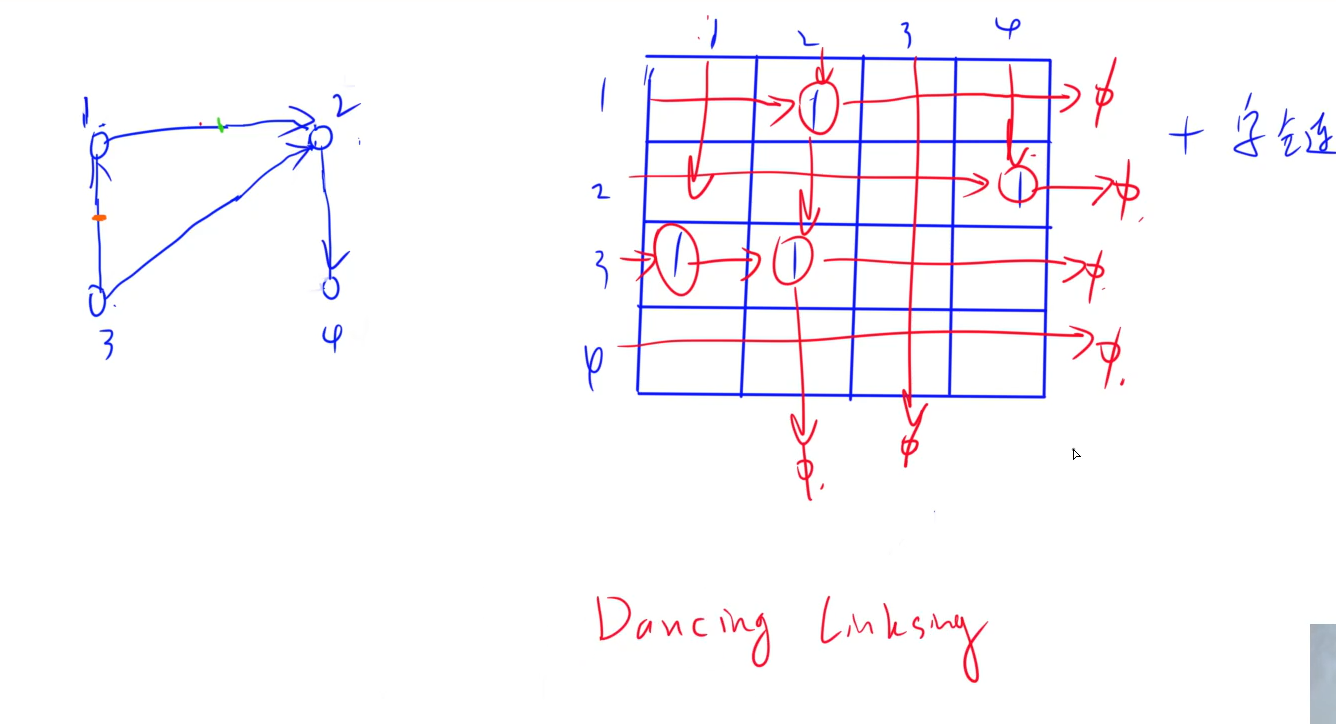
(4) 十字链表,适用于稀疏图,可存有向图、无向图。不常用。空间复杂度:O(n + m) 不能存重边
对邻接矩阵优化
(5) 三元组表,适用于稀疏图,可存有向图,无向图。常用于Bellman-Ford算法、Kruskal算法。空间复杂度:O(m)
m条边 O ( m ) O(m) O(m)

3.图的遍历
(1) 深度优先搜索。邻接表存储的时间复杂度: O ( n + m ) O(n + m) O(n+m)。邻接矩阵存储的时间复杂度: O ( n 2 ) O(n^2) O(n2)
DFS : 能走就必须走, 判重
深搜:能走就走,可能撞了南墙才会回头吧、
(2) 广度优先搜索。邻接表存储的时间复杂度: O ( n + m ) O(n + m) O(n+m)。邻接矩阵存储的时间复杂度: O ( n 2 ) O(n^2) O(n2)
bfs 宽搜 求最短路径
4.拓扑排序
拓扑排序:存在拓扑排序 == 无环
所有边从前指向后
常用bfs O ( n + m ) O(n+m) O(n+m)
入度为 0 的点、 最后判断是否每个点是否遍历到了
BFS:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+5,M = 1e5+5;
int n,m;
struct Node {
int id;
Node* next;
Node(int _id): id(_id),next(NULL){}
}*head[N];
int d[N] ; // 入度
int q[N] ; //数组模拟队列
void add(int a, int b) // 添加一条边b->a 头插法 3->2->1;
{
auto p = new Node(b);
p->next = head[a];
head[a] = p;
}
// bfs 广搜
bool istopsort(){
int hh = 0, tt = -1 ;
for(int i= 1; i<=n;i++){ // n个点 先找到入度为0的点入队列
if(!d[i]) // 此点入度为0
{
q[++tt]= i ; // 队列入队
}
}
while(hh<=tt){ // 队列不为空
int t = q[hh++]; // 取队头
for(auto p= head[t];p;p=p->next){ //遍历 领接表 队头的链表head[t]
if(-- d[p->id] == 0)
q[++tt] = p->id; // 队头去掉后; 后面相连的点入度-1 ; 为0的入队
}
}
return tt == n - 1 ; //队长是否等于n-1 判断是否所有的点都入队了,就是判断是否所有点遍历到了
}
int main()
{
cin>>n>>m; // n个点 m 条边
while(m--){
int a,b;
cin>>a>>b;
d[b]++ ; // a->b 入度+1
add(a,b); // 插入
}
// for(auto p=head[1];p;p=p->next)
// cout << p->id<<endl;
if(!istopsort()) cout<<-1<<endl; // 不是拓扑排序
else{
// q[N] 打印队列
for(int i=0;i<n;i++)
cout<<q[i]<<' ';
}
return 0;
}
5.考题:2011-8、2012-5、2012-6、2013-7、2013-8、2014-7、2015-5、2016-6、2016-7、2017-3、2017-7、2018-7、2020-6
2011-8

简单路径(路径不包括重复的点和边)
邻接矩阵:适用于稠密图,可存有向图、无向图。常用。空间复杂度:O(n^2) 无法存重边
2012-5
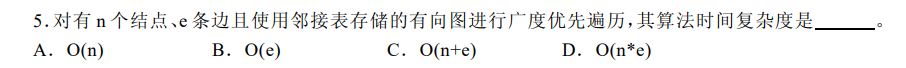
广度
遍历每条边+每个点 O ( n + e ) O(n+e) O(n+e)
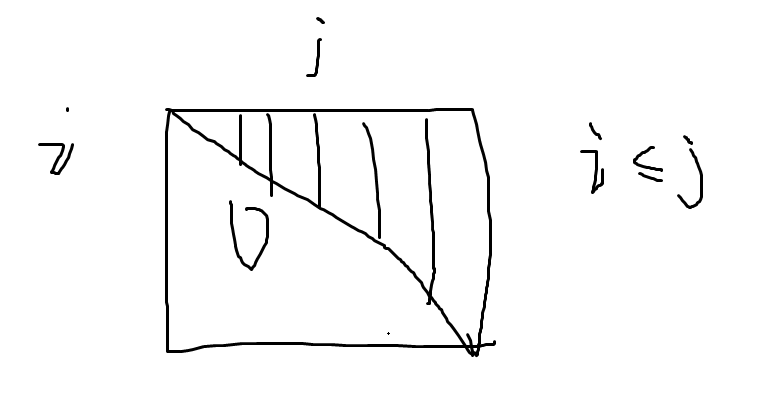
2012-6

i < = j i<= j i<=j
拓扑排序:所有边从前指向后 ,存在,但一定不唯一
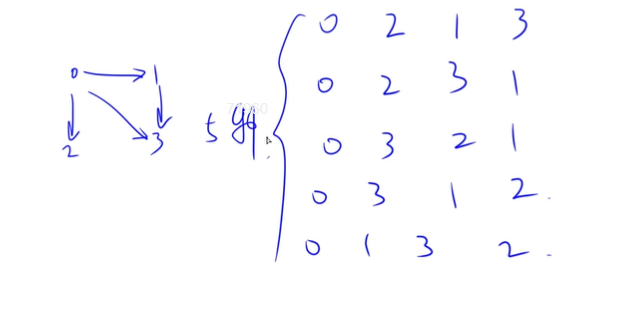
2013-7


2013-8

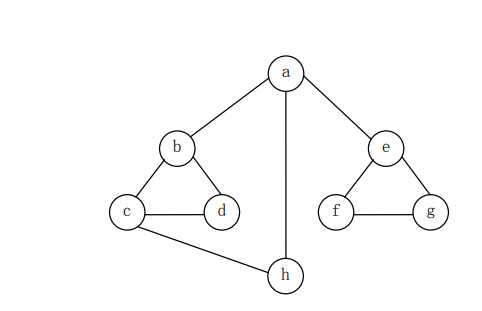
广度即是层次遍历
这种题,我们一定要从 C , D 选项开始看 [dog]
D: a d e D错误
方法:看每个点深度
例如 D: abcdhefg : 01221122 ,不是从小到大即是错的
A:hcabdegf : 01122233
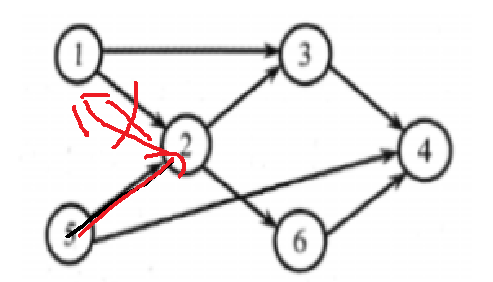
2014-7

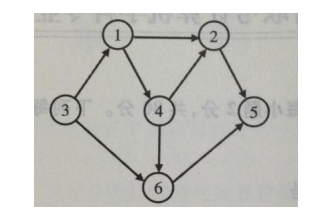
C
2015-5

D
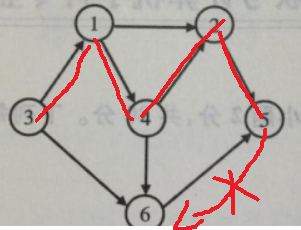
2016-6
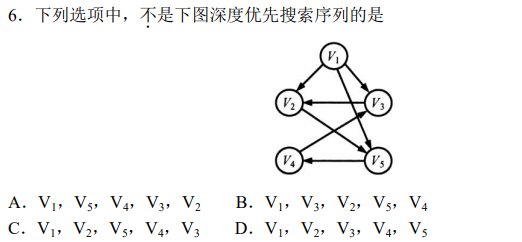
D
1->2->5->4->3
深搜:能走就走,可能撞了南墙才会回头吧、
2016-7

B
2017-3

A
十字链表,适用于稀疏图,可存有向图、无向图。不常用。空间复杂度:O(n + m) 不能存重边, 对邻接矩阵优化
2017-7

16条边,每条边提供2度
$216 - 43 -3*4= 8 $
最大2 ,$ 8/2= 4$
$ 3+4+4= 11$
2018-7
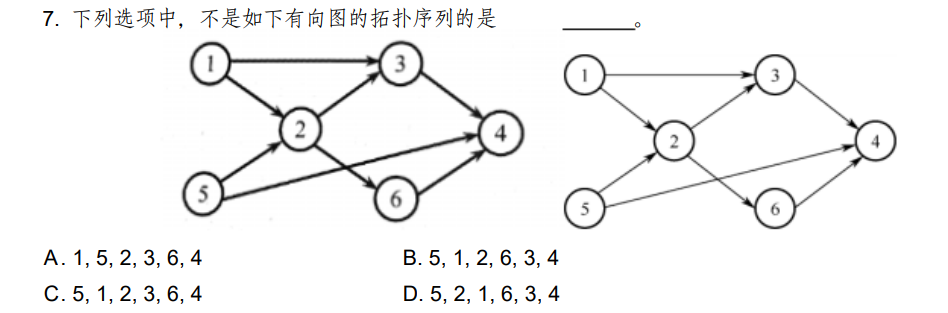
D
2020-6

深搜来写拓扑排序 ,每次到叶节点,即是出度为0的点,遍历也就是相反的顺序