线性回归：
线性：函数(模型)参数的最高次项等于1(这也是数学中线性函数和非线性函数的概念)
回归：最终要求计算出θ值，并选择最优的θ值构成算法公式
?
线性回归：
实质上就是找x和y之间的线性关系，由于x(特征变量)和y(预测值)都是已知的,
那么找的就是的θ最优值
独立：不同样本之间的预测值/误差值是相互独立的，没有任何关系
同分布：一个样本在不同的特征上的误差是同分布的
均值为零: 线性回归的目的是让函数均匀的分布在样本的两侧, 两边的误差值可以正负抵消；
最理想的就是从1-m个样本的误差平方和e等于0(则误差均值e/m也为0)
?
?
?
?
?
** 00:29:03-00:59:37 讲解求解过程
**00:59:00-01:06:39 如何在官网下载案例的训练数据
?最小二乘.py
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split# 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
# 加载数据
path = '../datas/household_power_consumption_1000.txt'
df = pd.read_csv(filepath_or_buffer=path, sep=';')
# 查看一下info信息
# print(df.info())
# print(df.head(5))
# 获取功率的值作为特征属性X，获取电流的值作为目标属性Y
X = df.iloc[:, 2:4]
Y = df.iloc[:, 5]
# print(X.head(5))
# print(Y)
# 将数据分成训练集和测试集
# random_state：随机数种子，保证在分割数据的时候，多次执行的情况，产生的数据是一样的
x_train, x_test, y_train, y_test = train_test_split(X, Y,
train_size=0.8, random_state=0)
print(x_train.shape)
print(type(x_train))
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)
# 模型构建
# 1. 使用numpy的API讲DataFrame转换成为矩阵的对象
x = np.mat(x_train)
y = np.mat(y_train).reshape(-1, 1)
print(y.shape)
print(type(x))
# 2. 求解析式
theta = (x.T * x).I * x.T * y
print(theta)
# 使用模型对数据做预测
y_hat = np.mat(x_test) * theta?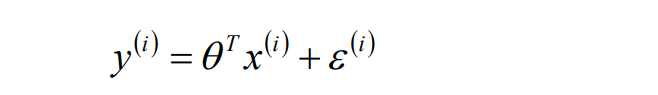
# 画图看一下效果如何
t = np.arange(len(x_test))
plt.figure(facecolor='w')
plt.plot(t, y_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, y_hat, 'g-', linewidth=2, label=u'预测值')
plt.legend(loc='lower right')
plt.title('线性回归')
plt.show()
04_案例代码：使用ScikitLearn相关算法API实现案例代码及机器学习代码编写流程
案例代码：使用ScikitLearn实现普通最小二乘线性回归算法案例代码
?05_案例代码：使用ScikitLearn实现普通最小二乘线性回归算法案例代码讲解
?
**1:52:33-官网上线性回归算法的用法
?
?
?