[数据结构与算法]PAT_1103 Integer Factorization (30 分)(DFS+剪枝)

题目链接


题意还是很好理解的，朴素版本的DFS也是很容易写出的（如169 5 2，第一个基底选12的话，就变成子问题25 4 2了，解决子问题可以递归，第一个基底不断缩小最小到1可以得到其他的情况），K的大小就是dfs 的最深的层次，从大到小枚举基底，基底的上界一开始想的是拿N的根p次方，如169 5 2的话就是从13开始枚举，没有进行剪枝时连样例169 167 3都无法在规定时间跑完，但是提交上去还是能拿23分的，说明陈越姥姥还是很仁慈的。

从中定义了int getFirst(int N)函数，用来获得N的根p次方的值，定义了快速幂kPow(int base,int n)函数计算$bas{e}^n$,这是最开始的思路，进行了下面的4处剪枝/优化： （当然这些值其实可以打表的）

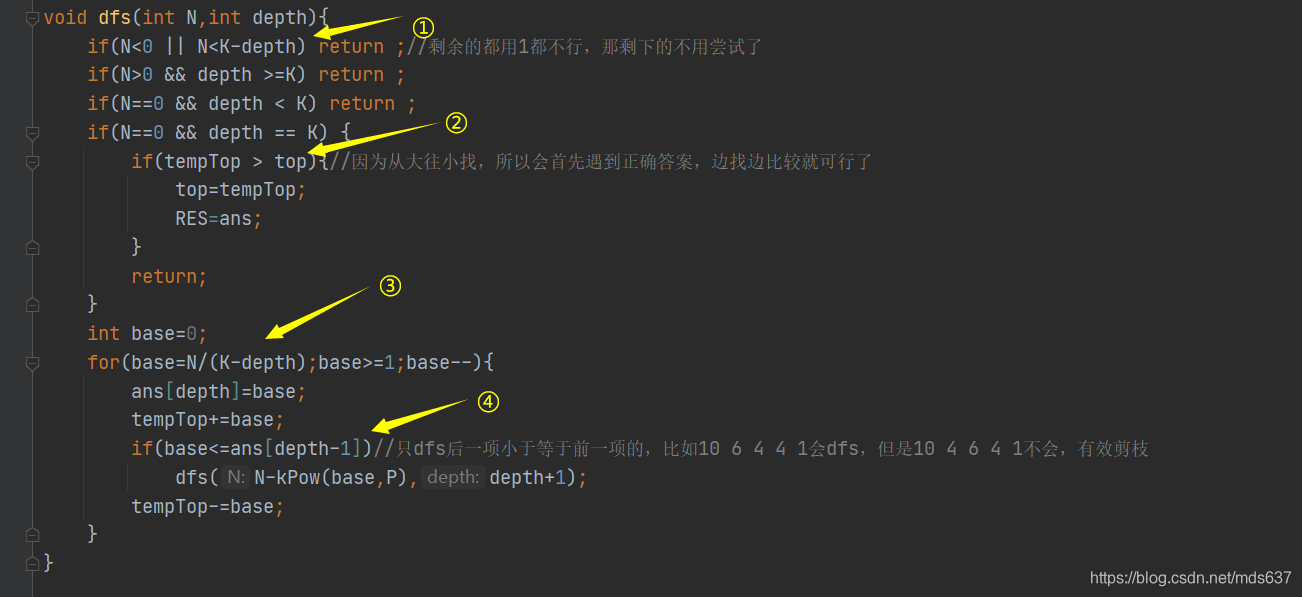
以上四处改动才逐步把分数拿满，第一处的剪枝保证了诸如样例169 167 3这种能过，因为从大的底数进行查找，当$169=5^3+....$, 如果没有这层剪枝，将会一直搜索下去，会$169=5^3+2^3+1^3+1^3....$,但是此时因为125+（167-1）已经超过169了，也就是说剩下的166个空位，全部是$1^3$都不能等于169，更何况程序还会尝试$2^3$,更有甚者会自由组合以下1和2，又会很多情况，但是因为都是没用的情况所以可以减掉。修改之后可以拿到24分/25分 不记得了。
·
·
·
第二处改动解决了样例5和6MLE的问题（成功将测试样例5转为TLE），一开始为了检查dfs的正确性，使用vector< vector < int >>类型的变量存储所有的最终结果，然后再遍历一遍找到符合题意的输出，但是因为有很多使得等式成立的组合，全部存下来会爆内存，鉴于是从大到小的寻找基底，因此可以边比较边存储，因为对于sum相同的情况，肯定首先遇到像6 6 6 6 5这样的情况（因为从大都小寻找基底），因此只要tempTop>top时更新答案即可，不需要先搜到所有答案再进行排序比较，这也说明了要巧妙利用dfs搜索的顺序。
·
·
·
第四处改动
在搜索过程中会出现诸如10 6 4 4 1，10 4 4 6 1， 10 1 4 4 6等，这些无非是这几个数字的自由组合，对最终答案没有影响，因为是从大到小搜索基底的，所以只需要对下一个基底≤上一个基底的基低进行dfs，因为后者大于前者的情况肯定被搜索过了。有了以上三处改动就能保证25分了，只有测试样例5会超时。
·
·
·
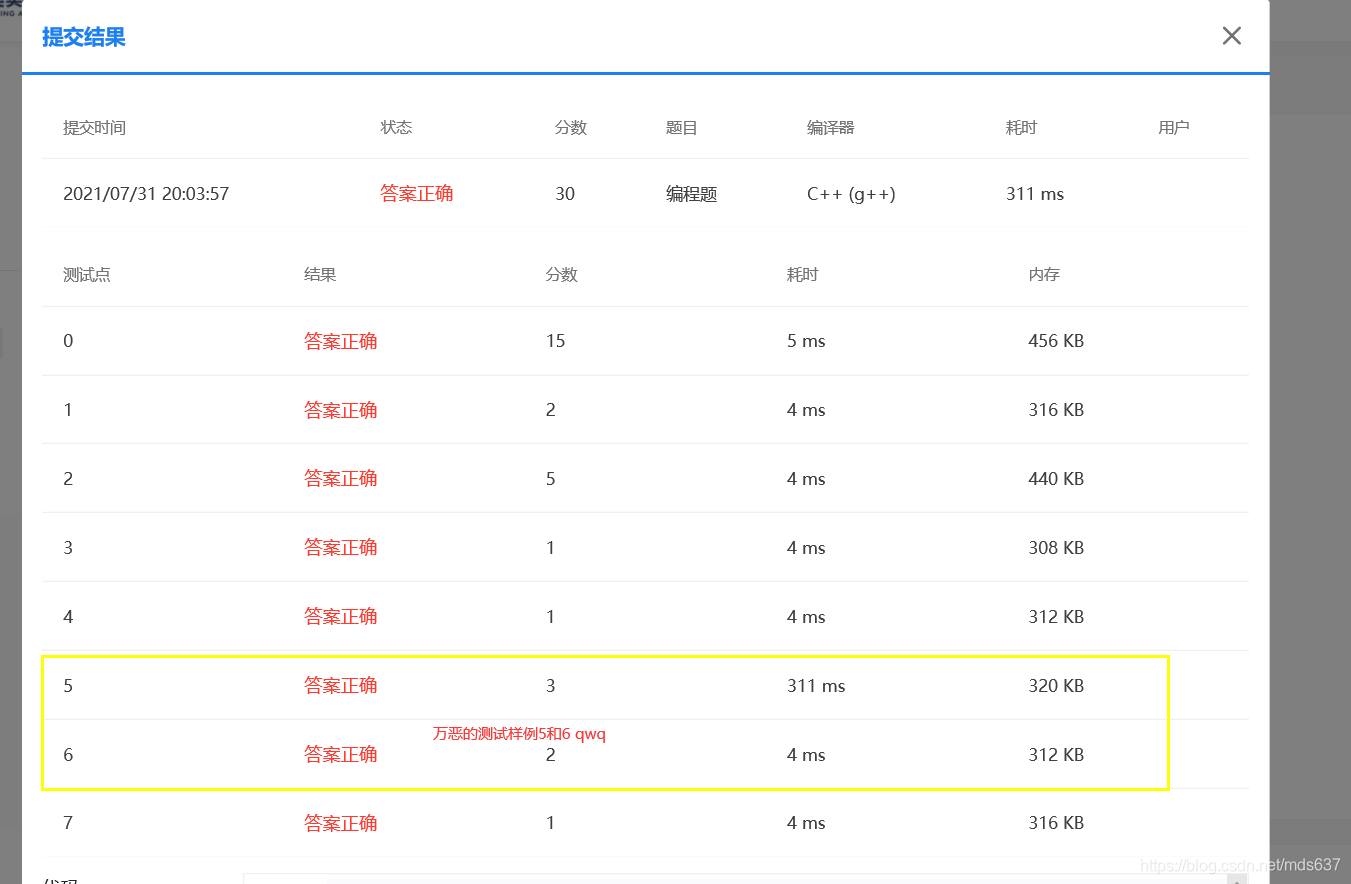
第三处改动解决的最难的测试样例5和6，即拿满30分。一开始写的是base=getFirst(N),这样的开端其实是最大的，对于400 100 2这种，开局就base=17，跑到猴年马月。鉴于答案都是相差不大的数字，因此想到了平均值，让初始base=getFirst(N/K),想着均匀分到N/K,再开p次根号，然后再从大于这个结果的数开始进行查找，这样虽然很完美的解决了400 100 2，但是提交之后只得了3分，说明起点太小了，后来又尝试base=(getFirst(N/K)+getFirst(N))/2也是3分,base=(getFirst(N/K)+2* getFirst(N))/3 (只在main函数修改，dfs中保持getFirst(N))这样能得27分（测试样例6得到2分，测试样例5还是TLE），相应的把dfs中base也改成(getFirst(N/K)+2 *getFirst(N))/3 就只能4分了，这说明可以优化的地方确实是这个起始点，但是这样不断试错肯定考试的时候心态会爆炸啊，于是先出去取快递，在路上想到可不可以直接用N/K作为起点，想了想1<P≤7，P没取到1，而N/K恰好就是K个位置每个位置是N/K的一次方，（N/K,N/K,N/K,N/K,N/K…N/K）这相对于最终的答案也是一个比较大的起点，因为每个位置至少还要平方，加和会大于N，从这个起始点进行搜索，dfs到最深层会从最右边不断缩小基底，不会漏掉可行解，回到家提交果然AC了！开心！可以安心看其他大佬的题解了嘿嘿
值得一提的是，main中base=N/K dfs中base=getFirst(N) 通过测试样例5为1000ms+，main中base=N/K,dfs中base=N/（N-depth）（对于子问题，也是先拿平均值也就是一次方作为寻找的上界）测试样例5就是300ms，可以看到一开始自己找的那个起点有多辣鸡呜呜，改用这种平均值作为起点之后，相应的getFirst()函数的使命也就结束了。

终于AC的代码：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int kPow(int base,int n){//计算base的n次方，快速幂板子
    int ans=1;
    while(n){
        if(n&1==1) ans*=base;
        n=n>>1;
        base=base*base;
    }
    return ans;
}
int K,P;//全局变量，省去dfs的时候传参
vector<int> ans(405,0);
vector<int> RES;//记录最终答案
int getFirst(int N){//求P次根号，恰好开出来取整，否则取第一个小于此数的
    int ans=1;
    for(ans=1;ans<=N;ans++){
        if(kPow(ans,P)>=N)
            break;
    }
    if(kPow(ans,P)==N) return ans;//恰好开出来取整
    else return ans-1;//否则取第一个p次方小于此数的
}

int top=0,tempTop=0;//记录最大值和临时最大值
void dfs(int N,int depth){
    if(N<0 || N<K-depth) return ;//剩余的都用1都不行，那剩下的不用尝试了
    if(N>0 && depth >=K) return ;
    if(N==0 && depth < K) return ;
    if(N==0 && depth == K) {
        if(tempTop > top){//因为从大往小找，所以会首先遇到正确答案，边找边比较就可行了
            top=tempTop;
            RES=ans;
        }
        return;
    }
    int base=0;
    for(base=N/(K-depth);base>=1;base--){//base和main统一起来，对于子问题，也是先拿平均值也就是一次方作为寻找的上界
        ans[depth]=base;
        tempTop+=base;
        if(base<=ans[depth-1])//只dfs后一项小于等于前一项的，比如10 6 4 4 1会dfs，但是10 4 6 4 1不会，有效剪枝
            dfs(N-kPow(base,P),depth+1);
        tempTop-=base;
    }
}

int main() {
    int N;
    cin >> N >> K >> P;
    int depth=0,base=0;
    for(base=N/K;base>=1;base--){//开始用的getFirst(N),测试5会超时,改成N/K才能通过
        ans[depth]=base;
        tempTop+=base;
        dfs(N-kPow(base,P),depth+1);
        tempTop-=base;
    }
    if(top==0) cout << "Impossible";
    else{//按照要求输出
        cout << N << " = ";
        for(int i=0;i<K;i++){
            cout << RES[i] << "^" << P;
            if(i!=K-1){
                cout << " + ";
            }
        }
    }
    return 0;
}