排序算法
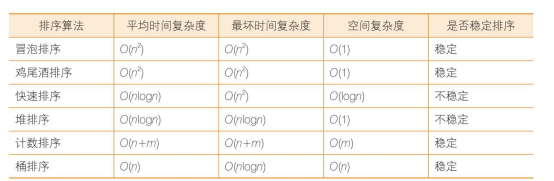
1.时间复杂度为O(n2)的排序算法
-
冒泡排序(bubble sort) 一种基础的交换排序,排序思想:把相邻的元素两两比较,当一个元素大于右侧想领元素时,交换他们的位置;当一个元素小于或等于右侧相邻元素时,位置不变。
冒泡算法是一种稳定排序。
- 鸡尾酒排序:基于冒泡排序的一种升级排序法。鸡尾酒排序的元素比较和交换过程是双向的。排序思想:排序过程就像钟摆一样,第1轮从左到右,第2轮从右到左,第3轮再从左到右…
- 优点:能够在特定条件下,减小排序的回合数,在大部分元素已经有序的情况时,鸡尾酒排序比较有优势。
- 缺点:代码量几乎增加了1倍。
- 鸡尾酒排序:基于冒泡排序的一种升级排序法。鸡尾酒排序的元素比较和交换过程是双向的。排序思想:排序过程就像钟摆一样,第1轮从左到右,第2轮从右到左,第3轮再从左到右…
-
选择排序:不稳定排序
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置;
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾;
- 重复第二步,知道所有元素均排序完成。
-
插入排序:又称直接插入排序,实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
-
希尔排序(略优于O(n2),但有比不上O(nlogn))
2.时间复杂度为O(nlogn)的排序算法
-
快速排序(Quicksort):使用了分治法,排序思想:在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列的一遍,比它小的元素移动到数列的另一边,从而把数列拆解成两个部分。
基准元素(pivot-枢轴; 中心点; 中心; 核心;)的选择以及元素的交换都是快速排序的核心问题。
最坏情况下的时间复杂度是O(n2),平均空间复杂度为 O(logn)。
-
归并排序:利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略。

-
堆排序:最坏时间复杂度稳定为 O(nlogn),空间复杂度为 O(1),排序步骤:
- 把无序数组构建成二叉堆。需要从小到大排序,则构建成最大堆;需要从大到小排序,则构建成最小堆。
- 循环删除堆顶元素,替换到二叉堆的末尾,调整堆产生新的堆顶。
3.时间复杂度为线性的排序算法
-
计数排序:适应于一定范围内的整数排序。排序思想:建立改范围的数组,遍历无需的随机数组,每一个整数按照其值对号入座,同时,对应数组下表的元素进行加1操作。
原始数列的规模是n,最大和最小整数的差值是m,则时间复杂度是 m+n,空间复杂度是 m。
计数排序的局限性:
- 当数列最大和最小值差距过大时,并不适合用计数排序;
- 当数列元素不是整数时,也不适合用计数排序。
-
桶排序:对计数排序的局限性做了弥补。桶(bucket)排序需要创建若干个桶协助排序,每个桶代表一个区间范围,里面可以承载一个或多个元素,桶的区间跨度=(最大值 - 最小值)/(桶的数量 - 1)【数据类型不同,区间跨度和桶数量取值不同】。时间复杂度为 O(n),空间复杂度为 O(n)。最坏时间复杂度为 O(nlogn)。
-
基数排序
**稳定排序和不稳定排序:**如果值相同的元素在排序后仍然保持着排序前的顺序,则这样的排序算法是稳定排序;如果之相同的元素在排序后打乱了排序前的顺序,则这样的排序算法是不稳定排序。