文章目录
1.广度优先搜索 Breadth First Search(BFS)
1.图例
举个例子,对于这张图:

我们想要知道从起点到终点最短需要多少步,采用广度优先搜索的方法:
1.将起点入队。
2.将队首元素向四周可拓展的点入队。如果没有可拓展的点,则说明该点是死路,该元素出队。
3.重复上述步骤,直到到达目标位置或者队列为空。
此过程图示见下图
- 所以,我们先将起点(1,1)入队。
- 再向它的四周试探:向右有路径,向下有路径,向左无路径,向上无路径。即将(1,2)和(2,1)入队,步数记为1,将这两点标记为已访问。
- 再将(1,1)出队。
此时队列内的情况为:
(1,2)点,步数为1
(2,1)点,步数为1
- 再对(1,2)点进行四方向拓展,发现(2,2)点可以拓展,则(2,2)点入队,步数记为2,并将(2,2)点标记为已访问。
- (1,2)点出队。
- 对(2,1)点进行四方向拓展,由于(2,2)点已被访问,无可拓展的点,(2,1)点直接出队。
- …
过程如图所示:

注:此图为方便理解,标注了更多步数,实际程序5步运行到终点就会停止搜索了。
2.c++实现代码
c++语言实现代码如下:
#include <iostream>
#include <stdio.h>
#include <queue>
using namespace std;
int map[100][100], v[100][100]; //map是地图数组,v是访问数组
struct point
{
int x; //行号
int y; //列号
int step; //步数
};
queue<point> r; //申请队列,用于存储各个点和步数
int dx[4] = {0, -1, 0, 1},dy[4] = {1, 0, -1, 0}; //偏移数组,用于向四方向移动
int main()
{
//输入
//n是地图的行数,m是地图的列数,startx,starty是起点坐标,p,q是终点坐标
int n, m, startx, starty, p, q;
printf("请输入地图的行数和列数:");
scanf("%d%d", &n, &m);
printf("请依次输入地图各点情况:\n");
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &map[i][j]);
printf("请依次输入起点横纵坐标,终点横纵坐标:");
scanf("%d%d%d%d", &startx, &starty, &p, &q);
//BFS
//对起点start初始化
point start;
start.x = startx;
start.y = starty;
start.step = 0;
r.push(start); //起点入队
v[startx][starty] = 1; //将起点设置为已访问
int flag = 0; //用来标记是否能到达终点,初值为0
while (!r.empty())
{
//使x,y分别为队首元素的行号和列号
int x = r.front().x, y = r.front().y;
//到终点的情况
if (x == p && y == q)
{
flag = 1; //到达终点则flag变量修改为1
printf("广度搜索结果为:最短路径长度为%d步", r.front().step);
break;
}
//进行四个方向试探
for (int k = 0; k <= 3; k++)
{
//tx,ty是试探的点
int tx, ty;
tx = x + dx[k];
ty = y + dy[k];
//当试探的点无障碍且未访问时
if (map[tx][ty] == 1 && v[tx][ty] == 0)
{
//将该试探点入队
//思路:建立一个新的临时结构体变量,复制该试探点的x,y,和步数,然后将临时变量入队,改试探点标记为已访问 point temp;
temp.x = tx;
temp.y = ty;
temp.step = r.front().step + 1;
r.push(temp);
v[tx][ty] = 1;
}
}
//拓展完毕的队首元素出队
r.pop();
}
if(flag==0) //没有达到终点的情况
printf("无解!\n");
return 0;
}
2.深度优先搜索 Depth First Search(DFS)
1.图例
同样对于这幅图:
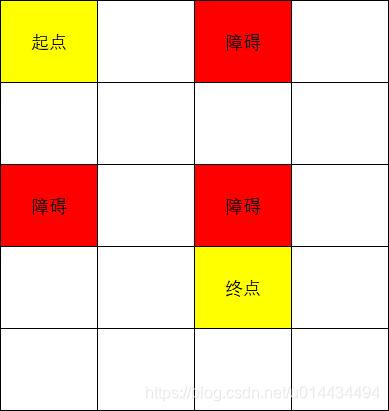
采用广度优先搜索的方法:
对于每一个点,依照顺时针顺序依次对右、下、左、上进行试探,沿着一条路走到底,然后进行回溯到上一个十字路口,试探另一条路……按照这种方法把所有可能性的道路试探完毕。最后取最小的那一个步长。
如下图所示从起点先沿着蓝色路径走到终点,再沿着粉色路径回溯到上一个点、上上个点,走新的岔路进行试探。需要注意的是,每次回溯都要把该点设置为未访问。
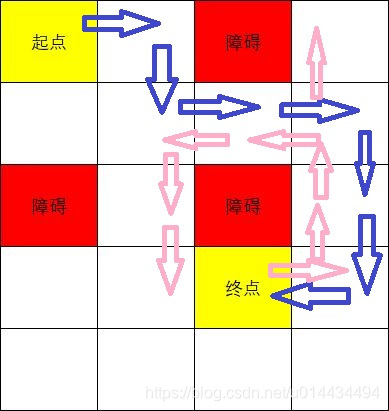
为什么要标记访问的点?
答:防止递归回这个点时候重复调用。
为什么回溯时要取消标记访问过的点?
答:下次通过其他路径去终点的时候可能还会访问到该点。
2.c++实现代码
#include <iostream>
using namespace std;
int p, q, min_step = 9999999; //p,q是终点横纵坐标,最短步长初值为9999999
int map[100][100]; //1表示空地,2表示障碍物
int v[100][100]; //0表示未访问,1表示访问
int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0}; //方向数组
void dfs(int x, int y, int step);
int main()
{
int m, n, startx, starty;
cout << "请输入地图行数、列数:\n";
cin >> m >> n;
cout << "请输入地图情况:\n";
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
cin >> map[i][j];
cout << "请输入起点横纵坐标,终点横纵坐标:\n";
cin >> startx >> starty >> p >> q;
v[startx][starty] = 1;
dfs(startx, starty, 0);
if(min_step==9999999)
cout<<"无法到达终点!";
else
cout << "深度优先搜寻的结果为:最短路径为" << min_step;
return 0;
}
void dfs(int x, int y, int step)
{
if (x == p && y == q)
{
if (step < min_step)
min_step = step;
return;
}
//顺时针试探
for (int k = 0; k <= 3; k++)
{
int tx, ty;
tx = x + dx[k];
ty = y + dy[k];
if (map[tx][ty] == 1 && v[tx][ty] == 0)
{
v[tx][ty] = 1;
dfs(tx, ty, step + 1);
v[tx][ty] = 0;
}
}
return;
}
3.BFS与DFS的对比
一般情况下,广度优先搜索相较于深度优先搜索会更加快地接近目标点,而后中止运行,程序的时间复杂度更低。而深度优先搜索则会完全探索出所有能到达目标点的路径才结束,程序的时间复杂度更高。
因此,最好使用广度优先搜索寻找最短路(最长路同理),深度优先搜索寻找所有路的种数。