[数据结构与算法]动态规划之子序列

动态规划之子序列

不连续子序列

1. “300. 最长递增子序列”

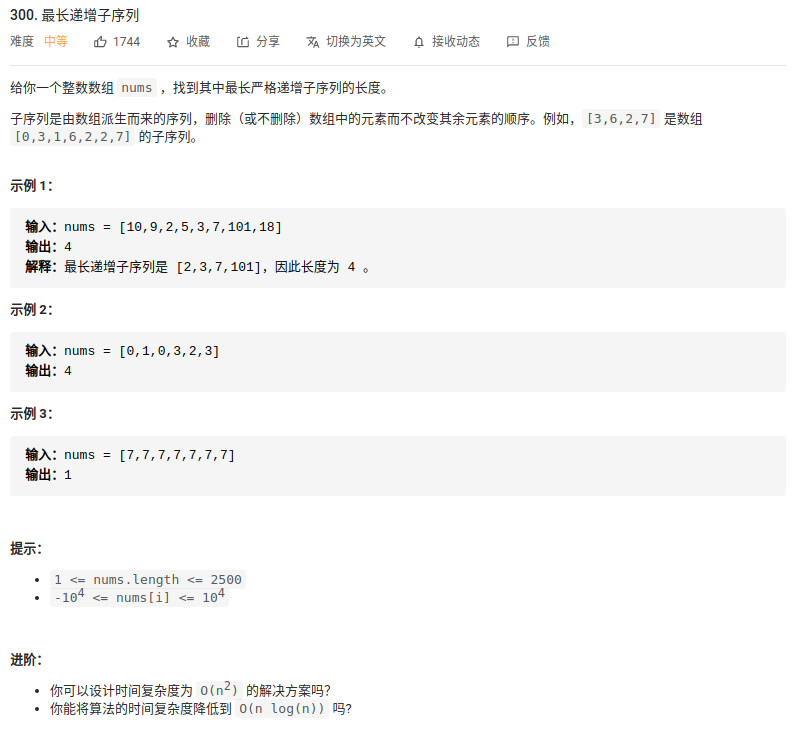
首先定义dp数组的含义：dp[i]代表了包含了数组中第i个数的最大递增子序列的长度，例如在[1,3,6,7,9,4,10,5,6]这个数组中，dp[5]就代表
了子序列[1,3,4]的长度3，而不是最大子序列[1,3,6,7,9]的长度5。要记住dp[i]一定是要包含nums[i]的最大子序列的长度，而不是0到i区间中最大子序列的长度。
为什么要这样定义呢？
我们看[10,9,2,5,3,7,101,18]这个数组，我们先口算一下它的最长递增子序列。

1. nums[0]为10，nums[0]的子序列长度为1
2. nums[1]为9，并且9小于nums[0]，nums[1]的子序列长度为1
3. nums[2]为2，并且2小于nums[1]又小于nums[0]，nums[2]的子序列长度为1
4. nums[3]为5，并且5大于nums[2]，小于nums[1]和nums[0]，因此nums[3]的子序列长度为2
5. nums[4]为3，并且3小于nums[3]，大于nums[2]，小于nums[1]和nums[0]，因此nums[4]的子序列长度为2
6. nums[5]为7，并且7大于nums[4]，nums[3]，nums[2]，取三个中长度最大的+1
   …

大概的思路就是从[0,i-1]中取小于nums[i]的并且子序列长度最大的
这样我们就大概知道状态转移方程了，dp[i] = Math.max(dp[i], dp[j] + 1)，这里j的取值是[0,i-1]

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length < 2) {
            return nums.length;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        Arrays.fill(dp, 1);
        int ans = 0;
        for (int i = 1; i < nums.length; i++) {
            for (int j = i - 1; j >= 0; j--) {
                if (nums[j] < nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

这题只要模拟一下遍历的过程就能很容易的想出状态转移方程来，不过有几个点需要注意一下

1. 因为每个数组的成员本身就是一个子序列，因此需要将dp数组的值初始化为1
2. 在定义dp数组的时候就强调了dp[i]是包含了数组中第i个数的最大递增子序列的长度，而不是0到i区间中最大子序列的长度，因此最终答案应该取dp数组中最大值

2. “1143. 最长公共子序列”

1. 状态定义
   比如对于本题而言，可以定义 dp[i][j] 表示 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列。

2. 状态转移方程
   知道状态定义之后，我们开始写状态转移方程。

当 text1[i - 1] == text2[j - 1] 时，说明两个子字符串的最后一位相等，所以最长公共子序列又增加了 1，所以 dp[i][j] = dp[i - 1][j - 1] + 1；举个例子，比如对于 ac 和 bc 而言，他们的最长公共子序列的长度等于 a 和 b 的最长公共子序列长度 0 + 1 = 1。
当 text1[i - 1] != text2[j - 1] 时，说明两个子字符串的最后一位不相等，那么此时的状态 dp[i][j] 应该是 dp[i - 1][j] 和 dp[i][j - 1] 的最大值。举个例子，比如对于 ace 和 bc 而言，他们的最长公共子序列的长度等于 ① ace 和 b 的最长公共子序列长度0 与 ② ac 和 bc 的最长公共子序列长度1 的最大值，即 1。
综上状态转移方程为：

dp[i][j] = dp[i - 1][j - 1] + 1;
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int t1 = text1.length();
        int t2 = text2.length();
        int[][] dp = new int[t1 + 1][t2 + 1];
        for (int i = 1; i <= t1; i++) {
            for (int j = 1; j <= t2; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return dp[t1][t2];
    }
}

3. “1035. 不相交的线”

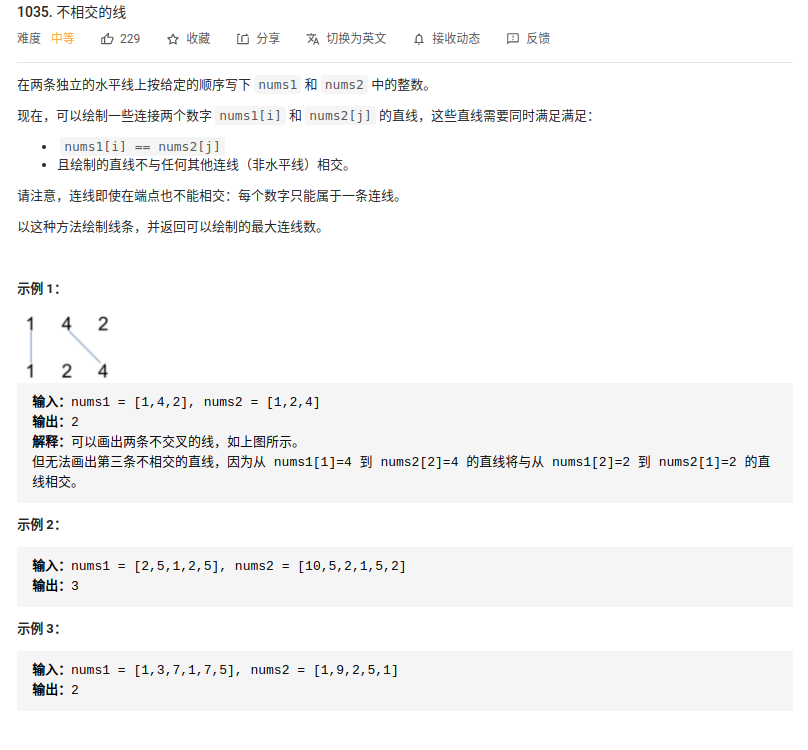
与上题思路一样，dp[i][j]代表nums1[0:i]和nums2[0:j]的最大不相交的连接数

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int l1 = nums1.length;
        int l2 = nums2.length;
        int[][] dp = new int[l1 + 1][l2 + 1];
        for (int i = 1; i <= l1; i++) {
            for (int j = 1; j <= l2; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[l1][l2];
    }
}

连续子序列

4. “674. 最长连续递增序列”

这题思路与“300. 最长递增子序列”差不多，只不过这题要求的是连续的，只需要比较nums[i]与nums[i-1]即可

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        if (nums.length == 1) {
            return 1;
        }
        int[] dp = new int[nums.length];
        Arrays.fill(dp, 1);
        int ans = 0;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]) {
                dp[i] = Math.max(dp[i], dp[i - 1] + 1);
            }
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

5. “718. 最长重复子数组”

这题和"1143. 最长公共子序列"思路差不多，只不过这题的要求是连续的子数组。那么思考一下，如果要求返回连续的数组，当nums[i]=nums[j]就去判断nums[i-1]是否等于nums[j-1]，那么dp[i][j] = dp[i - 1][j - 1] + 1这个状态转移方程一定是成立的，那么如果nums[i]!=nums[j]，那么nums[i][j]=0。

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int l1 = nums1.length;
        int l2 = nums2.length;
        int[][] dp = new int[l1 + 1][l2 + 1];
        int ans = 0;
        for (int i = 1; i <= l1; i++) {
            for (int j = 1; j <= l2; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                ans = Math.max(ans, dp[i][j]);
            }
        }
        return ans;
    }
}

6. “53. 最大子序和”

先模拟一下数组遍历过程，因为是求最大和的连续子数组，因此只需要将nums[i]和加上nums[i]的和相比较就行了。也就是说如果加上nums[i]比较大，dp[i]就等于加上nums[i]的和,如果加上nums[i]的和比nums[i]小，那么和就是nums[i]。
那么就可以得到dp[i]的定义，dp[i]代表加上nums[i]的最大和
状态转移方程为dp[i] = Math.max(nums[i], dp[i - 1] + nums[i])

class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 1) {
            return nums[0];
        }
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int ans = Integer.MIN_VALUE;
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
            ans = Math.max(ans, dp[i]);
        }
        ans = Math.max(ans, dp[0]);
        return ans;
    }
}

编辑距离

7. “115. 不同的子序列”

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QNSCzKNS-1627832797208)(https://z3.ax1x.com/2021/07/31/Wvf3se.png)]
dp数组含义：dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
递推公式：

class Solution {
    public int numDistinct(String s, String t) {
        int sl = s.length();
        int tl = t.length();
        int[][] dp = new int[tl + 1][sl + 1];
        for (int i = 0; i <= sl; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i <= tl; i++) {
            dp[i][0] = 0;
        }
        for (int i = 1; i <= tl; i++) {
            for (int j = 1; j <= sl; j++) {
                if (t.charAt(i - 1) == s.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];
                } else {
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
        return dp[tl][sl];
    }
}

8. “583. 两个字符串的删除操作”

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7UqvfyrP-1627832797209)(https://z3.ax1x.com/2021/08/01/WzLsPO.png)]
dp数组定义：dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。
递推公式：当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：
情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
初始化：dp[i][0]：word2为空字符串，以i-1为结尾的字符串word2要删除多少个元素，才能和word1相同呢，很明显dp[i][0] = i。
dp[0][j]的话同理

class Solution {
    public int minDistance(String word1, String word2) {
        int word1Length = word1.length();
        int word2Length = word2.length();
        int[][] dp = new int[word1Length + 1][word2Length + 1];
        for (int i = 0; i <= word1Length; i++) {
            dp[i][0] = i;
        }
        for (int i = 0; i <=word2Length; i++) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= word1Length; i++) {
            for (int j = 1; j <= word2Length; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1), dp[i][j - 1] + 1);
                }
            }
        }
        return dp[word1Length][word2Length];
    }
}

9. “72. 编辑距离“

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Zj3w3X3u-1627832797210)(https://z3.ax1x.com/2021/08/01/WzOVdx.png)]
dp数组含义：dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。
递推公式：if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1]
if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？
操作一：word1增加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 加上一个增加元素的操作。
即 dp[i][j] = dp[i - 1][j] + 1;
操作二：word2添加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个增加元素的操作。
即 dp[i][j] = dp[i][j - 1] + 1;
操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。
即 dp[i][j] = dp[i - 1][j - 1] + 1;
综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
那么dp[i][0] 和 dp[0][j] 表示什么呢？
dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;
同理dp[0][j] = j;

class Solution {
    public int minDistance(String word1, String word2) {
        int word1Length = word1.length();
        int word2Length = word2.length();
        int[][] dp = new int[word1Length + 1][word2Length + 1];
        for (int i = 0; i <= word1Length; i++) {
            dp[i][0] = i;
        }
        for (int i = 0; i <= word2Length; i++) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= word1Length; i++) {
            for (int j = 1; j <=word2Length; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1] + 1, dp[i - 1][j] + 1), dp[i][j - 1] + 1);
                }
            }
        }
        return dp[word1Length][word2Length];
    }
}

回文

10. “516. 最长回文子序列”

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-829PRxx1-1627832797210)(https://z3.ax1x.com/2021/08/01/fSETHK.png)]
dp数组定义：dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
递推公式：如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
初始化：首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
遍历顺序：从递推公式dp[i][j] = dp[i + 1][j - 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 可以看出，dp[i][j]是依赖于dp[i + 1][j - 1] 和 dp[i + 1][j]，
也就是从矩阵的角度来说，dp[i][j] 下一行的数据。 所以遍历i的时候一定要从下到上遍历，这样才能保证，下一行的数据是经过计算的。

class Solution {
    public int longestPalindromeSubseq(String s) {
        int[][] dp = new int[s.length()][s.length()];
        for (int i = s.length() - 1; i >= 0; i--) {
            dp[i][i] = 1;
            for (int j = i + 1; j < s.length(); j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2; 
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j],dp[i][j - 1]);
                }
            }
        }
        return dp[0][s.length() - 1];
    }
}

11. “647. 回文子串”

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3PS0Mslj-1627832797211)(https://z3.ax1x.com/2021/08/01/fSE2h4.png)]
dp数组定义：布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。
递推公式：整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。
当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况
情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
遍历顺序：在对dp[i][j]进行赋值true，是根据dp[i + 1][j - 1]是否为true，dp[i + 1][j - 1] 在 dp[i][j]的左下角，所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

class Solution {
    public int countSubstrings(String s) {
        int ans = 0;
        boolean[][] dp = new boolean[s.length()][s.length()];
        for (int i = s.length() - 1; i >= 0; i--) {
            for (int j = i; j < s.length(); j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    if (j - i <= 1) {
                        ans++;
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) {
                        ans++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return ans;
    }
}

12. “5. 最长回文子串”

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-avp8UttW-1627832797212)(https://z3.ax1x.com/2021/08/01/fSVfIS.png)]

class Solution {
    public String longestPalindrome(String s) {
        boolean[][] dp = new boolean[s.length()][s.length()];
        int max = -1;
        int left = 0;
        int right = 0;
        for (int i = s.length() - 1; i >= 0; i--) {
            for (int j = i; j < s.length(); j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    if (j - i <= 1) {
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) {
                        dp[i][j] = true;
                    }
                    if (j - i > max && dp[i][j]) {
                        max = j - i;
                        left = i;
                        right = j;
                    }
                }
            }
        }
        return s.substring(left, right + 1);
    }
}

与上题思路类似，不过需要记录j-i最大的情况，j-i最大且dp[i][j]=true即为回文子串时，就为结果