给你一棵二叉树,请你返回满足以下条件的所有节点的值之和:
该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。)
如果不存在祖父节点值为偶数的节点,那么返回?0 。
示例:
?
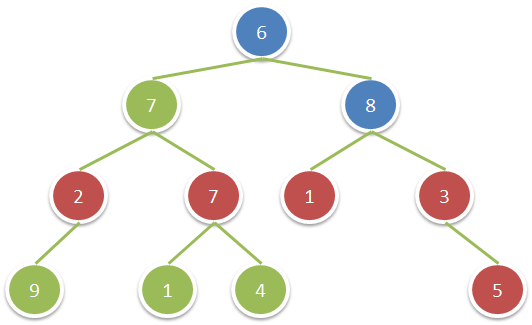
输入:root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出:18
解释:图中红色节点的祖父节点的值为偶数,蓝色节点为这些红色节点的祖父节点。
?
提示:
树中节点的数目在?1 到?10^4?之间。
每个节点的值在?1 到?100 之间。
方法写在注释里面,基本思路就是先深度优先搜索一次记录祖父节点。
然后宽度优先搜索,算出孙子节点的和。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution {
public:
int sumEvenGrandparent(TreeNode* root) {
int result = 0;
vector<TreeNode*> fV;
recordEven(root, fV);
for (int i = 0; i < fV.size(); i++) {
BFS(fV[i], result);
}
return result;
}
private:
/* 祖父节点进行层次遍历,使用队列,result孙子节点的和 */
void BFS(TreeNode* root, int& result) {
int deepCount = 1; //记录层数
queue<TreeNode*> tQue;
tQue.push(root);
while (!tQue.empty()) {
/* 大于3层,没必要往下继续遍历,因为已经得到了孙子节点 */
if (deepCount > 3) {
break;
}
int count = tQue.size();
while (count--) {
TreeNode* front = tQue.front();
/* 此时计算的是祖父节点的孙子节点,将每一层的孙子节点值相加 */
if (deepCount == 3) {
result += front->val;
}
if (front->left) {
tQue.push(front->left);
}
if (front->right) {
tQue.push(front->right);
}
tQue.pop();
}
deepCount++;
}
}
private:
/*
* 记录偶数的祖父节点,这个地方应该还可以优化的,因为深度搜索,
* 搜索到叶子节点的往上两层,没必要再搜索,因为不可能为祖父节点。
* 暂时没想到方法,先这样把。
*/
void recordEven(TreeNode* root, vector<TreeNode*>& fV) {
if (root == NULL) {
return;
}
if (root->val % 2 == 0) {
fV.push_back(root);
}
if (root->left) {
recordEven(root->left, fV);
}
if (root->right) {
recordEven(root->right, fV);
}
}
};