[数据结构与算法]面试题七：重建二叉树（正式题解：给出二叉树的前序遍历序列和中序遍历序列 重建出 二叉树）

• 题目：输入某二叉树的前序遍历结果和中序遍历结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复数字。例如前序排列为{1，2，4，7，3，5，6，8}，中序排列为{4，7，2，1，5，3，8，6}
• 分析：
  下图为需要重建的二叉树：

			                   1
			                  / \
			                 2   3
			                /    /\
			               4    5  6
			                \      /
			                 7    8

关键点为需要搞清：得出前序排列的方式为利用递归和打印节点相结合，具体代码如下：

void PrintTree(const BinaryTreeNode* pRoot) {
    PrintTreeNode(pRoot);

    if (pRoot != nullptr)
    {
        if (pRoot->m_pLeft != nullptr)
            PrintTree(pRoot->m_pLeft);

        if (pRoot->m_pRight != nullptr)
            PrintTree(pRoot->m_pRight);
    }
}

根据递归的顺序易知，以上代码先打印输出左节点，到头后，打印最后一个右节点，最后碰到nullptr开始回归。此为前序遍历。
下面来看一下中序遍历代码：

void PrintTree(const BinaryTreeNode* pRoot) {
    if (pRoot != nullptr)
    {
        if (pRoot->m_pLeft != nullptr)
            PrintTree(pRoot->m_pLeft);
            
        PrintTreeNode(pRoot);
        
        if (pRoot->m_pRight != nullptr)
            PrintTree(pRoot->m_pRight);
    }   
}

不难发现，中序遍历只是将打印节点的操作放在了两个if语句中间，先调用到没有左子节点的位置，然后从右节点进行调用一次，在调用左节点，直到最后右节点也为nullptr为止，然后开始回归，遇到有左子节点的打印当前子节点，然后打印右节点…如此进行递归算法，此种打印最终得到中序排序。此处逐行跟踪一下程序就可以很好的理解。
后序打印当然也很好类比了。

• 正式题解的代码如下：
  辅助函数代码：

BinaryTreeNode* Construct(int* preorder, int* inorder, int length) {
    if (preorder == nullptr || inorder == nullptr || length <= 0)
        return nullptr;
    return ConstructCore(preorder, preorder + length - 1,
        inorder, inorder + length - 1);
}

BinaryTreeNode* ConstructCore(int* startPreorder, int* endPreorder,
    int* startInorder, int* endInorder) {
    int rootValue = startPreorder[0];
    BinaryTreeNode* root = new BinaryTreeNode();
    root->m_nValue = rootValue;
    root->m_pLeft = root->m_pRight = nullptr;

    if (startPreorder == endPreorder) {
        if (startInorder == endInorder &&
            *startPreorder == *startInorder)
            return root;
        else
            throw std::exception("Invalid input.");
    }

    //在中序遍历中找到根节点的值
    int* rootInorder = startInorder;
    while (rootInorder < endInorder && *rootInorder != rootValue)
        rootInorder++;

    if (rootInorder == endInorder && *rootInorder != rootValue)
        throw std::exception("Invalid input.");

    int leftLength = rootInorder - startInorder;
    int* leftPreorderEnd = startPreorder + leftLength;
    if (leftLength > 0) {
        //构建左子树
        root->m_pLeft = ConstructCore(startPreorder + 1,
            leftPreorderEnd, startInorder, rootInorder - 1);
    }
    if (leftLength < endPreorder - startPreorder) {
        //构建右子树
        root->m_pRight = ConstructCore(leftPreorderEnd + 1,
            endPreorder, rootInorder + 1, endInorder);
    }
    return root;
}

main.cpp

#include"BinaryTree.h"

int main() {
	const int length = 8;
	int preorder[length] = { 1, 2, 4, 7, 3, 5, 6, 8 };
	int inorder[length] = { 4, 7, 2, 1, 5, 3, 8, 6 };

	BinaryTreeNode* root = Construct(preorder, inorder, length);

	PrintTree(root);

	DestroyTree(root);
}

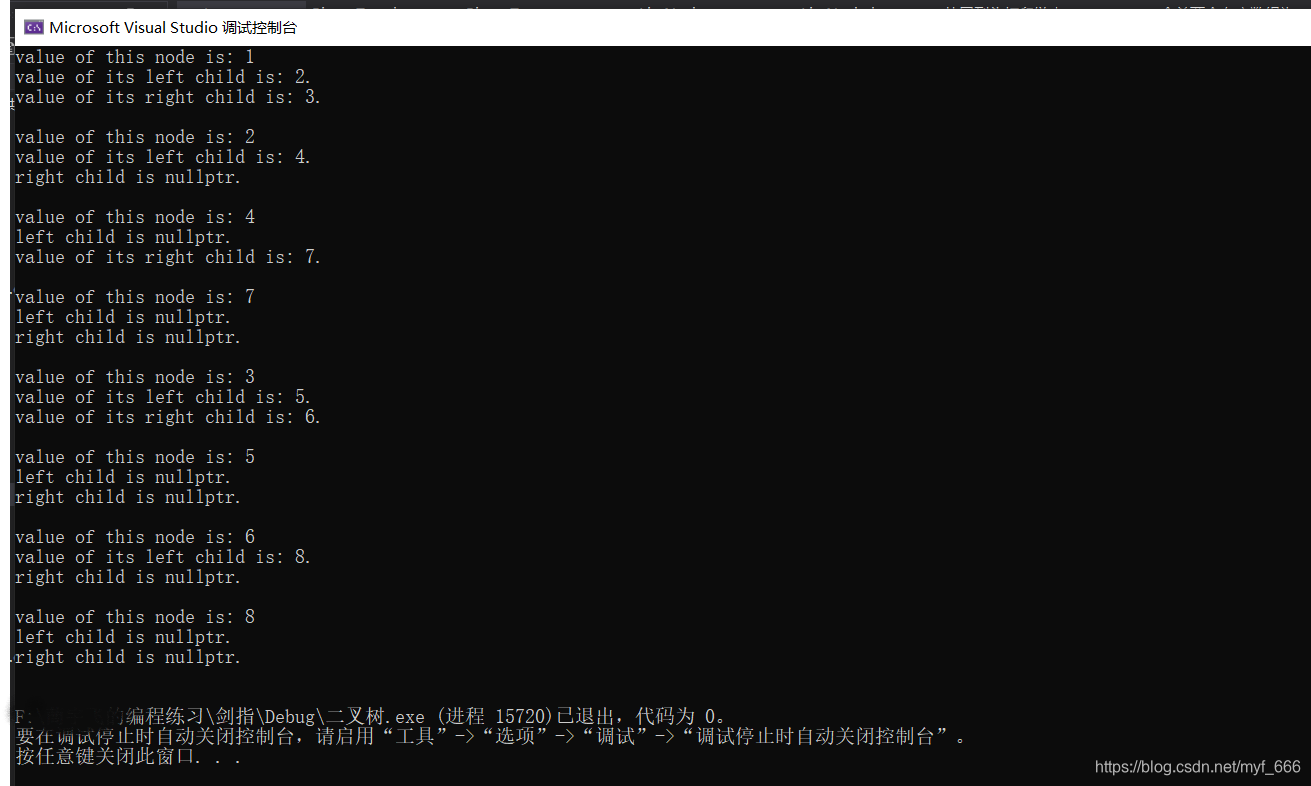
输出结果如下：

欢迎各位点赞评论，一起交流，共同进步！