[数据结构与算法]冉宝的leetcode笔记--每日一题

知道好多人都写了一千+的leetcode才去面试字节，自己确实还有很多需要进步的地方，每天做五题，然后学习2h深度学习，持续进步，加油。

8月1日 – 动态规划

题目198：打家劫舍

链接：https://leetcode-cn.com/problems/house-robber/
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 400

自己的解题思路：

代码：

class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) <=2:
            return max(nums)
        
        dp = [num for num in nums]
        dp[2] = dp[0] + nums[2]
        max_value = max(dp[0:3])
        for i in range(3,len(nums)):
            dp[i] = nums[i] + max(dp[i-2],dp[i-3])
            max_value = max(max_value,dp[i])
        return max_value

ps:官方题解思想:
分情况讨论：
dp[i] 偷到第i家时可以获得最大金额。

• 偷第i家，最大金额为dp[i-2]+nums[i]
• 不偷第i家，最大金额为dp[i-1]
  更新方程： dp[i] = max(dp[i-2]+nums[i],dp[i-1])
  因为滚动数组，可以只用两个数。

题目213：打家劫舍||

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

示例 1：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2：

输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
     偷窃到的最高金额 = 1 + 3 = 4 。

思路： 题目的唯一区别就在于需要记住一个状态，不能首尾同时偷。所以可以有两条链路，

• 第一条：偷了第一家，就可以一直偷到倒数第二家，可以认为和题目198一样，只是最后少了一个房子
• 第二条：没偷第一家，那就可以一直偷到最后一家，可以认为和题目198一样，只是最开始少了一个房子
  返回更大的一个。
  边界：房子数量<=3 ,直接返回最大的一个。
  需要注意初始化的时候也需要用到max
  

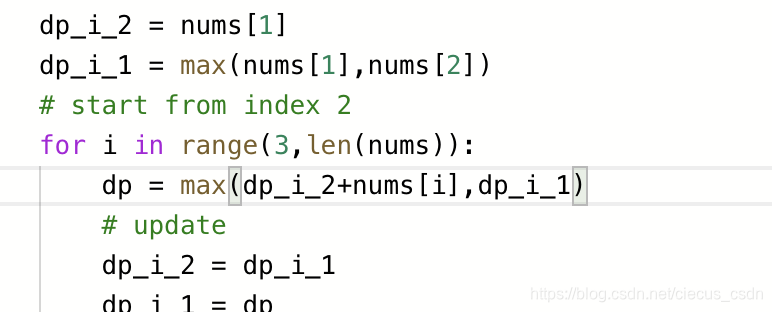
– 借用上一题官方题解的思想。用滚动数组+ 到第i家可以偷到的最大的金额。

740. 删除并获得点数

https://leetcode-cn.com/problems/delete-and-earn/

给你一个整数数组nums，你可以对它进行一些操作。

每次操作中，选择任意一个nums[i]，删除它并获得 nums[i]的点数。之后，你必须删除 所有 等于nums[i] - 1 和 nums[i] + 1的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

示例 1：

输入：nums = [3,4,2]
输出：6
解释：
删除 4 获得 4 个点数，因此 3 也被删除。
之后，删除 2 获得 2 个点数。总共获得 6 个点数。

示例 2：

输入：nums = [2,2,3,3,3,4]
输出：9
解释：
删除 3 获得 3 个点数，接着要删除两个 2 和 4 。
之后，再次删除 3 获得 3 个点数，再次删除 3 获得 3 个点数。
总共获得 9 个点数。

思路：
初始想法：首先可以看作一个集合题 但是不对，观察示例2，就知道一个数字可以使用多次。
因为数字范围很固定：1 <= nums[i] <= $10^4$
不妨构思成，这是一个已经排过序的数组第i个元素为[数字i，数字i的数量]

动态规划数组dp[i]可以构思为：选择数字i可以获得的点数。
因为选择数字i，意味着数字i-1没选。即

– 继续思考，这道题和小偷很像，删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。,就相当于我偷了nums[i]的财富，就不能拥有nums[i] - 1 和 nums[i] + 1的财富。

其中 nums[i]的财富为 nums[I] * 数量。

– 这道题的难点可能在于用什么数据结构比较合适。

我自己的思路： hash + 有序数组
hash记录数字数量num_dict，有序数组sorted_nums用于快速迭代。

新数字new_num,索引为ind出来的更新模式
if sorted_nums[ind-1] == new_num - 1：
dp[ind] = max(dp[ind - 2]+ new_numnum_dict[new_num],dp[ind - 1])
else:
dp[ind] = dp[ind - 1] + new_numnum_dict[new_num]

边界：
num_dict之后：
sorted_nums：
只有一个数字的之后，return num_dict[num]*num
只有两个数字 return max(num_dict[num]*num) - 初始化的细节需要注意

from collections import Counter
class Solution:
    def deleteAndEarn(self, nums: List[int]) -> int:
        num_dict = Counter(nums)
        sorted_nums = sorted(list(num_dict.keys()))
        if len(sorted_nums) == 1: 
            num = sorted_nums[0] 
            return num_dict[num]*num 
        
        dp = [num_dict[num]*num for num in sorted_nums]
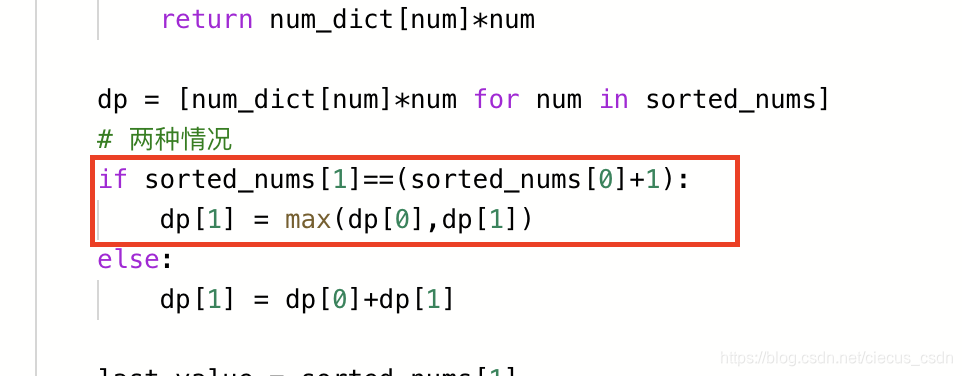
        # 两种情况
        if sorted_nums[1]==(sorted_nums[0]+1):
            dp[1] = max(dp[0],dp[1])
        else:
            dp[1] = dp[0]+dp[1]

        last_value = sorted_nums[1]
        for ind,new_num in enumerate(sorted_nums[2:],start=2):
            if last_value == (new_num-1):
                if dp[ind-2]+new_num*num_dict[new_num] > dp[ind-1]:
                    dp[ind] = dp[ind-2]+new_num*num_dict[new_num]
                    last_value = new_num
                else:
                    dp[ind] = dp[ind-1]
            else:
                dp[ind] = dp[ind-1]+new_num*num_dict[new_num]
                last_value = new_num 
        return dp[-1]

• 也可以改成滑动数组的形式–完成了

55. 跳跃游戏

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

做题时间：2:26-2:39 共计13min
思路：
一开始觉得可以通过bfs做，
思路：

1- 一个变量数组stack：记录这一步可以到达的点
2- 一个变量集合visited：记录已经到过的点
3- 一个变量 last_index

算法思路：

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        visited = set()
        last_index = len(nums)-1
        stack = [0]
        while stack:
            ind = stack.pop()
            if ind== last_index:
                return True
            visited.add(ind)
            step = nums[ind]
            for next_node in range(ind,ind+step+1):
                if next_node == last_index:
                    return True
                if next_node not in visited:
                    stack.append(next_node)
        return False

时间复杂度： O(n*2) 涉及两层遍历
空间复杂度： O(n),需要栈和集合记录会到达的点以及到过的点。

然后想到是连续数组，可以通过滑动窗口的思想思考，
通过dp记录到nums[i]这个位置的时候，能到达的最远的下标：，更新方程：

1. dp[i-1] <i ,无法到达nums[i]的点，return False
2. dp[i] = max(dp[i-1],i+nums[i]) if dp[i] > last_index return True

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        """
        dp[i] 到nums[i] 能到的最远位置的下标
        1- dp[i-1]<i: 到不了，return False
        2- dp[i] = max(dp[i-1],i+nums[i])
        """
        # 可以使用滚动数组
        dp_i_1 = nums[0]
        last_index = len(nums)-1
        for ind,num in enumerate(nums[1:],start=1):
            if dp_i_1 < ind: return False 
            dp = max(ind+nums[ind],dp_i_1)
            if dp >= last_index: return True  
            dp_i_1 = dp 
        return dp_i_1>=last_index

时间复杂度： O(n) 涉及一次遍历
空间复杂度： O(1),滚动数组。

45. 跳跃游戏 II

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

时间：3:00–3:13
思路： 这道题的区别就在于假设你总是可以到达数组的最后一个位置。再有就是需要知道最少跳几次。
思路：不是依次更新dp，
或者： dp[i] 跳到nums[i]的位置需要的最少步数
更新策略： 每次会更新位置dp[i,i+nums[i]] 位置的数字 – 注意右边界
位置j的更新策略:
1- dp[j]没有值，直接写入
2- dp[j] = min(dp[i]+1,dp[j])
然后 return dp[-1]

时间复杂度： O(n*2) 涉及两层遍历
空间复杂度： O(n),需要栈和集合记录会到达的点以及到过的点。

class Solution:
    def jump(self, nums: List[int]) -> int:
        dp = [None for num in nums]
        dp[0] = 0 
        last_index = len(nums)-1
        for i in range(last_index):
            if nums[i] == 0:
                continue
            for j in range(i+1,min(i+nums[i]+1,last_index+1)):
                if not dp[j]:
                    dp[j] = dp[i] +1
                else:
                    dp[j] = min(dp[j],dp[i] +1)
        return dp[-1]

如果做思路改进：从3:29- 3:50 [要注意及时跳出]
就是如果位置i <j <k , 从i 能一步走到k，那么从i->k的步数一定 <= j->k 的步数。
如果还是用dp记录能到的最大右边界。

按照i 从 i+1->i+nums[i] 移动，记录 i+nums[i] 的最大值为这次移动的右边界，边界+1 step加一。

所以还是记录同样步数的最大右边界。
时间复杂度： O(n) 涉及一次遍历
空间复杂度： O(1),滚动数组。

class Solution:
    def jump(self, nums: List[int]) -> int:
        if len(nums)==1: return 0

        last_index = len(nums)-1
        step = 1
        point = 1 
        right_arrow = nums[0]
        if right_arrow >= last_index: return step

        new_right_arrow=right_arrow

        while point < last_index:
            while point <= right_arrow:
                new_right_arrow = min(max(new_right_arrow,point+nums[point]),last_index)
                point += 1 
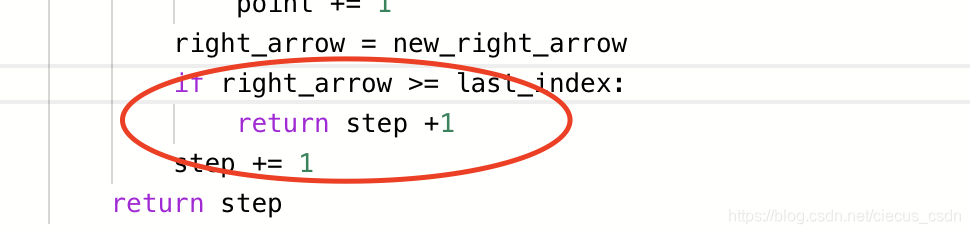
            right_arrow = new_right_arrow
            if right_arrow >= last_index: 
                return step +1
            step += 1
        return step  

step卡在这里了一直算不对，诶。

53.最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [0]
输出：0

示例 4：

输入：nums = [-1]
输出：-1

示例 5：

输入：nums = [-100000]
输出：-100000

用时：8:30- 8:38
思路：
使用滚动数组和max节约内存
时间复杂度o(n) ,空间复杂度o(1)
dp[i] 以nums[i]结尾的最大子序列和
转移公示：
dp[i] = max(0,dp[i-1]) + nums[i]
边界条件：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        # 数组为空
        if not nums:
            return 0
        # 数组负数要不要选择
        if len(nums) ==1:
            return nums[0]

        # 边界条件
        dp_i_1 = nums[0]
        max_v = dp_i_1 

        for num in nums[1:]:
            dp = max(0,dp_i_1) + num
            max_v = max(max_v,dp)
            dp_i_1 = dp 
        return max_v

【第一遍不会做】918.环形子数组的最大和

给定一个由整数数组 A 表示的环形数组 C，求 C 的非空子数组的最大可能和。

在此处，环形数组意味着数组的末端将会与开头相连呈环状。（形式上，当0 <= i < A.length 时 C[i] = A[i]，且当 i >= 0 时 C[i+A.length] = C[i]）

此外，子数组最多只能包含固定缓冲区 A 中的每个元素一次。（形式上，对于子数组 C[i], C[i+1], …, C[j]，不存在 i <= k1, k2 <= j 其中 k1 % A.length = k2 % A.length）
示例 1：

输入：[1,-2,3,-2]
输出：3
解释：从子数组 [3] 得到最大和 3

示例 2：

输入：[5,-3,5]
输出：10
解释：从子数组 [5,5] 得到最大和 5 + 5 = 10

示例 3：

输入：[3,-1,2,-1]
输出：4
解释：从子数组 [2,-1,3] 得到最大和 2 + (-1) + 3 = 4

示例 4：

输入：[3,-2,2,-3]
输出：3
解释：从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3

示例 5：

输入：[-2,-3,-1]
输出：-1
解释：从子数组 [-1] 得到最大和 -1

解法一：动态规划

用时：8:40- 9:21 – 没有做出来
思路：
需要记住dp是从哪里开始的，
可以先看成不是环形的
dp[i] = (start,value) 以nums[I]结尾的最大和
最后的结果一共有两种可能：
（1） 非环形的最大值，就和之前一样的思路 – 如果是0 开始的没有疑问
（2）环形的最大值，如果出现首尾相接的情况，一定是因为中间有个特别大的负值，导致累计和为负数了，即结尾的起始位置不是0。
– 而且结尾的和为正数。
– 也就是结尾的最大值 + start为0的最大值。 – 需要记住。
遗留场景： 第一个数是负数，后面是正的，链接起来更大

需要测试的样例：

• [-1,2,-4,5] --> 输出6
• [6,-1,-1,-1] --> 输出6
• [6,7,-1,-1,-1] --> 输出13
• [6,5,4,-1,-1,-9] --> 输出15
• [6,-5,4,-1,-1,-9] --> 输出6
• [6,2,-10,4,-1,-1,9] --> 输出19
• [4,-5,100,-200,9] --> 输出108
• [-4,-5,100,4,-200,9] --> 输出108

结果还是错了：错的案例：

[5,-3,5]

阅读官方题解的笔记：https://leetcode-cn.com/problems/maximum-sum-circular-subarray/solution/huan-xing-zi-shu-zu-de-zui-da-he-by-leetcode/

方法一： 核心：**kadane算法：**找到A的最大子段和，-- 只考虑非空子段。
dp[j+1]=A[j+1]+max(dp[j],0)-- ps这个我也会。

难点： 使用 Kadane 算法，我们知道如何计算一个单区间子段的最大值，所以剩下的问题是双区间子段。

时间复杂度：O(N), 其中N是A的长度
空间复杂度：O(N)
– 这个解法也没看懂，又耽误了一小时，难过的抄代码：
– 注意边界，我是被o(N)复杂度误导了，官方题解也构建了好多个动态。

class Solution:
   def maxSubarraySumCircular(self, nums: List[int]) -> int:
       # 单区间数组
       max_v = cur = nums[0]

       for x in nums[1:]:
           cur = x + max(cur,0)
           max_v = max(max_v,cur)

       # 逆向取和
       # 先不用滚动数组，就直接dp两个数
       dp2 = [num for num in nums]
       max_right = [num for num in nums]
       # 更新方程
       for ind in range(len(nums)-2,-1,-1):
           dp2[ind] = dp2[ind+1] + nums[ind] 
           max_right[ind] = max(max_right[ind+1],dp2[ind])

       
       # 对[0:start] 段重新算累计和,可以用滚动数组
       left_sum = 0
       for ind,num in enumerate(nums[:-2]): #
           left_sum += num 
           max_v = max(max_v,left_sum + max_right[ind+2])
       return max_v

收获：dp更新的简洁写法，还有就是可以o(n)也可以构建多个dp。

解法优化：

看了官方题解下面的思路，有个想法特别妙。

• 单区间的就还是原来的做法
• 双区间两边最大然后聚合可以做优化，就当于定值和，然后从中间找到最小值，然后剪掉就可以了。
  初始写法：

class Solution():
    def maxSubarraySumCircular(self,A):
        # 单区间
        cur = ans = A[0]
        for num in A[1:]:
            cur = num + max(0,cur)
            ans = max(ans,cur)
        # 双区间
        all_sum = sum(A)
        # 找到中间最小值
        cur_min=ans_min = A[0]
        for num in A[1:]:
            cur_min = num + min(0,cur_min)
            ans_min = min(ans_min,cur_min)
        ans = max(ans,all_sum-ans_min)
        return ans 

错误案例：
忽略了全是负数的写法，这样会直接输出0，一个不选，也不好。

解决方案： 在ans = max(ans,all_sum-ans_min)前面增加一行：if ans_min==all_sum: return ans
这种剔除的需要在前期，写case，看这种要不要取。

解法2: 前缀和+ 单调队列

首先可以在定长数组上思考这个问题，循环数组A 的任意子段，一定是定长数组 A+A 的任意一个子段。

令B=A+A
假定 N = len(A), 考虑前缀和：
$$P_k=B[0]+B[1]+?+B[k?1]$$
考虑最大的 $P_j?P_i$, 其中$j?i\le N$.

固定j的最优结果$P_j?P_i$，我们希望有个$i$使得$P_i$ 尽可能小，并且满足 $j?N\le i<j$,对于第$j$个候选答案的最优$i$，我们可以使用有限队列实现它。

算法：
迭代$j$，每次计算第$j$个候选答案，我们维护一个queue保存可能的最优$i$ .
如果 $i_1<i_2$ 且 $P_{i_1}\ge P_{i_2}$ ，就不需要考虑$i_1$。

官方题解：

from collections import deque 

class Solution():
    def maxSubarraySumCircular(self,A):
        N = len(A)
        # compute p[j] = sum(B[:j]) for the fixed array A+A 
        P = [0]
        for _ in range(2):
            for x in A:
                P.append(P[-1] + x)
        
        # want largest p[j] - p[i] with 1 <= j-i <= N
        # for each j,want smallest p[i] with i >= j-N
        ans = A[0]
        res_dq = deque([0]) # 栈里是下标
        
        for j in range(1,len(P)): # 第一个是结果0
            # if the smallest i is too small, removie it 
            if res_dq[0] < j-N:
                res_dq.popleft()
            
            # the optimal i is deque[0], for candidate answer p[j]-p[i]
            ans = max(ans,P[j]-P[res_dq[0]])
            
            # remove and i1's with p[i_2] <= p[i_1]
            while res_dq and P[j] <= P[res_dq[-1]]:
                res_dq.pop()
            res_dq.append(j)
        return ans 

• 单调栈那边没有看懂。需要继续看。

300. 最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

用时：10:53 – 11:05
思路：维护一个单调栈，遍历元素，遇到比栈顶元素大的，直接append，遇到比栈顶小的，看栈里有没有合适的位置可以替换的，最后return 栈的长度。

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        stack = []
        for ele in nums:
            if not stack:
                stack.append(ele)
            else:
                if ele > stack[-1]:
                    stack.append(ele)
                # 比栈顶小才需要往前面替换
                # 找到第一个比ele小的元素，看它后面一个数字
                else:
                    # stack 长度为1，或者首个元素都比ele大
                    if stack[0]>ele:
                        stack[0] = ele 
                    else:
                        for j in range(len(stack)-2,-1,-1):
                            if stack[j]<ele:
                                if stack[j+1] > ele:
                                    stack[j+1] = ele 
                                break
                        
        return len(stack)

时间复杂度：这里的实现方式是o(n^2),如果后面对单调栈的搜索用二分查找，可以优化到 O(nlogn), 数据的长度为n，依次用数组的元素更新单调栈，更新单调栈需要用O(logn)的二分查找。
空间复杂度： O(n)

自己之前的解法：

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums)==1: return 1
        dp = [1 for n in nums]
        num_dict = {} # 记录数字最后一个index
        for i in range(len(nums)):
            # 往前找到第一个小于等于该值的index的位置 dp+1
            small_list = [dp[num_ind] for num,num_ind in num_dict.items() if num <nums[i]]
            if small_list:
                dp_v =  max(small_list)
                dp[i]= 1+ dp_v
            else:
                dp[i]=1
            num_dict[nums[i]] = i 
        return max(dp)