[数据结构与算法]二叉树非递归遍历基于栈和队列深度与广度遍历

二叉树 创建与递归遍历

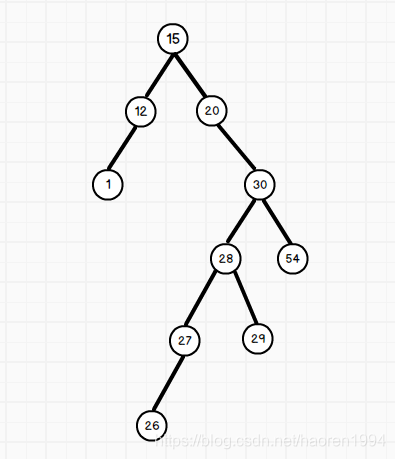
前序遍历

分析

栈的特点为先进和后出

前序遍历的特点为左 根 右

所以需要先将含有左子树的根进行压栈处理 待左子树处理完弹出根节点对右子树进行压栈处理

结合树进行分析

编码

public static void proOrder(MyTreeNode tree){

        if(tree == null) return;

        Stack<MyTreeNode> stack = new Stack<>();

        MyTreeNode tempNode = tree;

        while (tempNode != null || !stack.empty()){
			// 循环遍历左子树的值
            while (tempNode != null){
                stack.push(tempNode);
                tempNode = tempNode.getLeftNode();
            }
            MyTreeNode pop = stack.pop();
            System.out.println(pop.getNum());
			// 判断当前根是否存在右子树
            if(pop.getRightNode() != null){
                tempNode = pop.getRightNode();
            }

        }

    }

中序遍历

分析

前序遍历的特点为 根 左 右

所以需要先将根节点进行压栈 弹出 处理后再对左右子树进行压栈处理

结合树进行分析

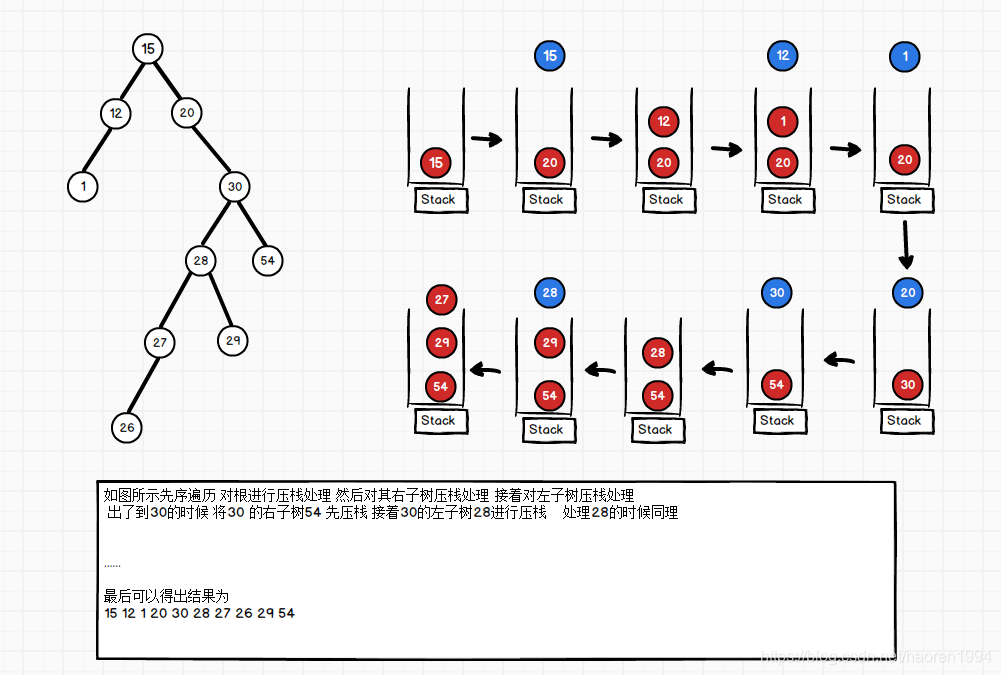
编码

    public static void inOrder(MyTreeNode tree){

        if(tree == null) return;

        Stack<MyTreeNode> stack = new Stack<>();
        stack.push(tree); // 根节点可以先压栈 进入循环体内就可以开始弹出元素

        while (!stack.empty()){
            MyTreeNode pop = stack.pop();
            System.out.println(pop.getNum());

            if(pop.getRightNode() != null){
                stack.push(pop.getRightNode());
            }

            if(pop.getLeftNode() != null){
                stack.push(pop.getLeftNode());
            }
        }

    }

后序遍历

分析

后序遍历的特点为 左 右 根

所以需要先将左节点压栈处理 然后是 右节点 最后是根

结合树进行分析

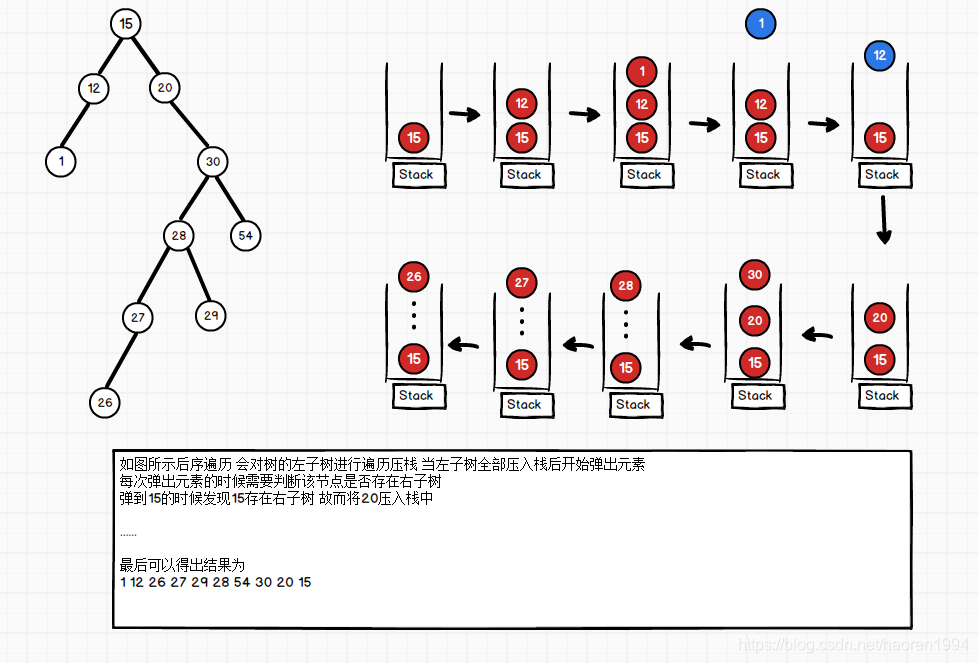
广度遍历、层级遍历

分析

广度遍历基于队列一级一级往下迭代遍历 遵循队列先进先出的特点

编码

  public static void testQueue(MyTreeNode tree) {
        if (tree == null) return;
        LinkedList<MyTreeNode> queue = new LinkedList<>();


        queue.offer(tree);
        while (!queue.isEmpty()) {

            MyTreeNode pop = queue.pop();
            System.out.println(pop.getNum());

            if(pop.getLeftNode()!=null){
                queue.offer(pop.getLeftNode());
            }

            if(pop.getRightNode()!=null){
                queue.offer(pop.getRightNode());
            }


        }
    }

https://blog.csdn.net/haoren1994/article/details/119277300

至此 ：二叉树的几种遍历已经全部完毕