[数据结构与算法]课堂作业（三）

2021.7.28

1、将向量下标为偶数的分量 ($x_2,x_4$, …) 累加, 写出相应表达式.
${\sum }_{imod2=0}^{\infty }$$x_i$
2、各出一道累加、累乘、积分表达式的习题, 并给出标准答案
R = { 1 , 1 , 2 , 2 } \mathbf{R}=\{1,1,2,2\} R={1,1,2,2}
${\sum }_{i=1}^4$${\mathbf{x}}_{\mathbf{i}}$=6
${\prod }_{i=1}^4{x}_i$=4
${\int }_1^3{x}^2\mathrm{d}x$=$\frac{1}{3}{x}^3{|}_1^3$=$\frac{28}{3}$
3、你使用过三重累加吗? 描述一下其应用.
没有使用过，也没查到相关资料，只查到了累加器
4、给一个常用的定积分, 将手算结果与程序结果对比
${\int }_1^3{x}^2\mathrm{d}x$

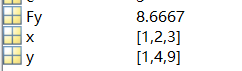
5、自己写一个小例子，来验证最小二乘法.

$\mathbf{X}=[{\mathbf{x}}_{\mathbf{i}\mathbf{j}}{]}_{3\times 2}$=$?\begin{array}{cc}1& 1\\ 1& 2\\ 1& 3\end{array}?$
$y_i$可以表示为：$\mathbf{Y}$=[11,20,32]${}^{\mathbf{T}}$
$\mathbf{W}=[a,b]$
求min$\Vert \mathbf{X}\mathbf{W}?\mathbf{Y}{\Vert }_2^2$
当$\mathbf{W}$=[10,1]时取得最小值；
所以，$y$=10$x$+1；$y_4$=41;

6、自己推导一遍Logistic回归, 并描述这个方法的特点 (不少于 5 条).

优点：

1. 实现简单，广泛的应用于工业问题上；

2. 容易使用和解释；

3. 便利的观测样本概率分数；

缺点：

1. 当特征空间很大时，逻辑回归的性能不是很好；

2. 容易欠拟合，一般准确度不太高；

3. 不能很好地处理大量多类特征或变量；