一、二叉树

一棵非空的二叉树由根结点 M 及左 L、右 R 子树这三个基本部分组成。

二叉树的遍历方式有 6 种：

MLR - LMR - LRM - MRL - RML - RLM

注意：前三种次序与后三种次序对称，故只讨论先左后右的前三种次序。

深度优先 DFS

MLR 前序遍历（Preorder Traversal ）
LMR 中序遍历（Inorder Traversal）
LRM 后序遍历（Postorder Traversal）

广度优先 BFS 层序遍历

在这里插入图片描述

1、TreeNode 类

# Definition for a binary tree node.
class TreeNode:
	#def __init__(self, val=0, left=None, right=None):
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

2、构建二叉树

def createBinaryTree(lst):
    if not lst:return None
    node = None
    data = lst.pop(0)
    if data:
        node = TreeNode(data)
        node.left = createBinaryTree(lst)
        node.right = createBinaryTree(lst)

    return node  

lst =  ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
root = createBinaryTree(lst)

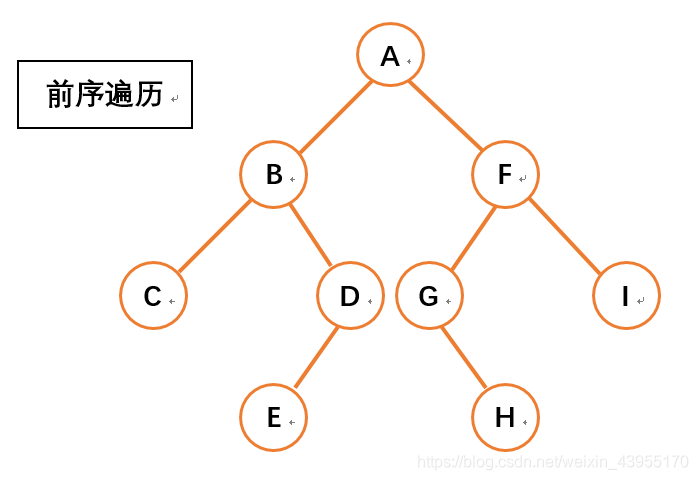
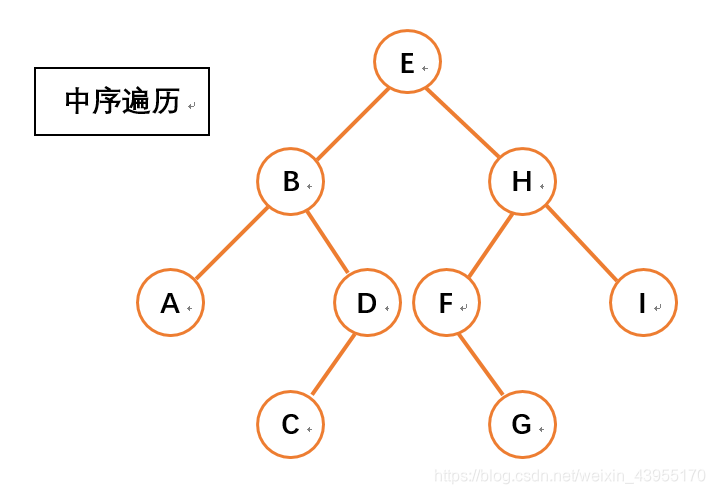
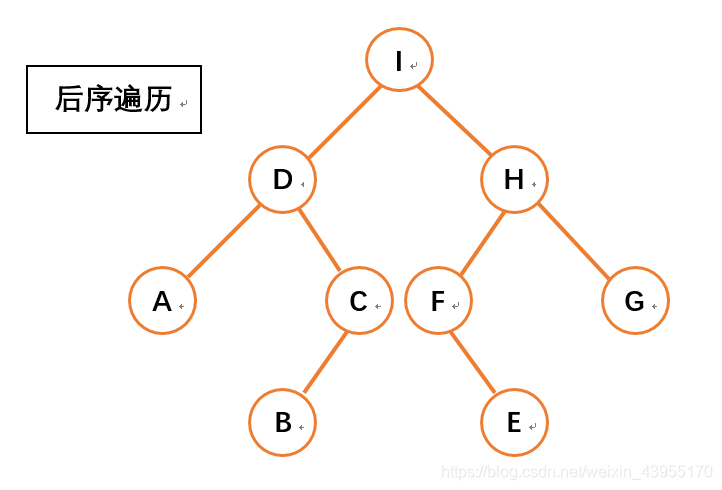
在这里插入图片描述

二、二叉树遍历

1、中序遍历

递归

def inorder(node):
    return inorder(node.left) + [node.val] + inorder(node.right) if node else []

循环

def inorderTraversal(node):
    res = []
    help = [node]
    cur = node.left
    
    while cur or help:
        while cur:
            help.append(cur)
            cur = cur.left
        
        cur = help.pop()
        res.append(cur.val)        
        cur = cur.right
        
#        if cur:
#             stack.append(cur)
#             cur = cur.left
#         else:
#             cur = stack.pop()
#             res.append(cur.val)
#             cur = cur.right

    return res

2、前序遍历和后序遍历

递归

def preorder(node):
    return [node.val] + preorder(node.left) + preorder(node.right) if node else [] 
    
def postorder(node):
    return postorder(node.left) + postorder(node.right) + [node.val] if node else []

循环

def postorderTraversal(root):
    if not root: return []
    stack = []
    res = []
    cur = root
    
    while cur or stack:
        while cur:
            stack.append(cur)             
            cur = cur.left if cur.left else cur.right 
            # 中序是先左入完，左出来才判断右，然后才入右。
            # 后序是先左入完，然后入右。
        
        #循环结束说明走到了叶子结点
        cur = stack.pop()  
        res.append(cur.val)
            # 中序是左先来，然后判断右。
            # 后序是直接判断栈顶，注意还没有出来。
        cur = stack[-1].right if stack and stack[-1].left == cur else None   # 栈顶没有出来就判断右，入右。
        
#         if cur:
#             res.append(cur.val)
#             stack.append(cur.right)
#             cur = cur.left
#         else:
#             cur = stack.pop()

    return res
    
  
def postorderTraversal(self, root): ## 后序遍历
    stack = []
    sol = []
    curr = root
    while stack or curr:
        if curr:
            sol.append(curr.val)
            stack.append(curr.left)
            curr = curr.right
        else:
            curr = stack.pop()
    return sol[::-1]

代码的主体部分基本就是.right和.left交换了顺序，且后序遍历在最后输出的时候进行了反向（因为要从中右左变为左右中）

3、层序遍历

层序遍历（广度优先）：从第一层结点开始，一层一层访问，同一层结点从左到右的顺序依次访问。

递归

递归函数需要有一个参数 level，该参数表示当前结点的层数。遍历的结果返回到一个二维列表 res = [[]] 中， res 中的每一个子列表保存了对应 index 层的从左到右的所有结点 value 值。

def levelOrder(root):
    """
    :type root: TreeNode
    :rtype: List[List[int]]
    """
    def helper(node, level):
        if not node: return
        else:
            res[level-1].append(node.val)
            if len(res) == level:  # 遍历到新层时，只有最左边的结点使得等式成立
                res.append([])
            helper(node.left, level+1)
            helper(node.right, level+1)
    res = [[]]
    helper(root, 1)
    return res[:-1]

PS：

Q：如果仍然按层遍历，但是每层从右往左遍历怎么办呢？
A：将上面的代码left和right互换即可
Q：如果仍然按层遍历，但是我要第一层从左往右，第二层从右往左，第三从左往右…这种 zigzag 遍历方式如何实现？
A：将 sol[level-1].append(node.val) 进行一个层数奇偶的判断，一个用append()，一个用 insert(0)

if level%2==1:
sol[level-1].append(node.val)
else:
sol[level-1].insert(0, node.val)

循环

这里的循环实现不能用栈了，得用队列 queue。因为每一层都需要从左往右打印，而每打印一个结点都会在队列中依次添加其左右两个子结点，每一层的顺序都是一样的，故必须采用先进先出的数据结构。

以下代码的打印结果为一个一维列表，没有采用二维列表的形式。

def levelOrder(root):
	if not root: return []
	res = []
 	cur = root
 	queue = [cur]
 	while queue:
     	cur = queue.pop(0)
     	res.append(cur.val)

     	cur.left and queue.append(cur.left)
		cur.right and queue.append(cur.right)

 return res