[数据结构与算法]【算法笔记】回文串

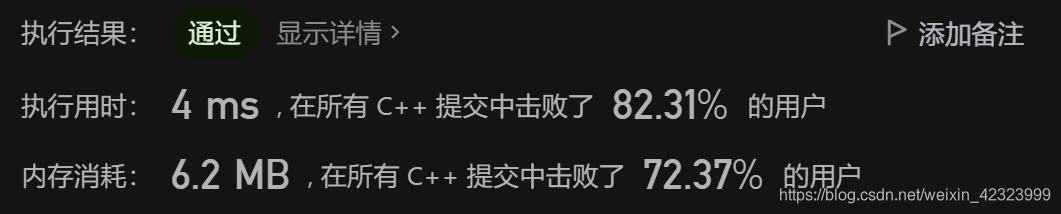
LC5 最长回文子串

1 枚举（超时）

stringPalindrome(string s) {
    int len = s.length();
    if(len < 2) return s;
    
    int maxlen = 1;
    int begin = 0;
    
    //枚举所有长度大于1的子串
    for(int i = 0; i < len - 1; ++i) {   //右边界
        for(int j = i + 1; j < len; ++j) {    //左边界
            if(j - i + 1 > maxlen && isValidPalindrome(s, i, j)) {
                maxlen = j - i + 1;
                begin = i;
            }
        }
    }
    return s.substr(begin, maxlen);
}

bool isValidPalindrome(string s, int left, int right) {
    while(left < right) {
        if(s[left] != s[right]) return false;
        left++;
        right++;
    }
    return true;
}

2 动态规划

状态定义：dp[i][j]：s[i,j]是否为回文子串

string longestPalindrome(string s) {
    int n = s.length();
    if(n < 2) return s;

    int maxlen = 1;
    int begin = 0;
    //dp[i][j]表示s[i,j]是否为回文子串
    vector<vector<int>> dp(n, vector<int>(n));
    //bc1：初始化，所有长度为1的子串都是回文串
    for(int i = 0; i < n; ++i) {
        dp[i][i] = true;
    }
    //递推开始：从长度较短的字符串向长度较长的字符串进行转移
    //先枚举子串长度
    for(int len = 2; len <= n; ++len) {
        //枚举左边界
        for(int i = 0; i < n; ++i) {
            //由len和i确定右边界   j - i + 1 = len --->  j = i + len - 1;
            int j = i + len - 1;
            if(j >= n) break; //右边界越界

            if(s[i] != s[j]) {
                dp[i][j] = false;
            }
            else {
                if(len <= 3) {    //bc2：长度为2的子串，只要它的字母相同，它就是一个回文串
                    dp[i][j] = true;
                }
                else {
                    //状态转移方程：
                    //只有s[i+1:j-1]是回文串，并且s的第i和第j个字母相同时，s[i:j]才会是回文串
                    dp[i][j] = dp[i + 1][j - 1];
                }
            }
            //只要 dp[i][j] = true,  就表示s[i,j]是回文，此时记录回文长度和起始位置
            if(dp[i][j] && j - i + 1 > maxlen) {
                maxlen = j - i + 1;
                begin = i;
            }
        }
    }
    return s.substr(begin, maxlen);
}

3 中心扩展法

string longestPalindrome(string s) {
    int n = s.length();
    int left = 0, right = 0;
    //遍历每个位置，作为中心点
    for(int i = 0; i < n; ++i) {
        //奇数回文子串长度
        int oddlen = expandCenter(s, i, i);
        //偶数回文子串长度
        int evenlen = expandCenter(s, i, i + 1);
        int maxlen = max(oddlen, evenlen);
        //计算回文子串的左右边界
        if(maxlen > right - left + 1) {
            left = i - (maxlen - 1) / 2;
            right = i + maxlen / 2;
        }
    }
    return s.substr(left, right - left + 1);
}

int expandCenter(string s, int left, int right) {
    while(left >= 0 && right < s.length() && s[left] == s[right]) {
        left--;
        right++;
    }
    //回文串的长度(left, right)  right - left + 1 - 2  
    return right - left - 1;
}

LC647 回文子串

给定字符串，计算这个字符串有多少个回文子串？

1 枚举

int countSubstrings(string s) {
    int n = s.length();
    int cnt = n;
    for(int i = 0; i < n; ++i) {
        //从长度为2的回文子串开始枚举
        for(int j = i + 1; j < n; ++j) {
            if(isValidSubstring(s, i, j)) {
                cnt += 1;
            }
        }
    }
    return cnt;
}

bool isValidSubstring(string s, int left, int right) {
    while(left < right) {
        if(s[left] != s[right]) return false;
        left++;
        right--;
    }
    return true;
}

2 动态规划

在上一道题的基础上修改：

int countSubstrings(string s) {
    int n = s.length();
    if(n < 2) return n;
    int cnt = n;
    vector<vector<bool>> dp(n, vector<bool>(n));
    for(int i = 0; i < n; ++i) {
        dp[i][i] = true;
    }
    //回文子串长度
    for(int len = 2; len <= n; ++len) {
        //右边界
        for(int i = 0; i < n ; ++i) {
            int j = i + len - 1;
            if(j >= n) break;
            if(s[i] != s[j]) dp[i][j] = false;
            else {
                if(len <= 3) {
                    dp[i][j] = true;
                }
                else {
                    dp[i][j] = dp[i + 1][j - 1];
                }
            }
            if(dp[i][j]) cnt += 1;
        }
    }
    return cnt;
}

参考评论区的一种解法：

dp[j]表示从j位置到当前遍历到的字符位置i是否为回文字符串

int countSubstrings(string s) {
    int n = s.length();
    vector<int> dp(n);
    int res = 0;
    for(int i = 0; i < n; ++i) {
        dp[i] = 1;
        res++;
        for(int j = 0; j < i; ++j) {
            if(s[j] == s[i] && dp[j + 1] == 1) {
                dp[j] = 1;
                res++;
            }
            else {
                dp[j] = 0;
            }
        }
    }
    return res;
}

3 中心扩展法

int res = 0;
int countSubstrings(string s) {
    int n = s.length();
    if(n < 2) return n;
    for(int i = 0; i < n; ++i) {
        expandCenter(s, i, i);
        expandCenter(s, i, i + 1);
    }
    return res;
}

void expandCenter(string& s, int left, int right) {
    while(left >= 0 && right < s.size() && s[left] == s[right]) {
        res++;
        left--;
        right++;
    }
}