[数据结构与算法]二.链表——习题解

前置知识

typedef struct Lnode{      //单链表的定义
	int data;
	Lnode *next;
}*Linklist,Lnode;

int length(Linklist L) {   //求长度的函数
	int s = 0;
	while (L->next != NULL) {
		s++;
		L = L->next;
	}
	return s;
}

带头节点的链表，一般传指针Linklist L，在执行的时候，会将指针备份，并将备份的指针进行运算（也就是函数体内的L），备份的L可以改变链表，但是不会改变原指针L的内容。所以在函数内用L进行运算，实际上L仍然指向头结点。
无头节点的链表，按需要传引用Linklist &L，引用是变量的别名，就相当于我们直接在该指针上进行操作，可以改变L的内容。

Ⅰ 结点的查找、删除

一.递归——&L , Q(L->next)

为了方便进行遍历运算，我们直接默认传入的是无头结点的单链表，若要对有头结点的链表进行操作，可直接传入 Q1(L->next)。（实际上通用）

1.逆序输出

Q3 带头结点的单链表进行逆序输出：

void Q3(Linklist L){
	if(L->next!=NULL)      //压栈
		Q3(L->next);
	if(L!=NULL)          //从栈顶开始依次输出
		cout<<L->data<<end="  ";
}
void withhead(Linklist L){
	Q3(L->next);
}

2.删除结点

Q1 对于无头结点的链表，递归删除所有值为x的结点。

/*Q1 不带头结点，递归删除所有值为x的结点*/
void Q1(Linklist& L, int x) {  //L为引用,next域传递，需要在原链表上进行，不能传L的复制值，只能传L的引用
	if (L == NULL)
		return;
	if (L->data == x) {       //1.为什么这里没有断链？？
		Lnode* p = L;
		L = L->next;         //3.假设第二次调用此处，上一次指针为L1，传入(L1->next) 此处可以理解为(L1->next)=(L1->next)->next，跳过了当前的
		delete(p);
		Q1(L, x);
	}
	else
		Q1(L->next, x);   //2.因为这里传的是L的next域，并不是一个普通指针（正因为递归的是L->next,实际上L不会到链尾）
}

二.删除结点

1.一般删除——pre,p

Q2 带头结点，删除所有值为x的结点。
Q7 无序单链表中删除介于min,max之间的值的结点。

以Q2为例，其他大同小异，均是找到符合的删除即可。对于删除一个元素，我们需要找到其前驱元素，一个指针或者双指针均可以完成。双指针直观明了，建议双指针。
单指针：用 L->next 遍历链表，L即为前驱。

void Q(Linklist L,int x){
	while(L->next!=NULL){
		if(L->next->data==x){
			Lnode *p=L->next;
			L->next=p->next;  //指针传递
			delete(p);
		}
		else
			L=L->next;
	}
}

双指针 ：pre=L 表前驱；p=L->next ，表示删除的那个结点

void Q7(Linklist L, int min, int max) {         
	Lnode* pre = L, * p = L->next;             //带头节点的单链表的删除，可以双指针运行
	while (p != NULL) {
		if (p->data > min && p->data < max) {
			pre->next = p->next;   //此处删除不需要新开指针！！
			delete(p);
			p = pre->next;
		}
		else{
			pre = p;
			p = p->next;
		}
	}
}

2.去重——数组

Q12 递增有序单链表删重复元素
Q23 保存绝对值相同第一个结点，删除其后的所有相同结点，结点值的绝对值<=n(时间复杂度尽可能高效)

Q23 用数组记录要删去的结点。

void Q23_offical(Linklist L,int n) {     //开辟 n+1大小数组，以空间换时间 空间O(n),时间O(m)
	int* a = new int[n + 1];
	for (int i = 0; i < n + 1; i++) 
		a[i] = 0;            //初始化为0
	Lnode* pre = L, * p = L->next;
	while (p != NULL) {
		if (a[abs(p->data)] == 0) {
			a[abs(p->data)]++;
			pre = p;
			p = p->next;
		}
		else {
			pre->next = p->next;
			delete(p);
			p = pre->next;
		}
	}
}

基本操作——删除结点：

pre->next = p->next;  
delete(p);
p = pre->next;

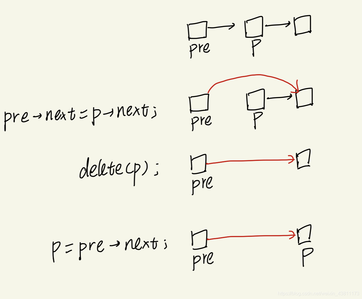
三.找最小值结点——4指针，2指针

1.最小值——minpre,minp

Q4 带头结点的单链表中删除最小值(唯一)

删除最小值我们可以用两个指针（pre,p），或者是四个指针(pre,p,minpre,minp)。

四个指针：pre、p、minpre、minp。
其中pre,p为工作指针，p遍历列表，pre为其前驱。minp保存最小值结点，minpre保存其前驱。

void Q4_offical(Linklist L) {
	Lnode* pre = L, * p = L->next;       //pre=L表前驱，p=L->next表当前
	Lnode* minpre = pre, * minp = p;
	while (p != NULL) {
		if (p->data < minp->data) {
			minp = p;
			minpre = pre;
		}
		pre = p;
		p = p->next;
	}
	minpre->next = minp->next;
	delete(minp);
}

双指针：pre保存最小值结点的前驱，p工作指针遍历链表

Lnode* pre = head, * p = head ->next;
while (p->next != NULL) {
	if (p->next->data < pre->next->data)
		pre = p;        //pre保存最小值结点的前驱
	p = p->next;
}

2.递增排序——while(L->next){…}

Q6 单链表递增排序

Linklist Q6(Linklist L) {		//选择排序，为O(n^2)
	Linklist L1 = new Lnode;  //每次选出最小的进入新链表,头插法
	L1->next = NULL;
	while(L->next!=NULL){	//找出所有最小值
		Lnode* pre = L, * p = L->next;
		Lnode* minpre=pre, * minp=p;
		while (p != NULL) {
			if (p->data < minp->data) {
				minp = p;
				minpre = pre;
			}
			pre = p;
			p = p->next;
		}
		minpre->next = minp->next;
		minp->next = L1->next;
		L1->next = minp;
	}
	return L1;
}

3.递增输出

Q9 递增输出结点值并释放结点，不可用数组
Q19 带头结点的单链表，值均为正整数，反复输出最小值并删除，最后删除头结点

void Q19(Linklist L) {
	while (L->next != NULL) {
		Lnode* pre = L, * p = L->next;
		Lnode* minpre = pre, * minp = p;    //老老实实用四个指针方便，用双指针还要考虑首元结点
		while (p != NULL) {
			if (p->data < minp->data) {
				minp = p;
				minpre = pre;
			}
			pre = p;
			p = p->next;
		}
		cout << minp->data << "  ";
		minpre->next = minp->next;
		delete(minp); 
	}
	delete(L);
}

基本操作——找最小值：

Lnode* pre = L, * p = L->next;
Lnode* minpre=pre, * minp=p;
while (p != NULL) {
	if (p->data < minp->data) {
		minp = p;
		minpre = pre;
	}
	pre = p;
	p = p->next;
}

四.找倒数第k个位置——双指针

Q21 带头结点的单链表，查找倒数第k个位置上的结点，成功输出data值并返回1，失败返回0(时间复杂度尽可能高效)

再遍历一遍的情况下，找到第k个位置。我们只需两个指针即可，让p和L始终相差 k-1 个结点。
我的：

bool Q21(Linklist L,int k) {
	Lnode* p = L->next;   //让p与L之间始终差k-1个结点
	if (k <= 0)     //若k不是正整数
		return 0;
	for (int i = 0; i < k; i++) {
		L = L->next;
		if (L == NULL)    //要是k超出了链长
			return 0;
	}   
	while (L->next != NULL) {
		L = L->next;
		p = p->next;
	}
	cout << p->data << "  ";
	return 1;
}

标准解析：

bool Q21(Linklist L, int k) {
	Lnode* p = L->next, * q = L->next;
	int count = 0;
	while (q != NULL) {
		if (count < k)      //这一段够巧的
			count++;
		else
			q = q->next;
		p = p->next;
	}
	if (count != k)
		return 0;
	else
		cout << q->data << "  ";
	return 1;
}

标答果然牛逼 精简巧妙

五.公共结点——求差值，同长跑

Q8 给定两个单链表，找出所有公共结点
Q22 找到两个单链表的第一个公共结点

由于单链表只有一个 next 域，所以第一个公共结点后都应该是公共节点。

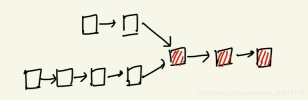
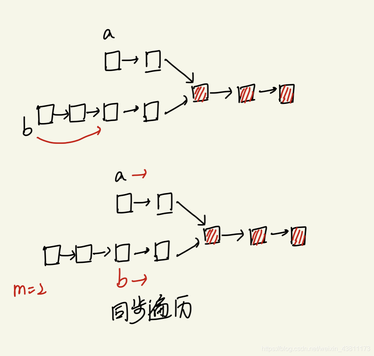
算法思想：
先求得两链表A,B的表长，la,lb，求得差值 m，让长的那个表先遍历m个结点，然后再与短的链表一起遍历，直到找到第一个 data值相同的结点。

Linklist Q22(Linklist A,Linklist B){
	int l1 = length(A), l2 = length(B);
	if (l1 < l2)
		Q22(B, A);       //保证l1>=l2
	int m = l1 - l2;     //得到差值m
	while(m--){        
		A = A->next;	 //长的先走m个结点
	}
	while (A->next != NULL) {
		if (A->data == B->data)
			return A;
		else {
			A = A->next;
			B = B->next;
		}
	}
	return NULL; //若没有
}

保证l1>=l2：

if(l2>l1)
	Q(l2,l1);

六.公共元素——双指针比较，小的后移

均是指递增单链表的公共元素。

Q14 A,B是带头递增有序单链表，利用A，B的公共元素生成表C，且不破坏A，B的结点
Q15 求递增集合A,B的交集，并存放在A中

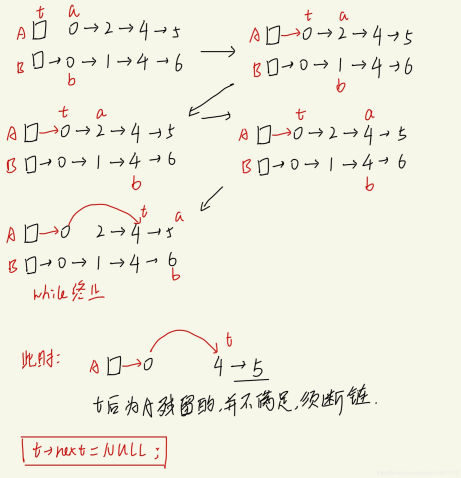
求公共元素和求公共结点有点相似，但是公共结点只要找到第一个即可，而公共元素有多个，需要找到每一个。
由于都是递增的链表，我们可以用两个指针分别在两个链表上进行遍历，每次比较，若相同则取出结点放入新链表，然后指针都后移；若不同，较小的后移，继续比较。直到其中一个链表走到链尾结束。
因为是要生成链表——记得尾部置空

Linklist Q14(Linklist A, Linklist B) {
	Linklist C = new Lnode;
	Lnode* a = A->next, * b = B->next, * c = C; //a,b是工作指针,
	Lnode* p;
	while (a != NULL && b != NULL) {
		if (a->data < b->data)       //小的后移
			a = a->next;
		else if (a->data > b->data)
			b = b->next;
		else{
			p = new Lnode;
			p->data = a->data;
			c->next = p;   //尾插法
			c = p;
			a = a->next;
			b = b->next;
		}
	}
	c->next = NULL;     //尾部置空 （链的分割、拼接都要注意尾部置空）
	return C;
}

Q15：未删除其他结点（写了懒得放）。

void Q15(Linklist A, Linklist B) {
	Linklist a = A->next, b = B->next;  //工作指针,进行比较
	A->next = NULL;   				//将A的头结点断开
	while (a!=NULL && b!=NULL) {
		if (a->data < b->data) 
			a = a->next;
		else if (a->data > b->data) 
			b = b->next;
		else {
			A->next = a;
			A = a;
			a = a->next;
			b = b->next;
		}
	}
	A->next = NULL;   //尾部置空
}

Ⅱ 链表的逆置、拆分、合并

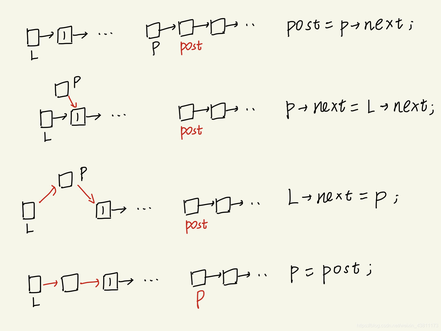
一.逆置 = 头插 (post,p)

Q5 将带头节点的单链表就地逆置

注：头插法的时候，需额外的指针 post，保存 p->next，使得遍历进行下去。

void Q5(Linklist L) {  
	Lnode* p = L->next;  //工作指针
	Lnode* post;            //保存下一个
	L->next = NULL;   //把头结点取下来
	while (p != NULL) {
		post = p->next;         //保留下一个
		p->next = L->next;  
		L->next = p;
		p = post;
	}
}

二.拆分奇偶结点——头/尾插

注：生成新链表——尾插：尾部断链 p=NULL

Q10 将带头节点的链表分成两个带头节点的链表，一个保存所有奇数结点，一个保存所有偶数结点
Q11 同10拆分奇偶结点，基的顺序排(尾插)，偶的逆序排(头插)

注：尾插法→尾部断链，对于拆分的题目，一般是将相应的结点连接到新链表中，若结点的next域没有断开(还是连接在原链表中)，那么最后一定要对新生成的链表进行尾部断链
头插法→不需要断链
对于奇偶结点的选取，可以用计数器，或者不用，一次处理两个结点即可。

1.使用计数器，两个都是尾插(顺序)

Linklist Q11(Linklist A) {
	Linklist B = new Lnode;
	B->next = NULL;
	Lnode* a = A, * b = B;
	Lnode* p = A->next;  //工作指针
	int i = 0;			//计数器
	while (p != NULL) {
		i++;
		if (i % 2 != 0) {   //奇数，尾插，顺序 
			a->next = p;
			a = p; 
			p = p->next;
		}
		else {            //偶数，头插，逆序
			Lnode* temp = p->next;
			p->next = b->next;
			b->next = p;
			p = temp;
		}
		
	}
	a->next = NULL;    //防止A全部处理完后接着B，所以需要断链,害！！！！！！
	b->next = NULL;
	return B;
}

2.不用计数器，一个尾插(顺序),一个头插(逆序)

Linklist Q11_offical(Linklist A) {   //不需要计数器，先尾插再头插
	Linklist B = new Lnode;
	B->next = NULL;
	Lnode* a = A;      //a为A的尾指针
	Lnode* p = A->next, * post;
	while (p != NULL) {
		a->next = p;         //A尾插
		a = p;  
		p = p->next;       //工作指针后移
		if (p != NULL){  
			post = p->next;  
			p->next = B->next;      //B头插，B不变
			B->next = p;
			p = post;
		}
	}
	a->next = NULL;  //头插一开始尾部就是NULL,不需要置空，尾插需要
	return B;
}

三.合并链表——头/尾插

Q13 将两个递增链表合并成一个递减列表(头插)，相对次序不变

void Q13(Linklist L1, Linklist L2) {
	Lnode* p1 = L1->next, * p2 = L2->next;  //两个工作指针
	Lnode* post;  //保存后一个结点
	L1->next = NULL;  //断开L1的头，让L1的头结点做新头
	while (p1 != NULL && p2 != NULL) {
		if (p1->data < p2->data) {
			post = p1->next;
			p1->next = L1->next;
			L1->next = p1;
			p1 = post;
		}
		else {
			post = p2->next;
			p2->next = L1->next;
			L1->next = p2;
			p2 = post;
		}
	}
	if (p1)
		p2 = p1;      //如果p1还有，统一处理
	while (p2 != NULL) {  //若p2还有
		post = p2->next;
		p2->next = L1->next;
		L1->next = p2;
		p2 = post;
	}
}

Ⅲ 杂项

一.连续子序列——1个外指针，2个内指针

Q16 两个链表A,B，判断B序列是否为A序列的连续子序列

该题为字符串模式匹配的链式表示形式。可继续优化。
外指针从A头扫到尾，对于外指针的每个结点，两个内指针分别进行比较。不匹配就重置。

bool Q16_offical(Linklist A, Linklist B) {   //答案是无头结点的，我喜欢有头结点的
	Lnode* a = A->next, * b = B->next;    //两个内指针，进行匹配
	Lnode* p = A->next;            //A的外指针，方便重置
	while (a != NULL && b != NULL) {
		if (a->data == b->data) {
			a = a->next;
			b = b->next;
		}
		else {
			p = p->next;     //A上外指针p后移,内指针a也重置为p
			a = p;
			b = B->next; //重置b
		}
	}
	if (b == NULL)     //匹配的判断是b==NULL
		return 1;
	else
		return 0;
}

自己最开始写的：

bool Q16(Linklist A, Linklist B) {    //暴力解法，对A的每个结点，去尝试B
	int lb = length(B);
	Lnode* a = A->next;   //外指针
	while (a != NULL) {
		Lnode* ta = a, * tb = B->next;  //俩内指针
		int i = 0;
		while (tb != NULL && ta != NULL) {
			if (ta->data == tb->data) {
				i++;
				ta = ta->next;
				tb = tb->next;
			}
			else
				break;
		}
		if (i == lb)
			return true;
		else
			a = a->next;
	}
	return false;
}

看了下，我这个用计数器来判断的，并且重置是直接Lnode重新定义，yysy确实不行，贴上来鞭笞移下。

二.双链表

双链表：

typedef struct Dnode {
	int data;
	Dnode* prior, * next;
}*Dlinklist,Dnode;

1.判断是否对称——（a != b && b->next != a）

Q17 判断带头结点的循环双链表是否对称

因为有两种对称，1221和12121，对于第二种，终止条件是 a!=b ,对于第一种双指针若一直比较会交错而过，此时的终止条件是 b->next !=a。
a b → b a ,所以判断条件是 b->next !=a ！

bool Q17_offical(Dlinklist L) {
	Dnode* a = L->next, * b = L->prior;
	while (a != b && b->next != a) {      //此处为b->next!=a ,刚好避免了1221的情况
		if (a->data == b->data) {
			a = a->next;
			b = b->prior;
		}
		else
			return 0;
	}
	return 1;
}

2.按访问频度freq排列

Q20 给结点增加一个频度freq，初始值为0，每一次locate(L,x)，freq＋1，然后将所有结点按照freq递减排列，相同频度的最近一次访问的排前面

typedef struct Q20list {
	int data,freq=0;
	Q20list* prior, * next;

}Q20list,* Q20link;

Q20link Q20(Q20link L,int x) {    //按值访问
	Q20list* pre = L, * p = L->next;
	//找值
	while (p != NULL) {
		if (p->data == x) {
			p->freq++;
			break;
		}
		pre = p;        //pre保存该节点前驱，p保存该节点
		p = p->next;
	}
	if (p == NULL) //要是没有，直接返回L
		return L;
	//排序
	Q20list* r1=L,* r2=L->next;     
	while (r2 != NULL) {
		if (r2->freq <= p->freq) {  //找到第一个freq小于等于p的
			Q20list* temp = p->next;
			p->next = r2;
			p->prior = r1;
			pre->next = temp;
			temp->prior = pre;
			r1->next = p;
			break;
		}
		r1 = r2;
		r2 = r2->next;
	}
	return L;
}

三.是否有 环

Q24 判断一个链表是否有环，若有找到环的入口点并返回，否则返回NULL

用两个指针，一快一慢，fast每次走两步，slow每次走一步，若有环，fast必然先进环且与slow在环中某点相遇。
求环的入口：
出发点与入口距离：a，入口距离相遇点：x，环长：r
则2(a+x)=a+n*r+x
左边是slow跑的距离的两倍，右边是fast跑的距离，因为fast是slow速度的两倍，所以相等。

Linklist Q24(Linklist L) {
	Lnode* fast = L, * slow = L;    //快慢指针
	while (fast != NULL && fast->next != NULL) {  //此处书上是while(slow!=NULL && fast->next!=NULL) ，不妥
		slow = slow->next;					      //若只有一个首元结点，第二次判断是fast已经是NULL了
		fast = fast->next->next;
		if (slow == fast)
			break;
	}
	if (fast == NULL || fast->next == NULL)
		return NULL;
	Lnode* p1 = L, * p2 = slow;
	while (p1 != p2) {
		p1 = p1->next;
		p2 = p2->next;
	}
	return p1;
}

日撸代码500行，小丁要做苦行僧
两天码了1000多行，人麻了，链表这玩意题目咋这么多啊，写的我脑壳昏，麻了
王道咋不出个软件，把测试案例都给整好啊，一个个写真tm麻烦，有些边界条件也没跑......
答案还有错的，可能是假书吧...