一、线性回归
1、简介
1.1 应用场景
- 房价预测
- 销售额度预测
- 货款额度预测
1.2 定义
- 定义:利用回归方程对一个或多个自变量(特征)和因变量(目标值)之间关系进行建模;
- 特点:一个自变量为变量回归,多个自变量为多元回归;

1.3 线性回归的特征与目标的关系分析
具有线性和非线性关系。
1.3.1 线性关系
单变量线性关系
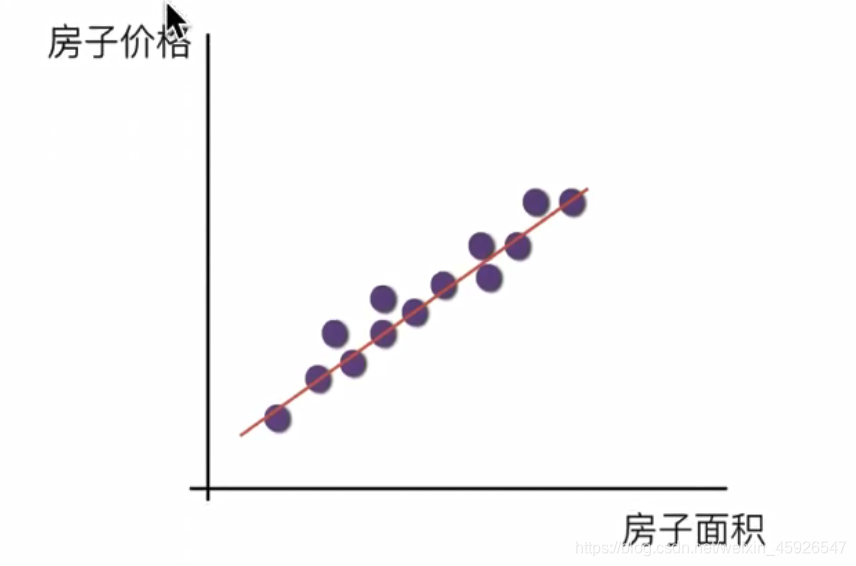
多变量线性关系
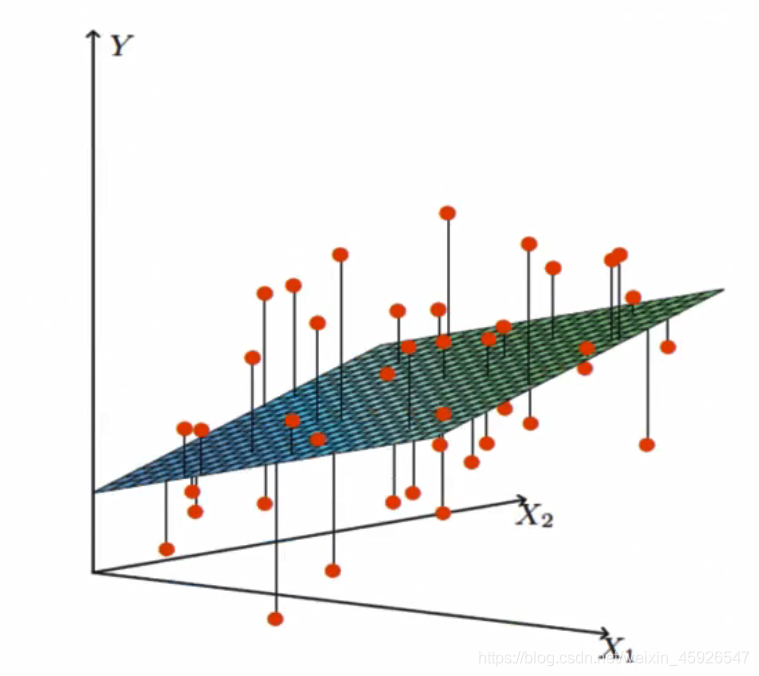
1.3.2 非线性关系

2、线性回归API
2.1 API
sklearn.linear_model.LinearRegression()
LinearReggression.coef_:回归系数;
2.2 步骤分析
- 获取数据集
- 数据基本处理
- 特征工程
- 机器学习
- 模型评估
2.3 案例
# -*- coding: utf-8 -*-
""" @Time : 2021/7/31 16:28
@Author : XXX
@Site :
@File : linearRegressionDemo.py
@Software: PyCharm
"""
from sklearn.linear_model import LinearRegression
x = [
[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80]
]
y = [84.2, 80.6, 80.1, 90, 83.2,87.6,79.4]
estimator = LinearRegression()
estimator.fit(x,y)
_coef = estimator.coef_
print(_coef)
3、求导


4、损失和优化
4.1 损失函数
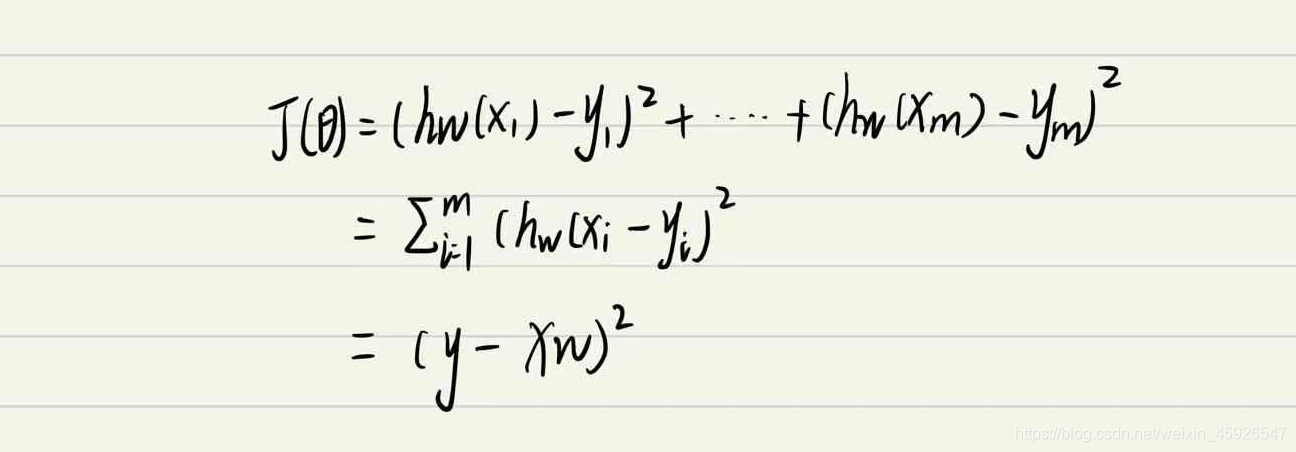
- yi为第i个训练样本的真实值;
- h(xi)为第i个训练样本特征值组合预测函数;
- 又称最小二乘法
- y为真实矩阵,X是特征矩阵,w是权重矩阵
4.2 优化算法
目的:找到最小损失对应的w值;
4.2.1 正规方程
公式:
w = (X^T * X)^-1 * X^T * y
- X为特征值矩阵,y为目标值矩阵;
- 缺点:当特征过多过复杂时,求解速度太慢且得不到结果。只适合样本和特征较少的。
推导
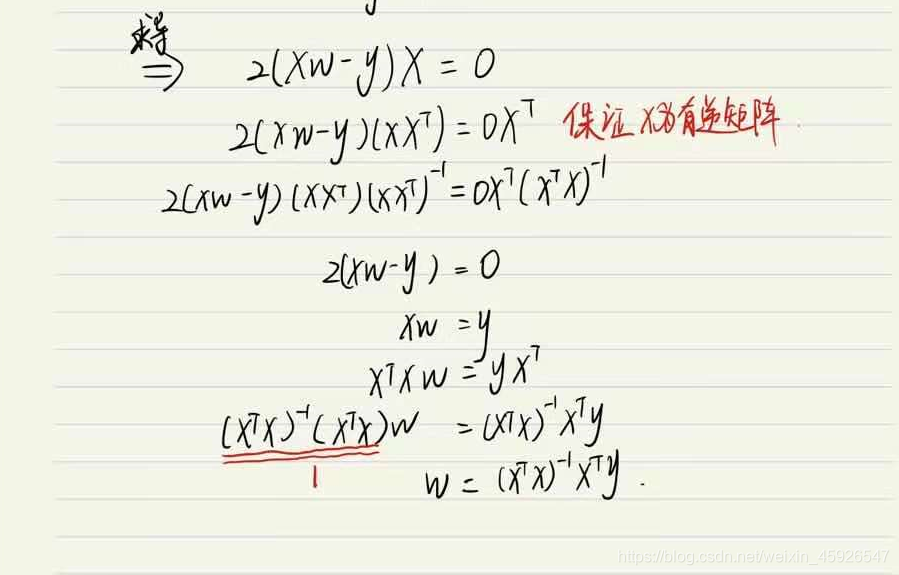
4.2.2 梯度下降
原理:寻找最陡峭的位置,向高度向下的地方走。

概念
- 在单变量函数中,梯度就是函数的微分,代表函数在某个给定的切线的斜率;
- 在多变量函数值,梯度是一个向量,梯度的方向是给定点上升最快的方向,后沿着梯度方向走。

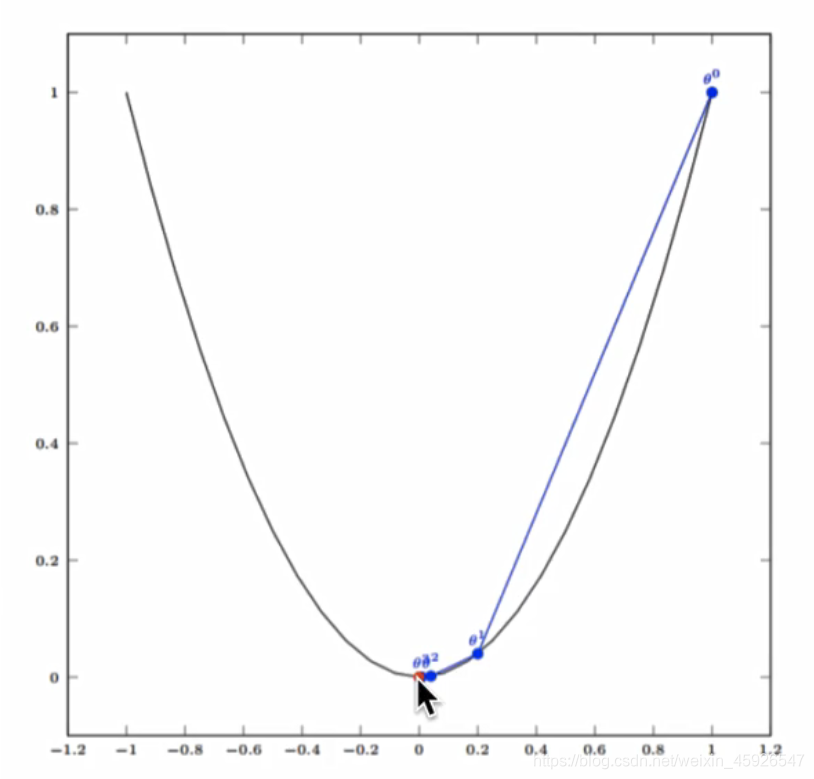
公式:
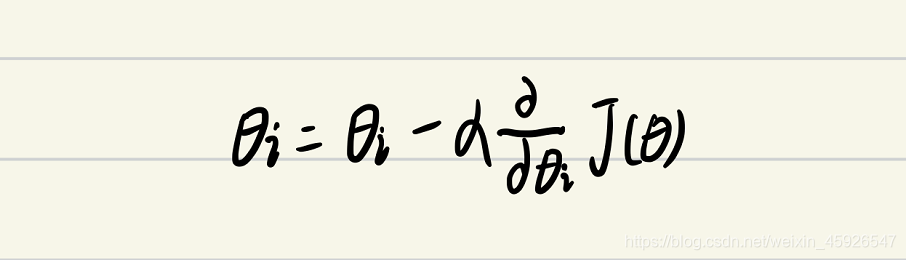
α:学习率或步长,控制每一步的距离。保证不大不小,太大易错过最低点,太小速度太慢;梯度加个负号:梯度方向是上升最快的地方,我们要向下走,反向的所以要加个负号;
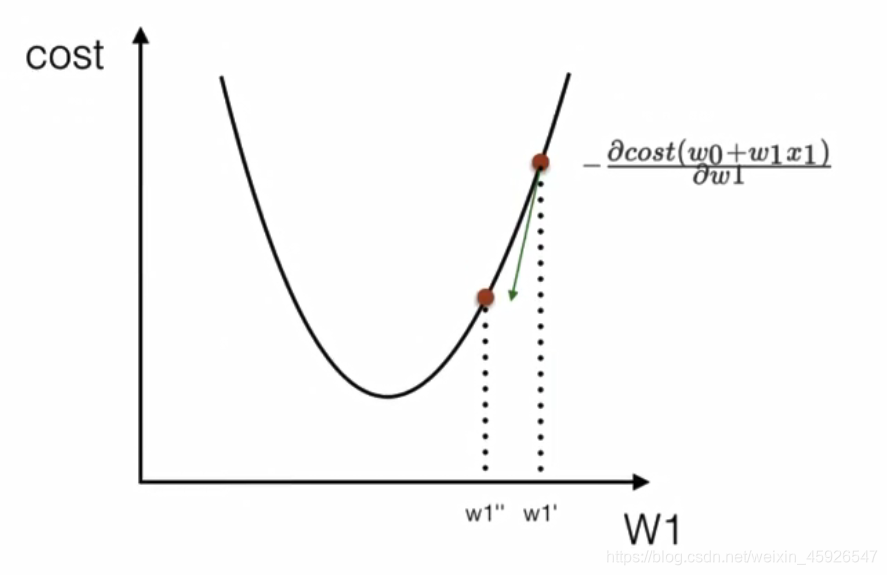
4.2.3 梯度下降对比正规方程
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可用 | 需计算方程,时间复杂度O(n3) |
4.2.4 API
小规模数据:
LinearRegression:不能解决拟合问题,岭回归;
大数据规模:
SGDRegressor
5、梯度下降
5.1 全梯度下降(FG)
计算所有样本的误差平均值,作为目标函数。
5.2 随机梯度下降(SG)
每次只选择一个样本进行计算。
5.3 小批量梯度下降算法(mini-bantch)
选择一部分数据。
5.4 随机平均梯度下降算法(SAG)
会给每一个样本都维持一个平均值。
5.5 算法比较
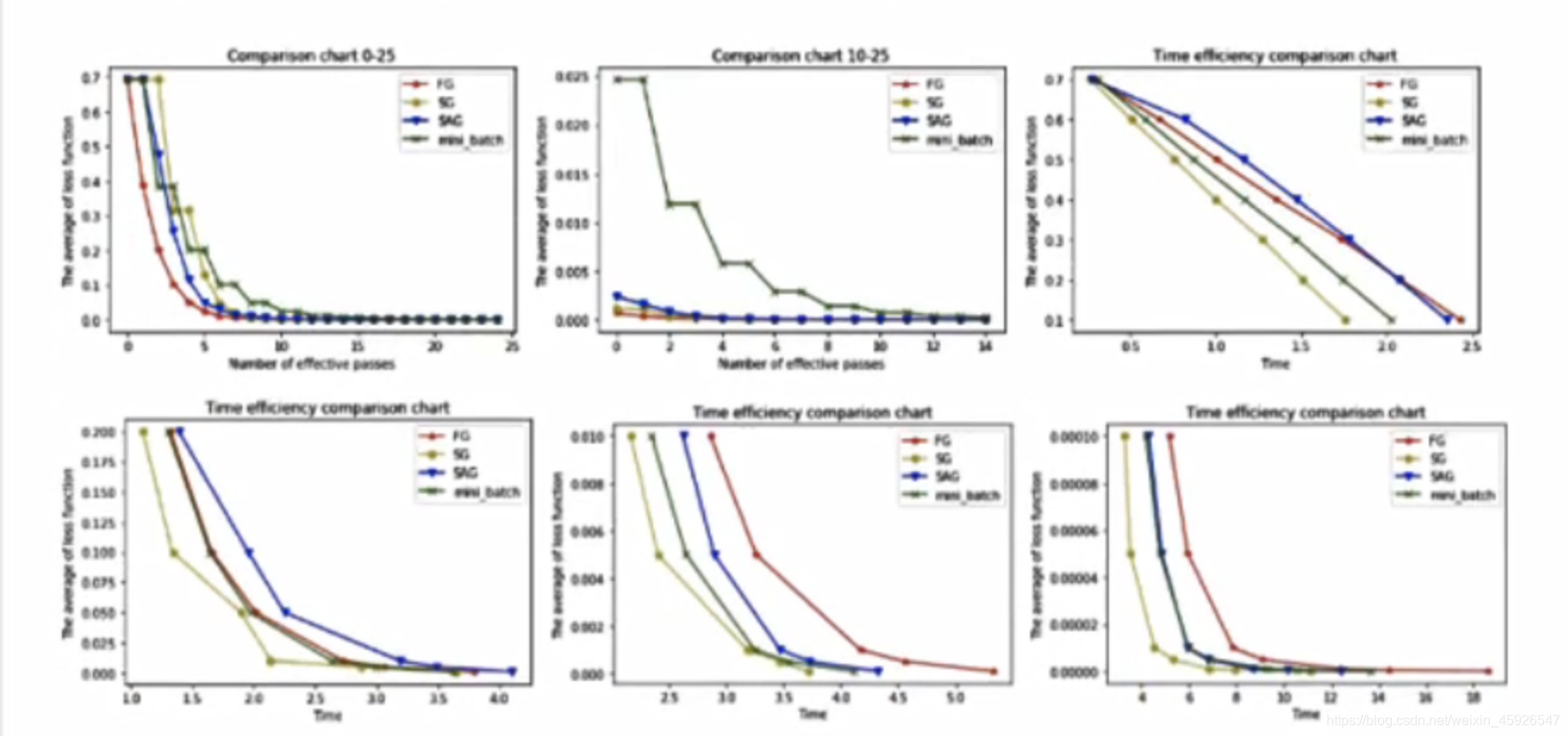
- FG由于它每轮更新都要使用全体数据集,故花费时间成本最多,内存存储最大;
- SAG优化速度较慢
5.6 梯度下降优化算法
5.6.1 动量法
- 是SAG的姐妹版;
- SAG是对过去K次的梯度求平均值;
- SAG是对过去所有的梯度求加权平均。
5.6.2 Nesterov加速梯度下降法
- 类似于一个
智能球,在重新遇到斜率上升时候,能够知道减速。
5.6.3 Adagrad
- 让
学习率使用参数;- 对于出现
次数较少的特征,我们对其采用更大的学习率,对于出现次数较多的特征,我们对其采用较小的学习率。
5.6.4 Adadelta
- Adadelta是Adagrad的一 种扩展算法,以
处理Adagrad学习速率单调递减的问题。
5.6.5 RMSProp
- 其结合了梯度
平方的指数移动平均数来调节学习率的变化。- 能够在不稳定(Non-Stationary) 的目标函数情况下进行很好地收敛。
5.6.6 Adam
- 结合AdaGrad和RMSProp两种优化算法的优点。
- 是一种
自适应的学习率算法
6、线性回归API
6.1 sklearn.linear. _model.LinearRegression(fit jintercept=True)
- 通过正规方程优化
fit_ _intercept: 是否计算偏置LinearRegression.coef:回归系数LinearRegression.intercept:偏置
6.1 sklearn.linear. model.SGDRegressor(loss="squared_ loss", fit_ jintercept=True, learning. _rate='invscaling', eta0=0.01)
SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回
归模型。loss:损失类型
loss="squared_ loss": 普通最小二乘法fit _intercept:是否计算偏置learning_ rate: string, optional
- 学习率填充
constant: eta = eta0optimal: eta = 1.0/ (alpha * (t + to)) [default]invscaling: eta = eta0 / pow(t, power, _t)power_ _t=0.25:存在父类当中- 对于一个常数值的学习率来说,可以使用learning. _rate=‘constant’,并使用eta0来指定学
习率。SGDRegressor.coef_:回归系数SGDRegressor.intercept:偏置
7、回归性能评估
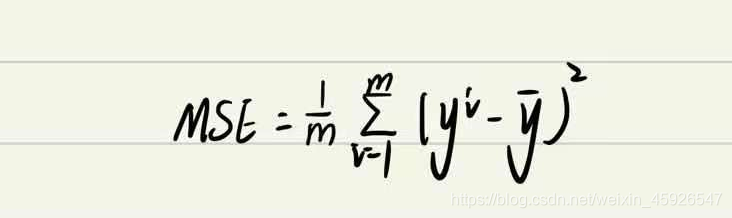
- yi:为预测值;
- y-:为真实值。
7.1 API
sklearn.metrics.mean_squared_error(y_true, y_pred):
- 均方误差回归损失;
y_true:真实值;y_pred:预测值;return:浮点数结果。
8、案例
# -*- coding: utf-8 -*-
""" @Time : 2021/08/02 16:24
@Author : XXX
@Site :
@File : 2.波士顿房价.py
@Software: PyCharm
"""
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error
def model1():
"""线性回归模型"""
# 获取数据
data = load_boston()
# 数据基本处理
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)
# 特征工程
stand = StandardScaler()
x_train = stand.fit_transform(x_train)
x_test = stand.fit_transform(x_test)
# 建立模型
estimator = LinearRegression()
estimator.fit(x_train, y_train)
# 模型评估
pre = estimator.predict(x_test)
print("预测值:", pre)
score = estimator.score(x_test, y_test)
print("准确率:", score)
# 均方误差
ret = mean_squared_error(y_test, pre)
print("均方误差是", ret)
def model2():
"""梯度下降模型"""
# 获取数据
data = load_boston()
# 数据基本处理
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)
# 特征工程
stand = StandardScaler()
x_train = stand.fit_transform(x_train)
x_test = stand.fit_transform(x_test)
# 建立模型
"""
squared_loss:指的是普通的最小二乘拟合。
huber:修改了squared_loss,减少了对异常值的关注经过一段距离后,由平方转换为线性损耗进行校正ε。
epsilon_insensitive:忽略小于epsilon的错误线性的过去; 这是SVR中用到的损失函数。
squared_epsilon_insensitive:是相同的,但成为平方损失过去的容差。
"""
estimator = SGDRegressor(learning_rate='constant', random_state=20)
estimator.fit(x_train, y_train)
# 模型评估
pre = estimator.predict(x_test)
print("预测值:", pre)
score = estimator.score(x_test, y_test)
print("准确率:", score)
# 均方误差
ret = mean_squared_error(y_test, pre)
print("均方误差是", ret)
if __name__ == '__main__':
model1()
model2()