环形链表I

解题分析示例

https://leetcode-cn.com/problems/linked-list-cycle/description/
问题：给定一个链表，判断链表中是否有环。
思路：方法1：此问题是链表中的经典问题，用的也是经典方法：快慢针；这也是南京邮电大学2021年计算机考研811数据结构算法题的第一题，别问我怎么知道的，问就是本人考过呜呜。
方法2：其实如果不算空间复杂度和时间复杂度，是可以用一个很长的数组存起来走过的每一个结点的地址，走到下一个结点时再去遍历数组看看有没有相同的结点来判断是否有环。

快慢针过程如下图举例所示

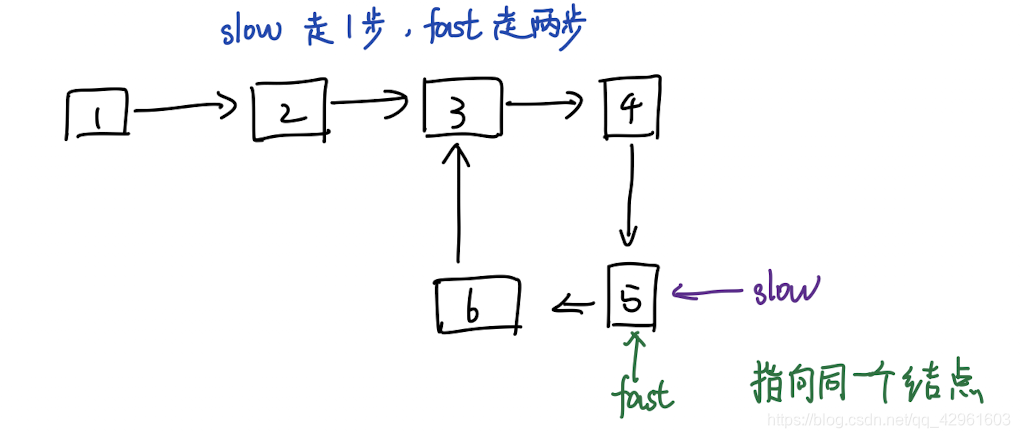
在这里插入图片描述

代码如下

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    struct ListNode *slow = head;
    struct ListNode *fast = head;
    while(fast != NULL && fast->next != NULL){
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow){
            return true;
        }
    }
    return false;
}

面试提问

面试提问
1、slow一次走一步，fast一次走两步，一定可以追上吗？请证明。
2、slow一次走一步，fast一次走n步呢？（n=3,4,5…）

1、一定可以追上。
如下图所示，我们假设环的一圈有C个结点，慢指针slow刚进环时，快指针fast在顺时针方向上（快追慢）与slow相差N个结点。快慢指针各走一次即可缩短一个结点的距离，最终N为0时，slow和fast相遇。
在这里插入图片描述

2、不一定。
假设慢指针slow刚入环时，fast与slow相距的结点数为N，环一圈有C个结点；slow每次走1步，fast每次走3步。
在这里插入图片描述
I. 若N为偶数，则slow每次走1步，fast每次走3步，则每次移动过后fast与slow之间的距离就减少2；N为偶数，则一定可以正好将距离减少到0，即相遇。
II. 若N为奇数，每次移动距离减少2，则会使得距离在某次移动过后出现-1，这代表fast指针超过了slow一个位置，按照快追慢原则，fast此时在顺时针方向上与slow相距C-1；若C是奇数，C-1就是偶数，fast与slow相差偶数个单位的距离，且每次移动fast都能将距离缩小2，则问题此时变得与问题1相似，一定会相遇。若C是偶数，C-1就是奇数，则问题就回到开始N为奇数时的那个问题，这种情况，fast和slow就永远不可能相遇。

环形链表II

https://leetcode-cn.com/problems/linked-list-cycle-ii/
给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。
先说结论：让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环运行，两个指针都是每次均走一步，最终肯定会在入口点的位置相遇。
再给代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *slow = head;
    struct ListNode *fast = head;
    //pos1用来从slow与fast相遇点开始走
    //pos2用来与pos1对应，从链表开头位置开始走
    //最终pos1与pos2相遇的地方就是链表的环的第一个结点
    struct ListNode *pos1 = NULL; 
    struct ListNode *pos2 = NULL
    while(fast!=NULL && fast->next!=NULL){
        fast = fast->next->next;
        slow = slow->next;
         if(fast == slow){
            pos1 = fast;
            break;
         }
    }
    if(pos1 != NULL){
        pos2 = head;
        while(pos1 != pos2){
            pos2 = pos2->next;
            pos1 = pos1->next;
        }
        return pos1;
    }else{
        return NULL;
    }
}