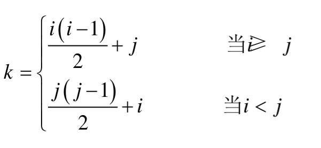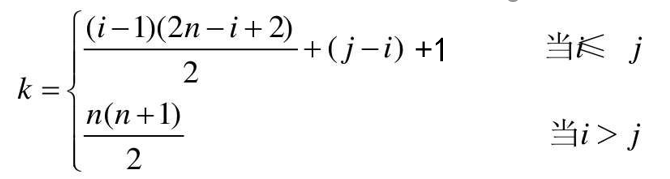对称矩阵

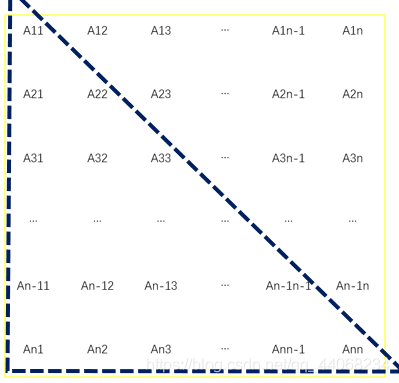
若n阶矩阵满足a ij = a ji （1<=i,j<=n），称为n阶对称矩阵。

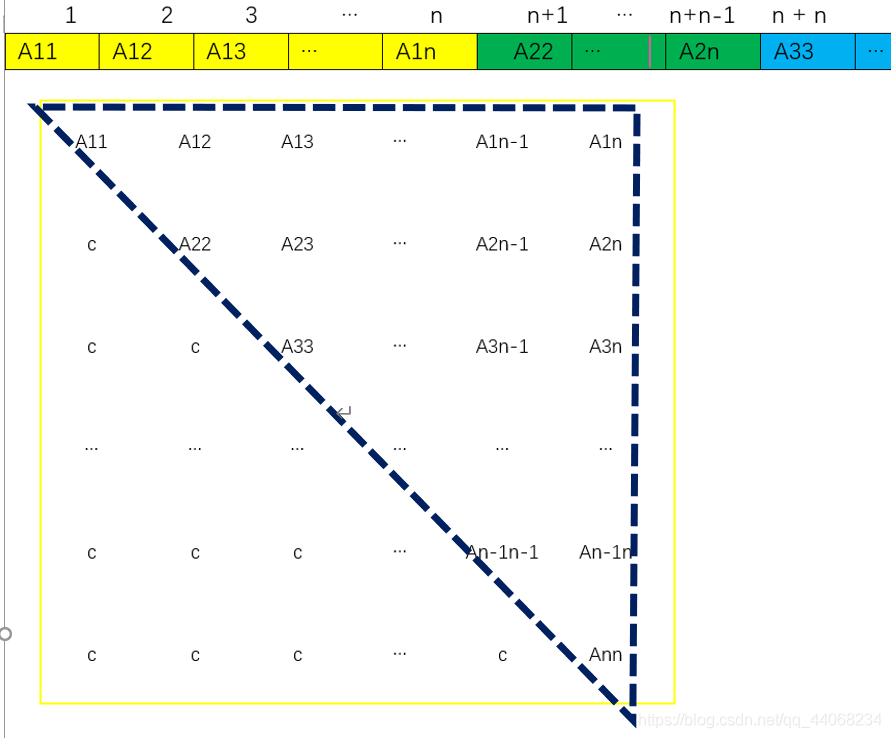
若n阶矩阵为对称矩阵，那么实现压缩存储，只需要对矩阵的含对角线的上三角进行存储。（如图的虚线框内）对于对称矩阵可以用上三角也可以用下三角，下三角的表达式容易推导，所以采用下三角，想用上三角的可以参考三角矩阵的内容。

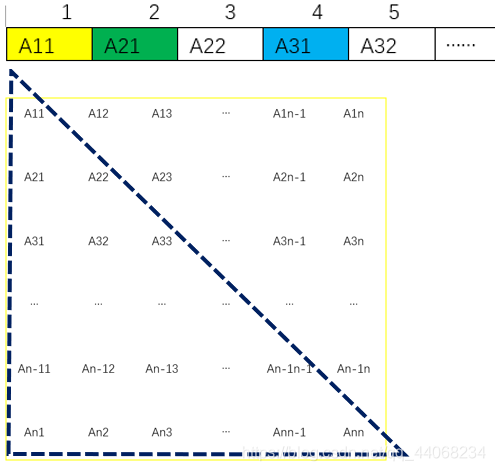
我们需要把虚线框内的元素对应到一维数组，来找寻aij在一维数组中的位置。方便理解，一维数组从B[1]开始。

要求对称矩阵压缩到一维数组B[ k ]，我们需要知道
（1）需要存储的元素数目
（2）矩阵元素aij 与B[ k ]中的k值的对应关系

（1）矩阵第i行有i个元素，1<=i<=n，即元素总和为n*(n+1)/2
（2）观察第 i 行的起始位置对应k值

i=1 , k=1 —> a1=1
i=2 , k=2 —> a2=a1+1
i=3 , k=4 —> a3=a2+2
i=4 , k=7 —> a4=a3+3

则 an = an-1 + n-1
得推导式
an = n * (n-1)/2 + 1
即 ai = i * (i-1)/2+1
又因为j是第i行的偏移量，所以
k = i * (i-1)/2+1+(j-1) ----> k = i * (i-1)/2+j
而上三角的内容因为a ij = a ji （1<=i,j<=n），所以将j映射为i即可。
最后得到表达式

三角矩阵

三角矩阵有上三角矩阵和下三角矩阵之分，上三角矩阵是指矩阵下三角（不含对角线）的元均为常数或者零的n阶矩阵。

下三角矩阵
在对称矩阵的存储中就用的是下三角矩阵，得到的公式为：
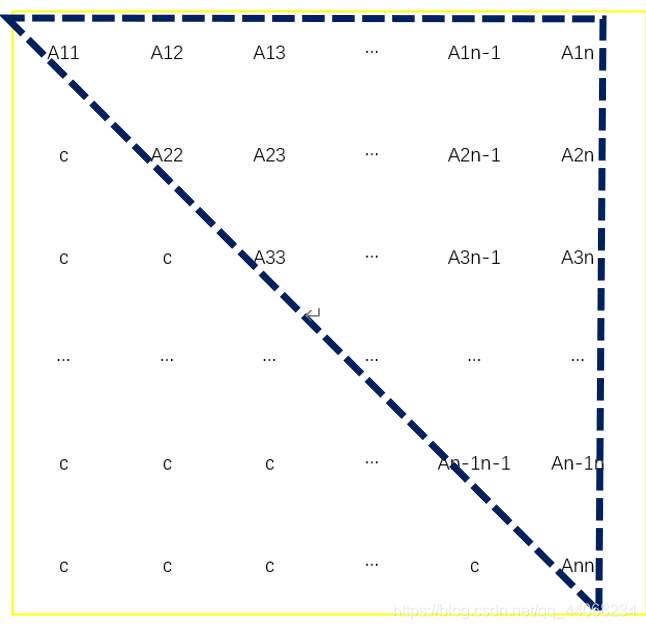
上三角矩阵

下三角为常数c或零的矩阵

类似的，要求上三角矩阵压缩到一维数组B[ k ]，我们需要知道
（1）需要存储的元素数目
（2）矩阵元素aij 与B[ k ]中的k值的对应关系

（1）矩阵第i行有i个元素，1<=i<=n，即元素总和为n*(n+1)/2
（2）观察第 i 行的起始位置对应k值

i=1 , k=1 —> a1=1
i=2 , k=n+1 —> a2=a1 + n
i=3 , k=n+n-1+1 —> a3=a2 + n-1
i=4 , k=n+n-1+n-2+1 —> a4=a3 + n-2

则 am = am-1 + n - (m-2)
得推导式
am = (m-1) * n + 1 - ( 1+2+3+…m-2 ) ===>
am = (m - 1) * (2n - m + 2) / 2 +1
即
ai = (i - 1) * (2n - i + 2) / 2 +1
又因为j - i是第i行的偏移量，所以
k = (i - 1) * (2n - i + 2) / 2 +1 +( j - i)
最后得到表达式

对角矩阵

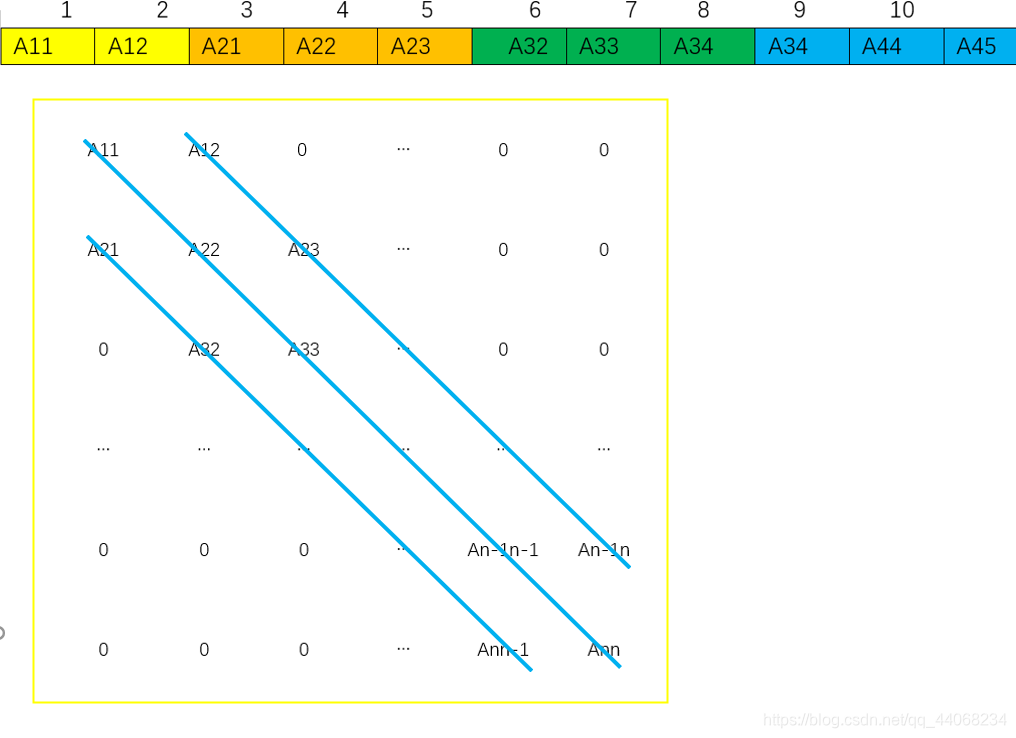
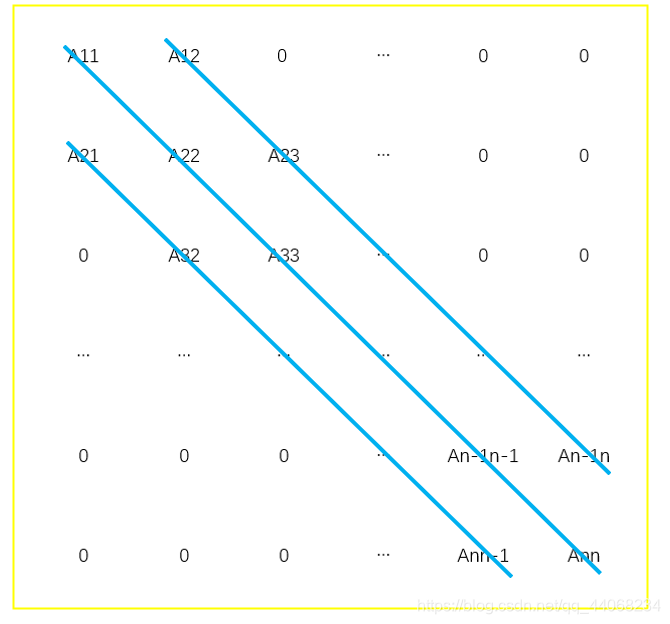
对角矩阵的所有非零元素都集中在以主对角线为中心的带状区域中，其他都为零。下面讲述常见的三对角矩阵，m条对角线的n阶对角矩阵压缩存储的通用寻址公式请参考知网论文
在这里插入图片描述
类似的，要求上三角矩阵压缩到一维数组B[ k ]，我们需要知道
（1）需要存储的元素数目
（2）矩阵元素aij 与B[ k ]中的k值的对应关系

（1）矩阵第1和n行有2个元素，其中行都是3个元素，即元素总和为3*n-2
（2）观察对应关系

观察主对角线上的元与k值
i=1 , k=1 —> a1=1
i=2 , k=4 —> a2=a1+3
i=3 , k=7 —> a3=a2+3
i=4 , k=10 —> a4=a3+3
即ai = 3*(i-1) + 1
则当i = j 时，即主对角线元
k = 3*(i-1) + 1 … (1)
而当i = j - 1时，即主对角线元右边的元（一行三个元）
k = 3*(i-1) + 2 … (2)
而当i = j +1时，即主对角线元左边的元
k = 3*(i-1) … (3)
综合三个式子得到式子：