[数据结构与算法]八大排序算法

八大排序算法

最近在学习排序算法，主要以韩顺平的数据结构为主，并搜索了其他的一部分资料进行整理（因为时间挺久，忘了资料的出处，我就不贴出原博客了，有侵权私我删），然后自己将排序算法实现了一遍，可能会有不少的错误，还请各位dalao指出错误

冒泡排序

冒泡排序
int temp;
boolean flag = false;   //用来防止已排序好的数组还进行循环
for(int j = 0;j < nums.length - 1;j++){
    for (int i = 0; i < nums.length - 1 - j; i++) {
        if (nums[i] > nums[i + 1]) {
            flag = true;    //标记为交换过
            temp = nums[i];
            nums[i] = nums[i + 1];
            nums[i + 1] = temp;
        }
    }
    if(!flag){  //未交换过，说明已经排序好了
        break;
    }else {     //交换过，再将标记设置为false，防止下一次为排序好的
        flag = false;
    }
    System.out.println(Arrays.toString(nums));

选择排序

选择排序(select sorting) 也是一种简单的排序方法。它的基本思想是:第 一次从arr[0]~arr[n-1]中选取最小值，与arr[0]交换， 第二次从 arr[1]~ arr [n-1]中选取最小值，与arr[1]交换， 第三次从arr[2] arr [n-1]中 选取最小值，与arr[2]交换， …， 第i次从arr[i-1]~arr[n-1]中选取最小值， 与arr[i-1]交换， 第n-1次从arr[n-2]arr[n-1]中选取最小值，与arr[n-2] 交换，总共通过n-1次，得到一个按排序码从小到大排列的有序序列。

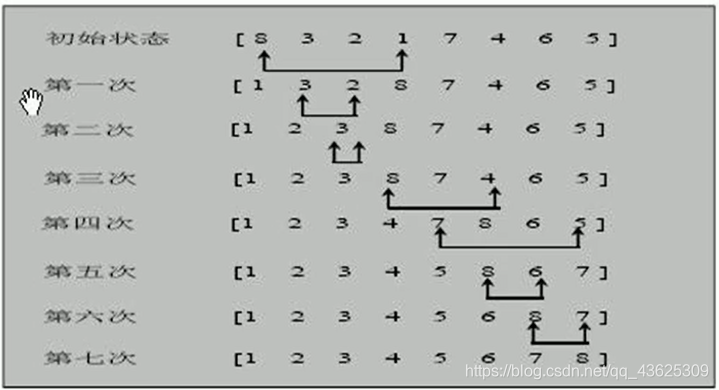
选择排序
for(int i = 0;i < 4;i++){
    int min = nums[i];
    int temp;
    for(int j = i + 1;j < 5;j++ ){
        if(min < nums[j]){
            min = nums[j];
            temp = j;   //表示最小值的位置
        }
    }
    if(temp != i){
        nums[temp] = nums[i];
        nums[i] = min;
    }
    System.out.println( Arrays.toString(nums));
}

插入排序

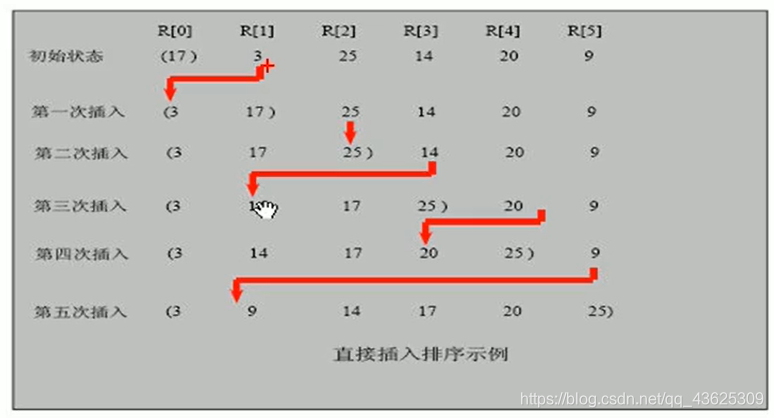
插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中 包含有n-1个元素，排序过程中每次从无序表中取出第-一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的 适当位置，使之成为新的有序表。

插入排序
for(int i = 1;i < nums.length;i++){
    int temp;
    for(int j = 0;j <= i-1;j++){
        if(nums[i] > nums[j]){
            temp = nums[i];     //记住要插入的值
            for(int k = i;k > j;k--){
                nums[k] = nums[k-1];
            }
            nums[j] = temp;
        }
    }
    System.out.println(Arrays.toString(nums));

希尔排序

希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序是一种插入排序，它是简单插入排序经过改进之后的一一个更高效的版本，也称 缩小增量排序。
希尔排序法基本思想
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序;随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止

希尔排序
for(int gap = nums.length / 2;gap > 0;gap /= 2){
    for(int i = gap;i < nums.length;i ++){
        int j = i;
        int temp = nums[j];
        if(nums[j] < nums[j-gap]){
            while(j - gap >= 0 && temp < nums[j-gap]){
                //移动
                nums[j] = nums[j-gap];
                j -= gap;
            }
            //当退出循环后就找到给temp插入的位置
            nums[j] = temp;
        }
    }
    System.out.println(Arrays.toString(nums));
}
System.out.println(Arrays.toString(nums));

快速排序

快速排序(Quicksort) 是对冒泡排序的一种改进。基本思想是:通过一一走道 序将要排序的数据分割成独立的两部分，其中一部分
的所有数据都比另外-部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

快速排序的右指针需要先向左动

为什么是右边指针先动？

来个极端案例，比如，第一个数就是最小的数，如果先让左指针动，左指针是遇到大于key的值才停下，此时其实左指针多往右跑了一步，到第二个位置才会停下，因为谁先动就会先判断谁，所以最终结果是左右指针相遇在第二个位置，第一个数其实和第二个数交换了，向后错了一位。所以，如果左指针先动的话，其实，最终，把第一个基准数和左右指针相遇时的位置交换这一步会出错，左右指针比应该原本应该相遇的位置右移一位。

快速排序
public static void quickSort(int[] nums,int l,int r){
    if(l >= r){
        return;  //递归出口,前后指针相遇
    }
    int key = l ,i,j,temp;    //key为基准,i为左边指针，r为右边指针
    i = l;
    j = r;
    while(i < j){
        //注意：这里必须先从右向左
        while(nums[j] >= nums[key] && i < j){
            j--;//右指针遇到小于key的停下
        }
        while(nums[l] <= nums[key] && i < j){
            i++;//左指针遇到大于key的停下
        }
        if(i < j){      //当两边都停下时，交换
            temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
        }
    }
    temp = nums[key];       //交换基准数和相交时的数
    nums[key] = nums[i];
    nums[i] =temp;
    count++;
    System.out.print("count:"+count);
    System.out.println(Arrays.toString(nums));
    quickSort(nums,l,i-1);   //将左边的数组排序
    quickSort(nums,i+1,nums.length-1);  //将右边的数组排序
}

归并排序

归并排序(MERGE- SORT)是利用归并的思想实现的排序方法，该算法采用经典的分治(divide- and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案修补”在一 起，即分而治之)。

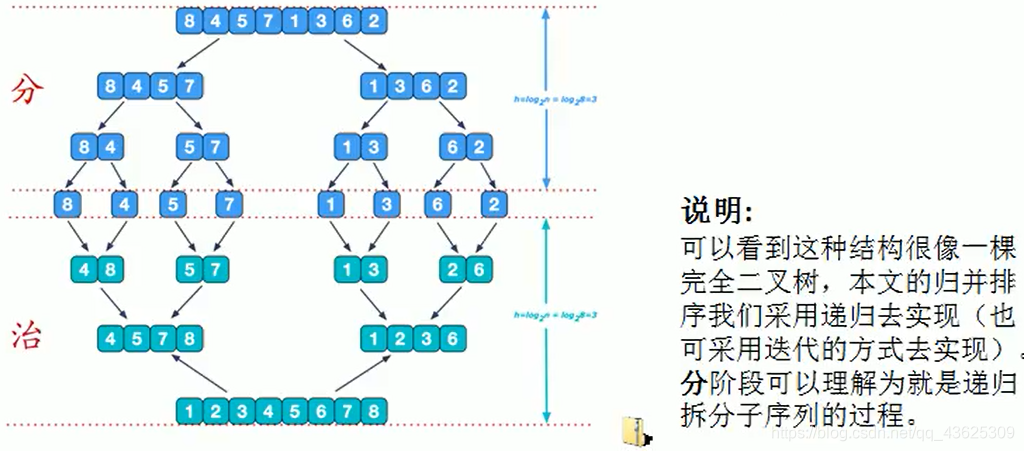
归并排序
public static int[] mergeSort(int[] arr,int left,int right){
    if(left < right){
        int mid = (left + right)/2;
        arr = mergeSort(arr,left,mid);
        arr = mergeSort(arr,mid + 1,right);
        merge(arr,left,mid,right);
    }
    return arr;
}

//将传入的两个数组合并
public static void merge(int[] arr,int left,int mid,int right){
    int temp[] = new int[right - left + 1];     //创建一个临时数组
    int i = left,j = mid+1;    //i表示左边数组的标记，j表示右边数组的标记
    int key = 0;    //表示新数组的当前坐标
    while(i <= mid && j <= right){  //当两个数组的指针都小于长度时
        if(arr[i] < arr[j]){
            temp[key++] = arr[i++];
        }else {
            temp[key++] = arr[j++];
        }
    }
    while(i <= mid){
        temp[key++] = arr[i++];
    }
    while(j <= mid){
        temp[key++] = arr[j++];
    }

    for(int p =0;p < key;p++){  //数组赋值
        arr[left++] = temp[p];
    }
    System.out.println(Arrays.toString(arr));
}

基数排序

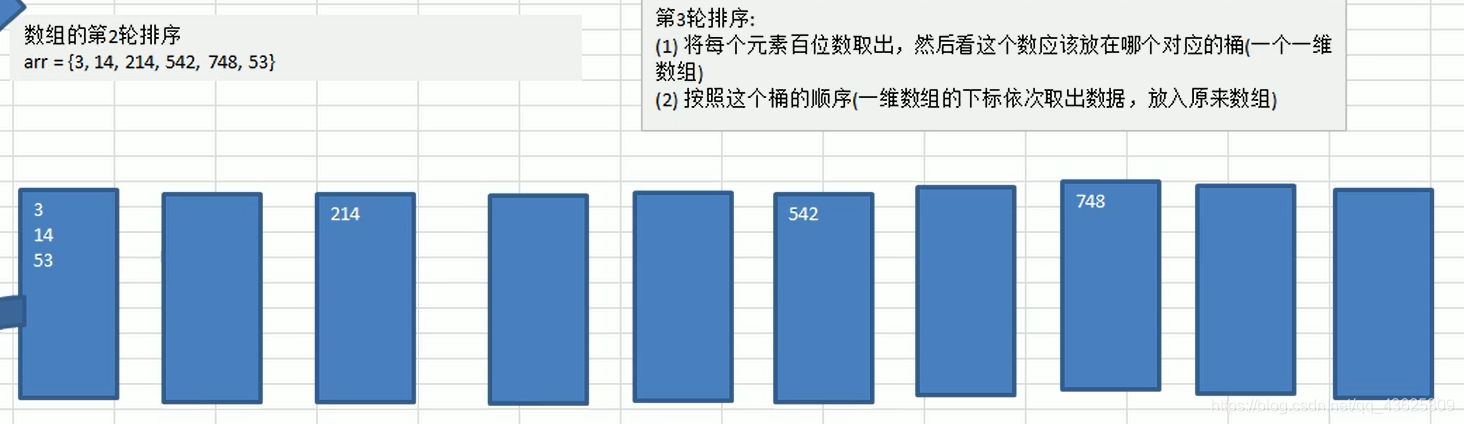
1)基数排序(radixsort) 属于“分配式排序”(distributionsort) ，又称子法”(bucket
sort)或binsort， 顾名思义，它是通过键值的各个位的值，将要排序的元素分配至某些“桶”中，达到排序的作用
2)基数排序法是属于稳定性的排序，基数排序法的是效率高的稳定性排序法
3)基数排序(Radix Sort)是桶排序的扩展
4)基数排序是1887年赫尔曼:何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字，然后按每个位数分别比较。

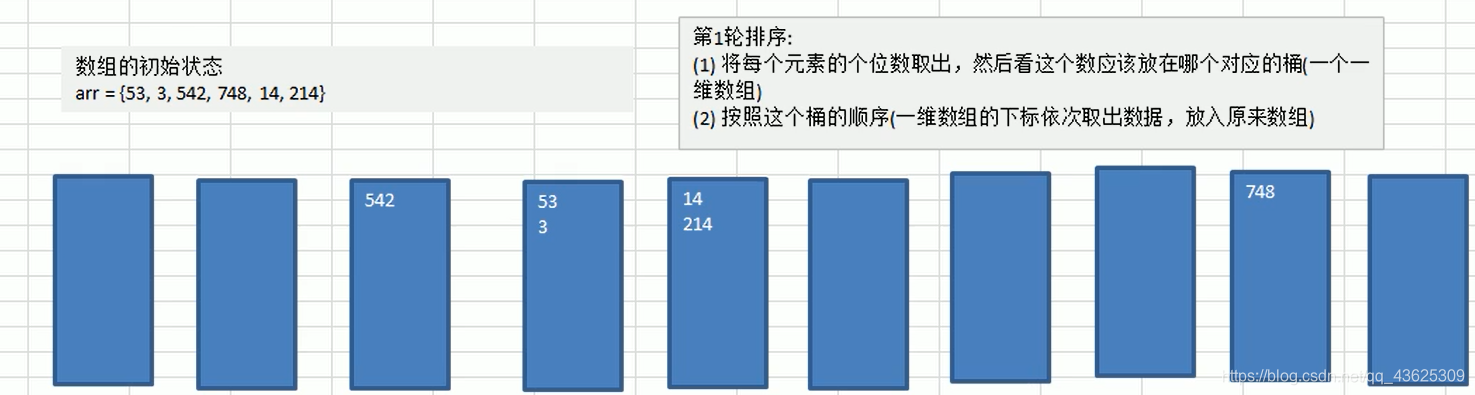
基数排序
public static void radixSort(int arr[]){
    //求取该数组的最高位
    int max = arr[0],maxLength = 1;
    for(int i =1;i <arr.length;i++){
        if(arr[i] > max)
            max = arr[i];
    }
    while(max/10 != 0){
        max /= 10;
        maxLength++;
    }

    //创建桶数组
    int[][] bucket = new int[10][arr.length];
    //记录每个桶放入的数据个数
    int[] bucketCount = new int[10];

    //从第一位开始比较，直到比较到最高位
    //n表示当前要除n倍来求余数
    for(int i = 1,n = 1;i <= maxLength;i++,n *= 10){
        for(int j = 0;j < arr.length;j++){
            int temp = arr[j]/n %10;    //每个数当前位数的数字
            bucket[temp][bucketCount[temp]] = arr[j];
            bucketCount[temp]++;
        }

        //使用index来表示原数组的下标
        int index = 0;
        //根据桶从小到大的顺序将值给原数组
        for(int k = 0;k < 10;k ++){
            //如果桶中有数据才循环放入数组
            if(bucketCount[k] != 0){
                //循环第k个桶的值并赋值给原数组
                for(int l = 0;l < bucketCount[k];l++){
                    arr[index++] = bucket[k][l];
                }
                bucketCount[k] = 0;
            }

        }
        System.out.println(Arrays.toString(arr));
    }
}

堆排序

1)堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序,它的最坏，最好，平均时间复杂度均为0(nlogn)，它也是不稳定排序。
2)堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆,注意:没有要求结点的左孩子的值和右孩子的值的大小关系。
3)每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆

自己实现的堆排序，还需要优化

public static int[] heapCreate(int[] arr,int length){
    //用来构造大顶堆
    for(int i = 1;i < length;i ++){
        int temp = i;
        while((temp-1)/2 >= 0){   //一直循环到最后一个节点或者小于某个父节点
            if(arr[temp] > arr[(temp-1)/2]){
                swap(arr,temp,(temp-1)/2);
                //System.out.println(Arrays.toString(arr));
            }else {
                break;
            }
            //再次循环看父节点
            temp = (temp - 1) / 2;
        }
    }
    System.out.println("构造好的大顶堆：" + Arrays.toString(arr));
    return arr;
}

public static void heapSo(int[] arr){
    //用来将大顶堆排序
    int length = arr.length - 1;
    for(int i = length;length >= 0;i--,length--){
        swap(arr,i,0);
        heapCreate(arr,length);
    }
    System.out.println(Arrays.toString(arr));
}

public static void heapSort(int[] arr){
    //构造大根堆
    heapCreate(arr,arr.length);
    //大顶堆排序
    heapSo(arr);
}

八个排序算法的比较