现在对十大常用的排序算法做一个总结,便于记忆。
十大排序算法分别是:冒泡排序、快速排序、插入排序、希尔排序、选择排序、堆排序、归并排序、计数排序、基数排序、桶排序,如下图所示:
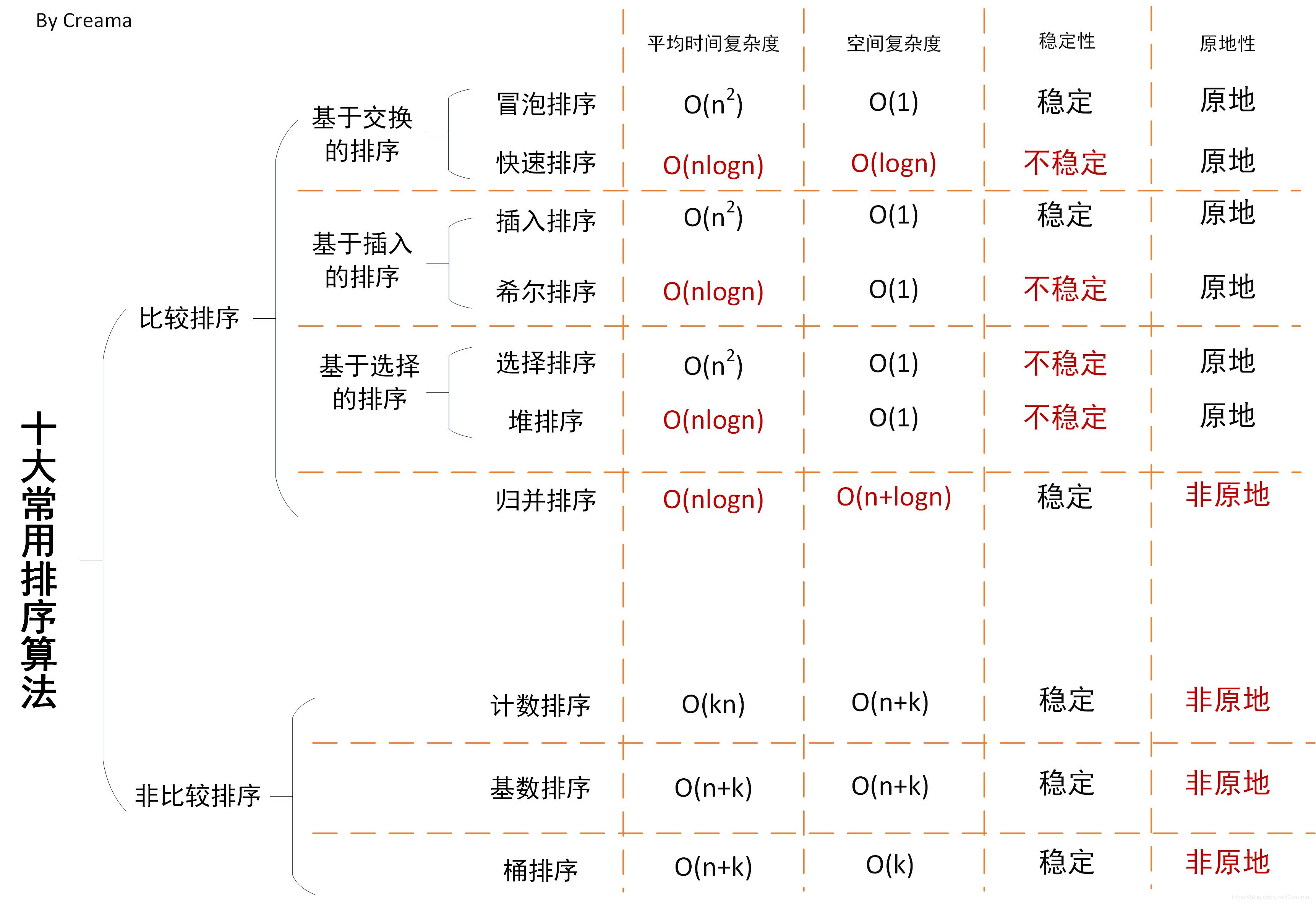
注:
稳定性:相等的两个数,排序后的相对位置和排序前一样。比如原数组中有三个数abA,如果a=A=1,b=2。排序后的结果是aAb,那就是稳定排序,如果排序结果是Aab那就是不稳定排序。
原地性:不重新申请数组,只在原数组上进行比较和交换。
其中前面七种排序是基于比较的排序,后面三种是非比较的排序,或者称为基于统计的排序,这里主要介绍前面七种基于比较的排序。这七种排序方法中,有三种基本的排序方法,分别是冒泡排序(基于交换)、插入排序、选择排序。还有在这三种基本排序方法的基础之上进行排序的方法(改进的方法),分别是快速排序、希尔排序、堆排序,然后归并排序可以分为特殊的一类。
记忆小技巧:
时间复杂度只记四种改进的算法(O(nlogn)):快速、希尔、堆、归并。其他三种都是O(n2),毕竟改进嘛,改的就是时间复杂度。但是可以发现改进后的算法要么不稳定,要么非原地,所以想要快,就要牺牲其他方面。
空间复杂度只记两种不是O(1)的:快速(O(logn))和归并(O(n+logn))。
稳定性只记四种不稳定的算法:快速、希尔、选择、堆。
原地性只记一种非原地算法:归并排序。
几个小问题:
快速排序是原地算法,为什么空间复杂度是O(logn)?
因为快速排序常用递归的方法实现,递归需要系统的栈空间。如果用迭代的方法实现,那就是O(1)空间复杂度。
堆排序也要用递归实现,为什么空间复杂度是O(1)?
和快速排序一样,用迭代的方法实现就是O(1)的,用递归方法实现就是O(logn)的。
下面就这七种排序算法,详细讲一下各自的原理、代码实现(C++)、时间复杂度、空间复杂度、稳定性和原地性,代码都经过测试,有不对的地方欢迎评论。
冒泡排序
原理
冒泡排序是一种交换排序,每一轮通过与相邻的元素交换,将最大值换到当前元素遍历过的元素的末端。(动图来源于网络)
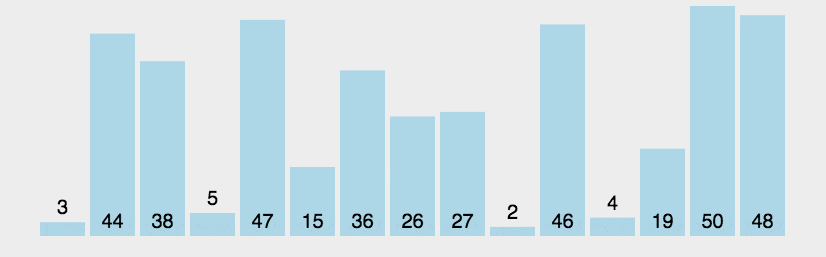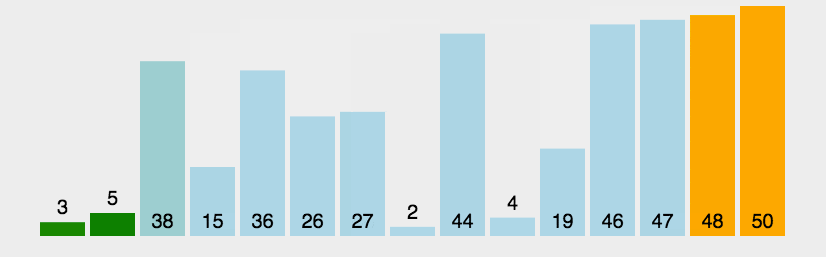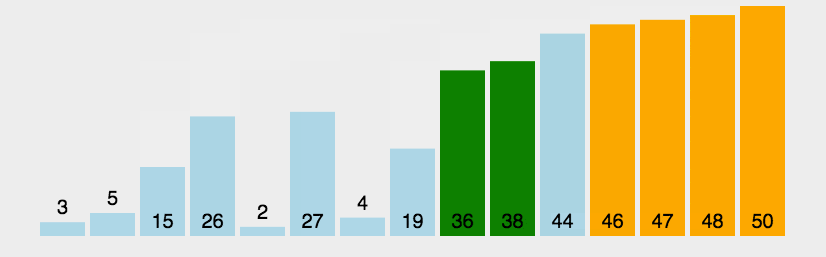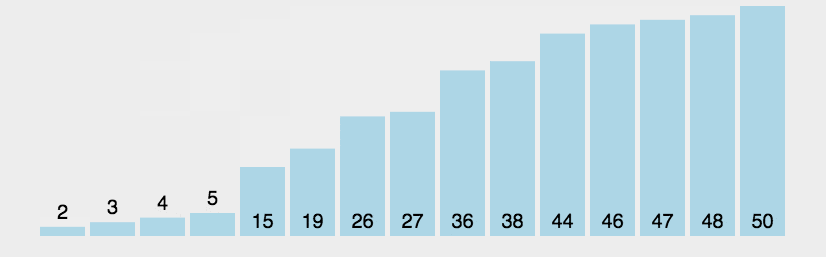
代码实现
void bullleSort(vector<int>& nums) {
//i表示轮次,j表示每轮元素的下标
for (int i = 0; i < nums.size() - 1; i++) {
for (int j = 0; j < nums.size() - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
}
}
}
}
改进1:设置标记位,如果一遍内循环后没有发生交换,说明数组已经排好序,直接返回。
void bullleSort(vector<int>& nums) {
//i表示轮次,j表示每轮元素的下标
for (int i = 0; i < nums.size() - 1; i++) {
bool flag = true;
for (int j = 0; j < nums.size() - 1 - i; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
flag = false;
}
}
if (flag) return ;
}
}
改进2:记录某个内循环最后一次发生数据交换的位置,该位置后面的数肯定已经排好序,下一次遍历到该位置即可。
void bullleSort(vector<int>& nums) {
int last_index = nums.size() - 1; //记录内循环最后一次发生数据交换的位置
//i表示轮次,j表示每轮元素的下标
for (int i = 0; i < nums.size() - 1; i++) {
bool flag = true;
int temp_index = last_index; //每次发生数据交换时更新
for (int j = 0; j < last_index; j++) {
if (nums[j] > nums[j + 1]) {
swap(nums[j], nums[j + 1]);
flag = false;
temp_index = j + 1;
}
}
last_index = temp_index;
if (flag) return;
}
}
性能分析
时间复杂度:平均O(n2),最佳O(n),最差O(n2)
空间复杂度:O(1)
稳定性:稳定
原地性:交换排序,原地
快速排序
原理
快速排序也是交换排序,主要是利用partition函数找到一个基准(pivot),使比pivot小的元素在其左边部分,比pivot大的元素在其右边部分,这样相当于把pivot放到了正确的位置。然后再利用partition函数分别对左右两部分元素进行处理,直到处理的部分长度为1。
代码实现
int partition(vector<int>& nums, int left, int right) {
int pivot = nums[left]; //一般取第一个元素
int i = left, j = right + 1; //i=left,j=right,因为下面while里面是++i,--j,即使得第一次循环的双指针分别是left+1和right
while (true) {
while (nums[++i] < pivot && i < right);
while (nums[--j] > pivot && j > left);
if (i >= j) break;
//到这里说明,nums[i]>=pivot并且nums[j]<=pivot,需要把nums[i]放到左边,把nums[j]放到右边部分,通过交换实现
swap(nums[i], nums[j]);
}
//这里要把pivot放到正确的位置,与nums[j]交换是因为,到这里说明i>=j,此时nums[j]<=pivot
swap(nums[left], nums[j]);
return j;
}
void quickSort(vector<int>& nums, int left, int right) {
if (left >= right) return;
int index = partition(nums, left, right);
quickSort(nums, left, index - 1);
quickSort(nums, index + 1, right);
}
int main() {
vector<int> arr = {1, 4, 5, 6, 0, 4, 5, 56, 333, 4, 6, 9, 53};
quickSort(arr, 0, arr.size()-1);
for (auto a : arr) {
cout << a << endl;
}
return 0;
}
改进:递归改迭代。有时间再写
性能分析
时间复杂度:平均O(nlogn),最佳O(nlogn),最差O(n2)
空间复杂度:O(logn),递归使用栈空间
稳定性:不稳定,比如3141’,这里1’表示和前面一个1区分,swap(nums[i], nums[j])后变成311’4,swap(nums[left], nums[j])后变成1’134,这就不稳定了。
原地性:原地
插入排序
原理
插入排序有点像打扑克牌时的理牌过程,从左开始依次处理每张牌,把这张牌插到前面正确的位置上,只不过代码实现上使用移位来实现。插入排序适用于数据量小的情况,特别是基本上排好序的情况。
代码实现
void insertSort(vector<int>& nums) {
//一个for循环
for (int i = 1; i < nums.size(); i++) {
int pre_index = i - 1, temp = nums[i];
while (pre_index >= 0 && nums[pre_index] > temp) {
nums[pre_index + 1] = nums[pre_index]; //后移
--pre_index;
}
//pre_index+1是因为,pre_index < 0 或者 nums[pre_index]<=temp,要往后一位插入
nums[pre_index+1] = temp;
}
}
改进1:在往前找合适的插入位置时使用二分查找,找到后仍然要挨个移动元素,提升不明显。
改进2:希尔排序。
性能分析
时间复杂度:平均O(n2),最佳O(n),最差O(n2)
空间复杂度:O(1)
稳定性:稳定
原地性:原地
希尔排序
原理
希尔排序就是分组插入排序,又称递减增量排序算法。因为插入排序对几乎已经排好序的数组排序时,效率很高,所以可以将整个数组,按某个间隔分割成若干个子序列,先对这些子序列排序,然后减小间隔继续排序,等间隔为1时整个数组基本有序,最后对所以元素进行一次直接插入排序即可。(帅地的图)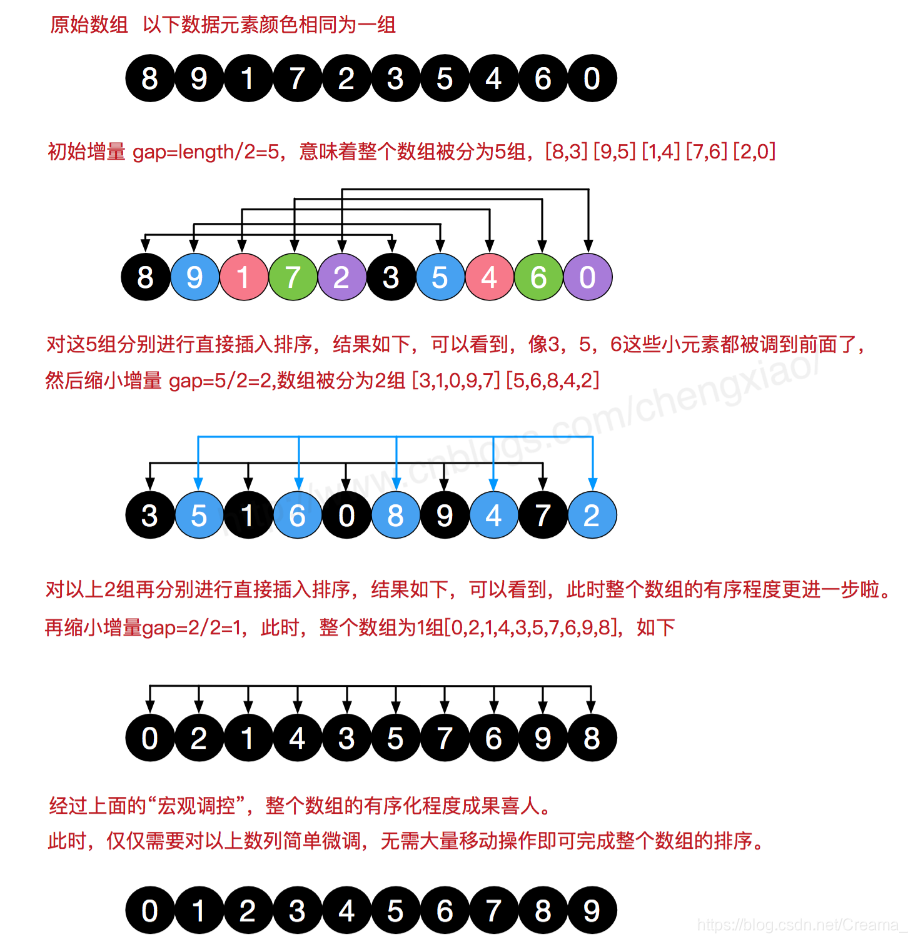
代码实现
void shellSort(vector<int>& nums) {
//在插入排序外面再嵌套一个for循环
for (int gap = nums.size() / 2; gap > 0; gap /= 2) {
//插入排序的for循环
for (int i = gap; i < nums.size(); i++) {
int pre_index = i - gap, temp = nums[i];
while (pre_index >= 0 && nums[pre_index] > temp) {
nums[pre_index + 1] = nums[pre_index]; //后移
pre_index -= gap;
}
nums[pre_index + gap] = temp;
}
}
}
可以发现,插入排序不过是希尔排序在的gap=1的情况下的排序算法,所以只要在插入排序外面再嵌套一个for循环,把1换成gap,就可以了,希尔排序还有另外一种写法,不过我比较喜欢这种,毕竟记一种就相当于记两种排序算法了。
性能分析
时间复杂度:平均O(nlogn),最佳O(n),最差O(n2)
空间复杂度:O(1)
稳定性:不稳定
原地性:原地
选择排序
原理
代码实现
性能分析
时间复杂度:
空间复杂度:
稳定性:
原地性:
堆排序
原理
代码实现
性能分析
时间复杂度:
空间复杂度:
稳定性:
原地性:
归并排序
原理
代码实现
性能分析
时间复杂度:
空间复杂度:
稳定性:
原地性: