[数据结构与算法]排序算法（三）选择排序

基本思想：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的
数据元素排完 。

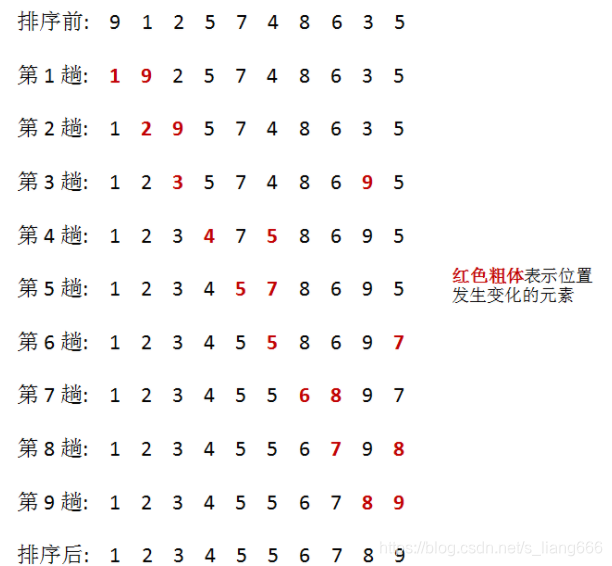
1、直接选择排序

思想：（1）从待排序序列中，找到关键字最小的元素；
（2）如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；
（3）从余下的 N - 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束。

//直接选择排序
void SelectSort(int arr[], int n)
{
	for (int i = 0; i < n; ++i)
	{
		int min_val = arr[i];
		int pos = 0;          //记录最小值位置，方便后面的交换
		for (int j = i+1; j < n; ++j)
		{
			//从后面的数选出一个最小值，并记录位置
			if (min_val > arr[j])
			{
				min_val = arr[j];
				pos = j;
			}
		}
		if (pos != 0)
		{
			//不等于0，证明有最小值
			arr[pos] = arr[i];
			arr[i] = min_val;
		}
	}
}

直接选择排序的特性总结：

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

2、堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。
堆是一棵顺序存储的完全二叉树。其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小堆。其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大堆。
举例来说，对于n个元素的序列{R0, R1, … , Rn}当且仅当满足下列关系之一时，称之为堆：
Ri <= R2i 且 Ri <= R2i+1 (小堆)
Ri >= R2i 且 Ri >= R2i+1 (大堆)，其中i=1,2,…,n/2向下取整；
实现堆排序需要解决两个问题：
（1）如何由一个无序序列建成一个堆？
（2）如何在输出堆顶元素之后，调整剩余元素成为一个新堆？
（一）建小堆过程
对于无序序列{49，38，65，97，76，13，27，49}，主要过程如下：
（1）根据原始数组去构造初始堆，也就是构建一个完全二叉树；
（2）假设序列有n个元素，则筛选从第n/2(向下取整）个元素开始调整。例如上述有8个元素的无序序列，则筛选从第4个元素开始调整，即97开始调整，保证它的值要不大于它的左右结点，由于97>49,则交换之；同理，后面的元素第3,2…个，均按这样的方式进行调整。如下图所示：

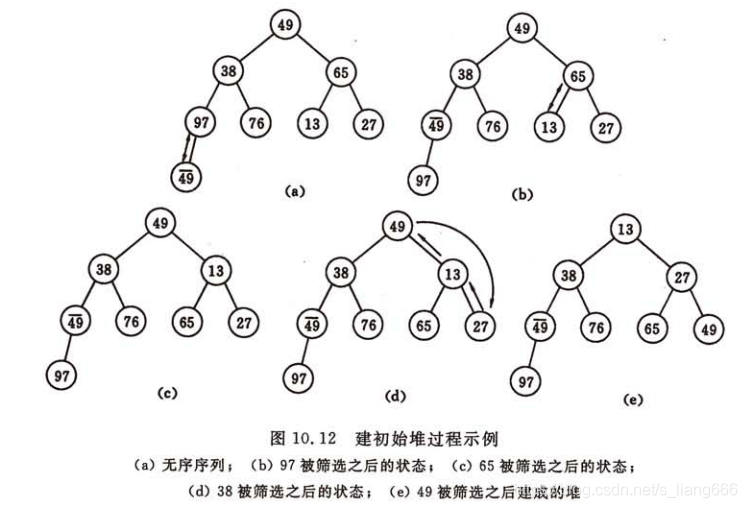
（二）输出堆顶元素，调整建立新堆
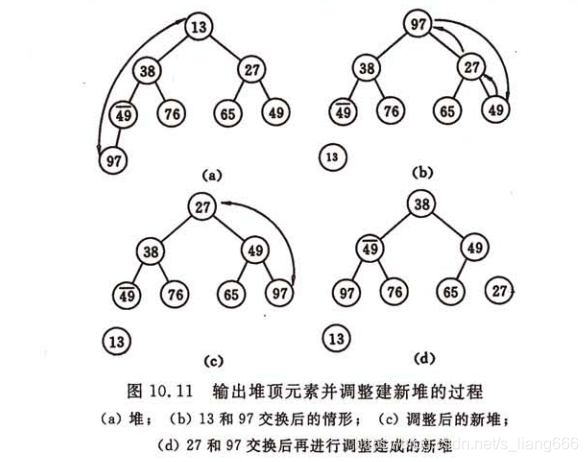
（1）输出堆顶元素，以堆中最后一个元素替代之，此时根结点左右子树均为堆，则仅需自上至下调整即可；
（2）以堆顶元素和其左右子树的根结点比较，由于右子树根结点的值小于左子树根结点的值且小于根结点的值，则将27和97交换之；
（3）由于97替代了27之后破坏了右子树的结构，则和上述相同的调整，直至叶子结点，此时堆顶为n-1个元素的最小值；
（4）重复上述操作（1）（2）（3）输出全部元素为止；

//调整大堆进行升序排列
//向下调整
void _AdjustDown(int arr[], int first, int last, int start)
{
	int n = last - first;
	int i = start;     //开始的下标
	int j = 2 * i + 1; //对应的左子树位置
	int tmp = arr[i]; 
	while (j < n)
	{
		//如果有右子树,并且右子树大于左子树
		if (j + 1 < n && arr[j] < arr[j + 1])
			++j;
		if (tmp < arr[j])
		{
			//调大堆，小的话就交换
			arr[i] = arr[j];
			i = j;
			j = 2 * i + 1;
		}
		else
			break;
	}
	arr[i] = tmp;
}
//堆排序
void HeapSort(int arr[], int first, int last)
{
	//arr[] = { 49, 38, 65, 97, 76, 13, 27, 49}
	//调整成大堆
	int n = last - first;
	//从下标为n/2-1开始调整，即下标为3，第4个元素开始调整
	int curpos = n / 2 - 1;
	while (curpos >= 0)
	{
		_AdjustDown(arr, first, last, curpos);
		curpos--;
	}
	//排序
	//先是最后一个元素与堆顶元素交换，再依次从堆顶元素向下调整成大堆
	int end = last - 1;
	while (end > first)
	{
		Swap(&arr[end], &arr[first]);
		end--;                           //交换并输出，就是下标向前一步
		_AdjustDown(arr, first, end + 1, first);
	}
}

堆排序的特性总结：

1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定