[数据结构与算法]【学习笔记】【Leetcode 分门别类讲解】——栈、队列、优先队列

栈、队列、优先队列相关总结

1、基础使用

【20. 有效的括号】

遇到左括号入栈，当遇到匹配的右括号时，将这对括号出栈，如果最后栈为空，那么它是有效的括号，反之不是。

class Solution {
public:
    bool isValid(string s) {
        stack<char> sk;
        for(char c:s){
            if(c=='(' || c=='{' || c=='[') sk.push(c);
            else{
                switch(c){
                    case(')'):
                        if(sk.empty() || sk.top()!='(') return false;
                        sk.pop();
                        break;
                    case(']'):
                        if(sk.empty() || sk.top()!='[') return false;
                        sk.pop();
                        break;
                    case('}'):
                        if(sk.empty() || sk.top()!='{') return false;
                        sk.pop();
                        break;
                    default: return false;
                }
            }
        }
        if(!sk.empty()) return false;
        return true;
    }
};

【150. 逆波兰表达式求值】

遇到符号pop两个数，将结果push回去，直到运算完

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> s;
        int res;
        for(auto &c:tokens){
            if(c=="+" || c=="-" || c=="*" ||c=="/"){//一定是“”而不是‘’
                int a = s.top();
                s.pop();
                int b = s.top();
                s.pop();
                if(c=="+") res = a+b;
                else if(c=="-") res = b-a;//注意是b-a和b/a
                else if(c=="*") res = a*b;
                else res = b/a;
                s.push(res);
            }
            else s.push(stoi(c));//stoi将 n 进制的字符串转化为十进制
        }
        return s.top();
    }
};

【待做】【71. 简化路径】

2、栈和递归的紧密关系

【144.二叉树的前中后序遍历】

递归：前中后序遍历都很简单

确定递归函数的参数和返回值： 因为要打印出前序遍历节点的数值，所以参数里需要传入vector在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector<int>& vec)

确定终止条件： 在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：

if (cur == NULL) return;

确定单层递归的逻辑： 前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

迭代（栈模拟递归）：普通迭代法和染色法

动画演示

——前序（普通迭代法）：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> s;//注意栈里放的是节点
        if(root==nullptr) return res;
        s.push(root);//中
        while(!s.empty()){
            TreeNode* node = s.top();// 中
            res.push_back(node->val);
            s.pop();
            if(node->right) s.push(node->right);// 右（空节点不入栈）
            if(node->left) s.push(node->left);//左（空节点不入栈）
        }
        return res;
    }
};

——中序（普通迭代法）：

为了解释清楚，我说明一下 刚刚在迭代的过程中，其实我们有两个操作：
处理：将元素放进result数组中
访问：遍历节点
前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};

——后序（普通迭代法）：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

——颜色标记法（染色法）

染色法
核心思想如下：

1. 使用颜色标记节点的状态，新节点为白色，已访问的节点为灰色。
2. 如果遇到的节点为白色，则将其标记为灰色，然后将其右子节点、自身、左子节点依次入栈。
3. 如果遇到的节点为灰色，则将节点的值输出。

其实只需要一个bool值即可，false 代表没经过过这个节点，true 表示已经经过过了，可以处理了。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<pair<TreeNode*,bool>> s;
        if(root==nullptr) return res;
        s.push(make_pair(root,false));//等价于s.push({root,false});
        while(!s.empty()){
            auto [cur,passed] = s.top();
            s.pop();
            if(cur == nullptr) continue;
            if(passed == false){
                s.push(make_pair(cur->right,false));//前序
                s.push(make_pair(cur->left,false));
                s.push(make_pair(cur,true));

                s.push(make_pair(cur->right,false));//中序
                s.push(make_pair(cur,true));
                s.push(make_pair(cur->left,false));

                s.push(make_pair(cur,true));//后序
                s.push(make_pair(cur->right,false));
                s.push(make_pair(cur->left,false));
            }
            else{
                res.push_back(cur->val);
            }
        }
        return res;
    }
};

【待做】【341. 扁平化嵌套列表迭代器】

3、队列问题

——主要为了解决广度优先遍历问题；

——树：层序遍历
——图：无权图的最短路径

3.1、队列与树

——于树而言，广度优先遍历就是层序遍历。

【102&&107&&103. 二叉树的层序遍历 I&&II &&之字型遍历】

队列先进先出，符合一层一层遍历的逻辑，用一个size来控制每一层，
整体框架差不多，根据题意修改答案即可（反转/部分反转）

class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> q;
        if(root==nullptr) return res;
        q.push(root);
        while(!q.empty()){
            int size = q.size();//这里q.size()是会变的，所以要用一个size来记录
            vector<int> vec;//记录每一层的val
            for(int i = 0;i<size;i++){//用size来控制vec记录的是每一层的val
                TreeNode* cur = q.front();
                q.pop();
                vec.push_back(cur->val);
                if(cur->left) q.push(cur->left);
                if(cur->right) q.push(cur->right);
            }
            res.push_back(vec);
        }
        //103就是对结果分奇偶进行reverse
        for(int i = 0;i<res.size();i++){
            if(i%2!=0) reverse(res[i].begin(),res[i].end());
        }
        //107就是反转下答案
        reverse(res.begin(),res.end());
        return res;
    }
};

【199. 二叉树的右视图】

判断是否遍历到单层的最后面的元素 if(i == size -1) res.push_back(cur->val);

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> res;
        queue<TreeNode*> q;
        if(root!=nullptr) q.push(root);
        while(!q.empty()){
            int size = q.size();
            for(int i = 0;i<size;i++){
                TreeNode* cur = q.front();
                q.pop();
                if(i == size -1) res.push_back(cur->val);
                if(cur->left) q.push(cur->left);
                if(cur->right) q.push(cur->right);
            }
        }
        return res;
    }
};

3.2、队列与图

——于图而言，广度优先遍历可以求得无权图最短路径问题；

【279. 完全平方数】

——无法使用贪心

【待做】方法1.动态规划 //链接：

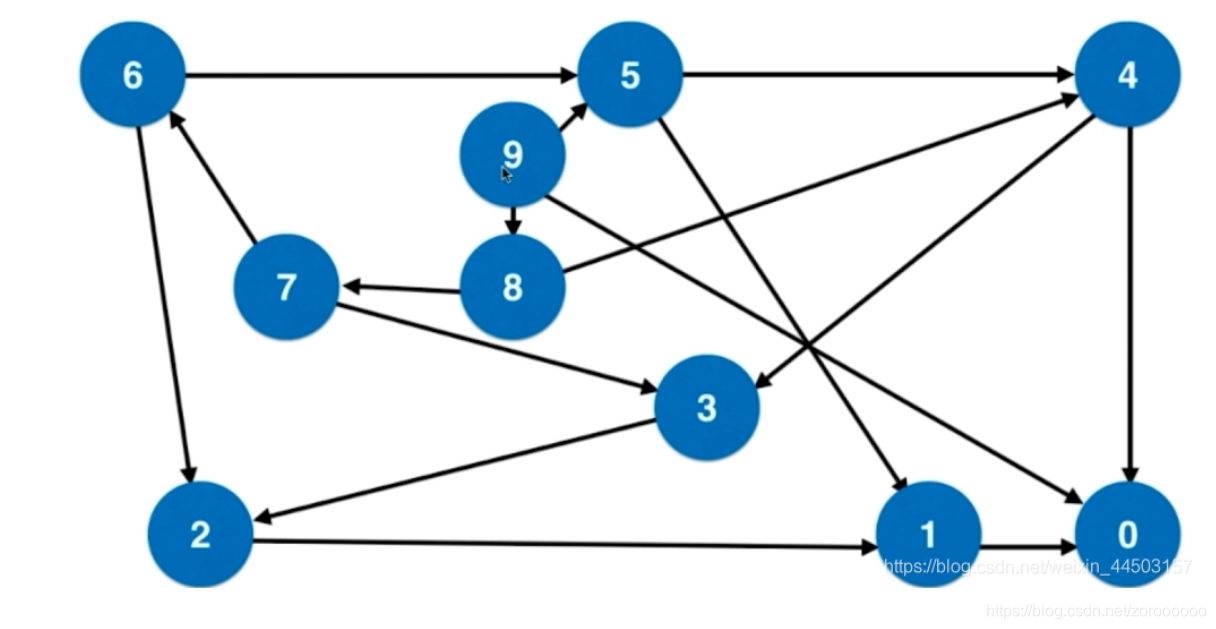
方法2.转换思想，转换成为图论的问题：

1. 从n到0，每个数字表示一个节点
2. 如果两个数字，相差一个平方节点，则连接一条边；得到无权图；
3. 问题转换为求无权图中n到0的最短路径
   
   

class Solution {
public:
        //使用BFS层级遍历,结合上图看更清楚
    int numSquares(int n) {
        queue<int> q;//定义q存储每次产生的下一个数
        q.push(n);
        vector<int> visited(n+1,0);//遍历过的值
        int step = 0;  //定义层数也就是最少步数，BFS用来求最少距离
        while(!q.empty()){
            step++;//循环一次 步数加1
            int size = q.size();
            for(int i = 0;i<size;i++){
                //将同一层的元素取出并把下一层产生的元素存储进去
                auto x = q.front();
                q.pop();
                for(int y = sqrt(x);y>=0;y--){//看图。很清楚
                    int t = x-y*y;
                    if(t==0) return step;
                    if(visited[t]!=1){
                        q.push(t);
                        visited[t] = 1;
                    }
                }
            }
        }
        return step;
    }
};

【127. 单词接龙】

所以这道题要解决两个问题：
1. 图中的线是如何连在一起的
2. 起点和终点的最短路径长度

首先题目中并没有给出点与点之间的连线，而是要我们自己去连，条件是字符只能差一个，所以判断点与点之间的关系，要自己判断是不是差一个字符，如果差一个字符，那就是有链接。

然后就是求起点和终点的最短路径长度，这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。

本题如果用深搜，会非常麻烦。

另外需要有一个注意点：

1. 本题是一个无向图，需要用标记位，标记着节点是否走过，否则就会死循环！
2. 本题给出集合是数组型的，可以转成set结构，查找更快一些

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        // 将vector转成unordered_set，提高查询速度
        unordered_set<string> wordSet(wordList.begin(), wordList.end());
        // 如果endWord没有在wordSet出现，直接返回0
        if (wordSet.find(endWord) == wordSet.end()) return 0;
        // 记录word是否访问过
        unordered_map<string, int> visitMap; // <word, 查询到这个word路径长度>
        // 初始化队列
        queue<string> que;
        que.push(beginWord);
        // 初始化visitMap
        visitMap.insert(pair<string, int>(beginWord, 1));

        while(!que.empty()) {
            string word = que.front();
            que.pop();
            int path = visitMap[word]; // 这个word的路径长度
            for (int i = 0; i < word.size(); i++) {
                string newWord = word; // 用一个新单词替换word，因为每次置换一个字母
                for (int j = 0 ; j < 26; j++) {
                    newWord[i] = j + 'a';
                    if (newWord == endWord) return path + 1; // 找到了end，返回path+1
                    // wordSet出现了newWord，并且newWord没有被访问过
                    if (wordSet.find(newWord) != wordSet.end()
                            && visitMap.find(newWord) == visitMap.end()) {
                        // 添加访问信息
                        visitMap.insert(pair<string, int>(newWord, path + 1));
                        que.push(newWord);
                    }
                }
            }
        }
        return 0;
    }
};

3.3、优先队列 ：堆

——优先队列问题，通常涉及到堆；

——堆的实现，可以使用数组模拟一棵树；常用！

【347. 前 K 个高频元素】 要求O小于O(nlogn)

——k个优先队列O（nlogk）

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        //统计频率,放入map，<数值，频率>
        unordered_map<int,int> mp;
        for(auto &i:nums){mp[i]++;}
        //优先队列,注意pq的first是频率。因为是根据first来比较的
        priority_queue<pii,vector<pii>,greater<pii>> pq;
        for(auto &it:mp){
            if(pq.size()==k){
                if(it.second > pq.top().first){//注意这里的it.second不是->
                    pq.pop();
                    pq.push({it.second,it.first});
                }
            }
            else{pq.push({it.second,it.first});}
        }
        vector<int> res;
        while(!pq.empty()){
            res.push_back(pq.top().second);
            pq.pop();
        }
        return res;
    }
};

【待做】【23. 合并K个升序链表】