[数据结构与算法]二叉树的性质

二叉树的性质

1.二叉树的性质一

在二叉树的第 $i$ 层至多有 $2^{i?1}$个结点($i\ge 1$)

2.二叉树的性质二

深度为k的二叉树至多有 $2^k?1$ 个结点（$k\ge 1$）

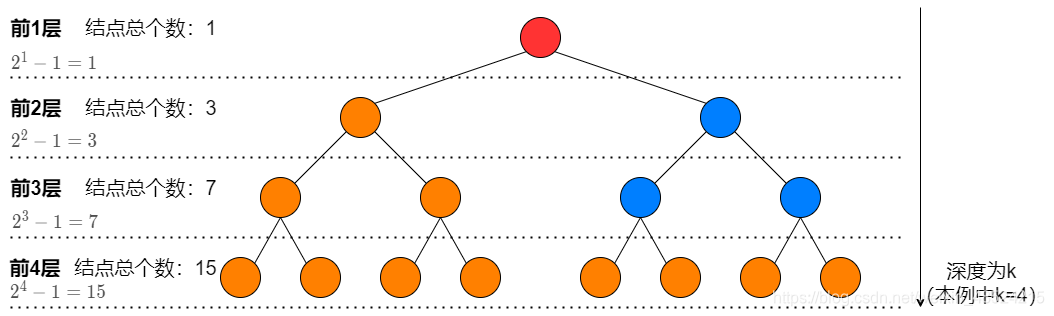
3.二叉树的性质三

对任何一棵二叉树T，如果其叶子结点数为 $n_0$ ，度为 $2$ 的结点数为 $n_2$，则 $n_0=n_2+1$

设 $n_0$ 为叶子，$n_1$ 为度是 1 的结点数，则树T的结点总数 $n=n_0+n_1+n_2$
观察二叉树后得：
$$树的分支总数=总结点数(n)?1$$
例如：3个结点2个分支，4个结点3个分支

二叉树由度数为2和1的结点组成，所以
$$树的分支总数=2n_2+n_1$$
得到式 $n?1=2n_2+n_1$
$$\{\begin{array}{r}n?1=2n_2+n_1\\ n=n_0+n_1+n_2\end{array}$$
解得：
$$n_0=n_2+1$$
例如上图中：$n_0=5$（G、F、H、I、J三个结点）$n_2=4$

4.二叉树的性质四

具有 n 个结点的完全二叉树的深度为 $?lo{g}_{2}n?+1$ （$?x?$表示不大于x的最大整数）

满二叉树总结点数一定为：$n=2^k?1$
倒推出满二叉树的深度为：$k=lo{g}_2(n+1)$

对于完全二叉树而言：
k-1层满二叉树的结点数 $2^{k?1}?1<$ 结点数（n） $<$ 同深度的满二叉树的结点数 $2^k?1$

5.二叉树的性质五

如果对一棵有 n 个结点的完全二叉树（其深度为 $?lo{g}_{2}n?+1$）的结点按层序编号（从上到下，从左到右，依次增大），对任一结点 i ($1\le i\le n$)有：
如果 $i=1$，则结点 $i$ 是二叉树的根，无双亲
如果 $i>1$，则其双亲是结点 $?\frac{i}{2}?$
如果 $2i>n$，则结点 $i$ 无左孩子（即为叶子）；否则其左孩子是结点 $2i$
如果 $2i+1>n$，则结点 $i$ 无右孩子；否则其右孩子是结点 $2i+1$

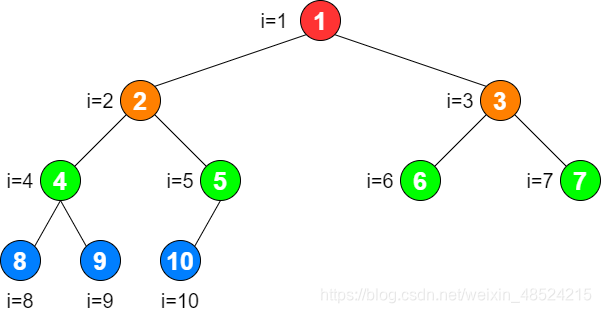
例如上图：
$i=1$，该结点无双亲
$i=2$，其双亲是结点 $?2/2?=1$
$i=5$，$2i+1=10+1=11>n=10$，所以该结点无右孩子
$i=6$，$2i=12>n=10$，所以该结点无左孩子