什么是动态规划
运筹学的一种最优化的方法
动态规划解决那类问题
动态规划问题的一般形式就是求最值,而求最值的最核心问题就是穷举所有可行答案找最值;穷举所有可行答案就需要找到状态转移方程式,通过状态转移方程才能找到正确地穷举;在穷举的过程难免会出现重叠子问题,此时就需要备忘录或者dp table来优化穷举的过程;而且动态规划问题一定具体最优子结构,这样才能通过子问题的最值找到原问题的最值。常见动态规划问题求最长递增子序列、最小编辑距离等
动态规划的三要素
重叠子问题、最优子结构、状态转移方程式
重叠子问题
通过斐波那契数列来说明重叠子问题问题
算法时间复杂度:子问题个数乘以一个子问题需要的时间
递归解法
func fib(n int) int {
if n <= 0 {
return 0
}
if n == 1 || n == 2 {
return 1
}
return fib(n-1) + fib(n-2)
}递归树如下图,子问题个数为递归树中所有节点的总数O() ,子问题时间复杂度为O(1),所以递归实现的时间复杂度为O(
)?。通过递归树可以发现在递归的过程存在大量的重复计算浪费了巨大的时间,这就是重叠子问题问题。解决该问题可以使用下面的带备忘录的递归算法实现
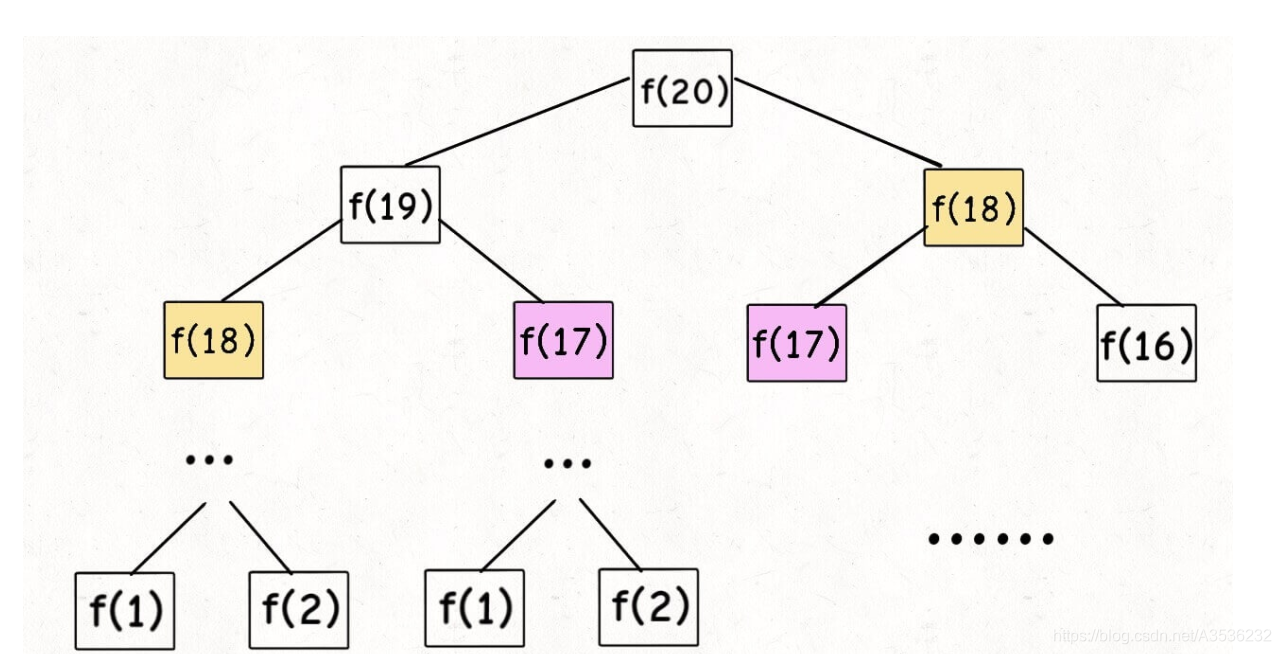
?带备忘录的递归算法实现,自顶向下
func fib(n int) int {
if n < 1 {
return 0
}
tmp := make([]int, n)
return help(tmp, n)
}
func help(tmp []int, n int) int {
if n == 1 || n == 2 {
return 1
}
if tmp[n-1] != 0 {
return tmp[n-1]
}
tmp[n-1] = help(tmp, n-1) + help(tmp, n-2)
return tmp[n-1]
}动态规划方式解决,自底向上
func fib(n int) int {
if n < 1 {
return 0
}
if n == 1 || n == 2 {
return 1
}
pre, cur := 1, 1
for i := 3; i <= n; i++ {
sum := pre + cur
pre = cur
cur = sum
}
return cur
}