红黑树
1. 特点
《算法》中对红黑树的定义(针对的是线的颜色):
- 红色的线永远是左侧链接。(强行的规定)
- 没有一个节点同时链了两条红色的线。(也就是没有4-node)
- 任何从根到叶子节点的路径上有相同颜色的黑线。(黑线节点完美平衡)
红黑树合并为2-3查找树:
右侧有红色的线,要先通过旋转变为左侧的线,再合并:
合并的过程实质上是把红色的线拉成平的,就能清晰的看出2-3树和红黑树的关系
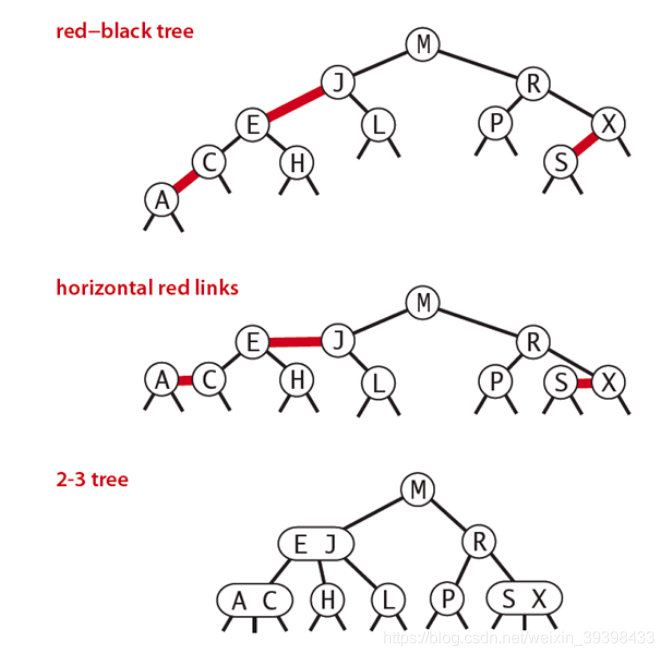
我们会把红线的红色信息放在子节点上,让子节点记录红色
红黑树中的红节点是什么意思? 根据上述内容用自己的话表达
2. 操作
2.1 旋转
按照下图书写左旋和右旋函数
(注意书写q,p,b的关系)
(还要注意红线是如何转移的)
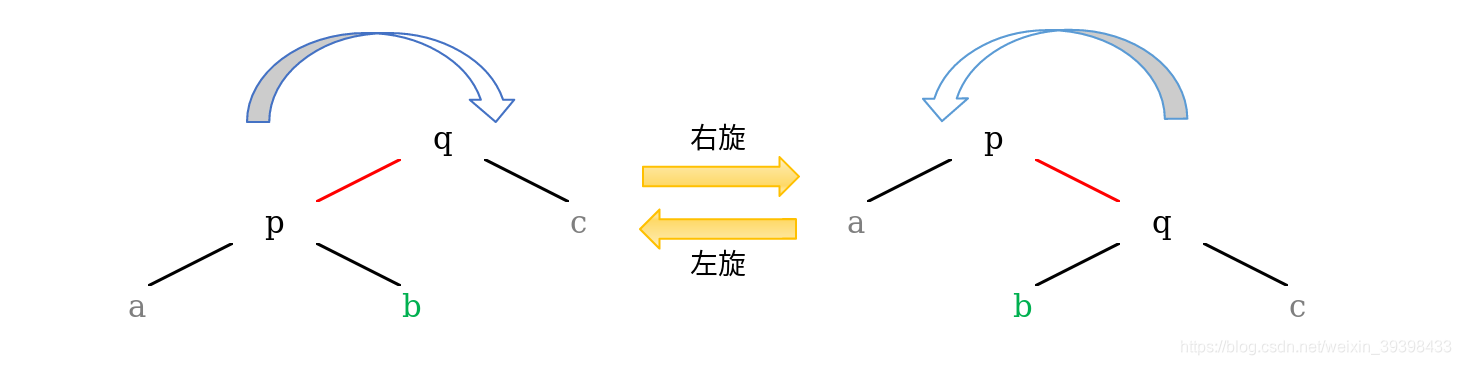
对应上图写出左旋和右旋操作
#include <iostream>
using namespace std;
enum COLOR{RED,BLACK}; // 枚举红黑两种颜色
template <typename T>
class _Node{
public:
T val;
COLOR color = BLACK; // 定义颜色
_Node* left;
_Node* right;
_Node(const T& val):val(val),left(nullptr),right(nullptr){}
_Node(const T& val,_Node* left,_Node* right):val(val),left(left),right(right){}
};
typedef _Node<int> Node;
// 右旋操作
Node* RotateRight(Node* root){
Node* q = root;
Node* p = root->left;
Node* b = p->right;
/* 转后 */
p->right = q;
q->left = b;
/* 颜色变换 */
p->color = q->color;
q->color = RED;
return p;
}
// 左旋操作
Node* RotateLeft(Node* root){
Node* p = root;
Node* q = p->right;
Node* b = q->left;
/* 转后 */
q->left = p;
p->right = b;
/* 颜色变换 */
q->color = p->color;
p->color = RED;
return q;
}
// 画一下树
void Preorder(Node* root){
if(nullptr == root) return;
if(root->left){
cout << root->val << "--" << root->left->val;
if(root->left->color == RED) cout << "[color=red]";
cout << endl;
}
if(root->right){
cout << root->val << "--" << root->right->val;
if(root->right->color == RED) cout << "[color=red]";
cout << endl;
}
Preorder(root->left);
Preorder(root->right);
}
int main(){
// 插入顺序为1,2,3
Node a(1);
Node b(2);
Node c(3);
c.color = RED;
a.right = &b;
b.right = &c;
Preorder(&a);
a.right = RotateLeft(&b); // 以2为基准左旋
Preorder(&a);
a.right = RotateRight(&c); // 再以3为基准右旋,又旋转回去了
Preorder(&a);
}
结果为:
// 原树型
1--2
2--3[color=red]
// 以2为基准左旋
1--3
3--2[color=red]
// 再以3为基准右旋
1--2
2--3[color=red]
对应树的变换如图所示:
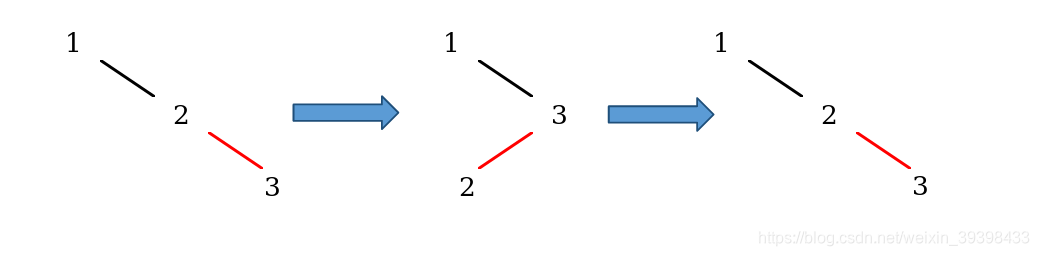
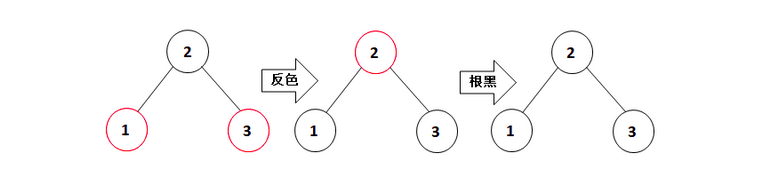
2.2 颜色翻转
颜色翻转:两个子节点由红色变为黑色,父节点由黑色变为红色,或者反过来
// 不为空且为红色
bool IsRed(Node* root){
return nullptr!=root && root->color==RED;
}
// 做颜色翻转
Node* FlipColor(Node* root){
if(IsRed(root->left) && IsRed(root->right)){ // 左子节点和右子节点都是红色,进行颜色翻转
root->left->color = BLACK;
root->right->color = BLACK;
root->color = RED;
}
return root;
}
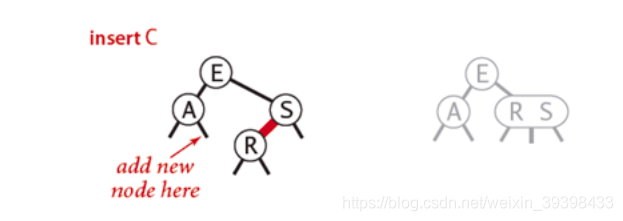
2.3 插入
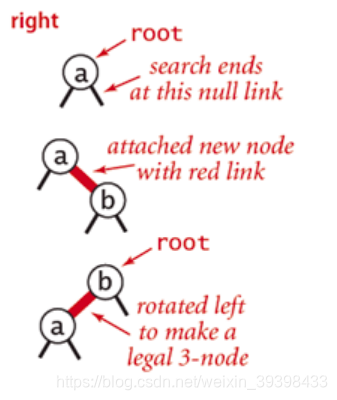
往一个2-node节点底部插入新的节点
按照BST遍历,新插入的节点标记为红色
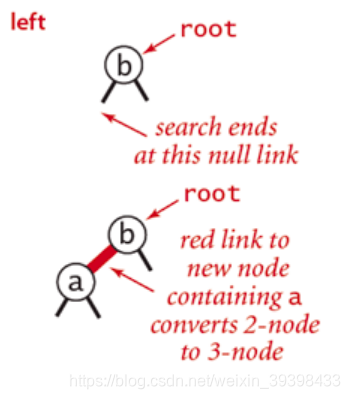
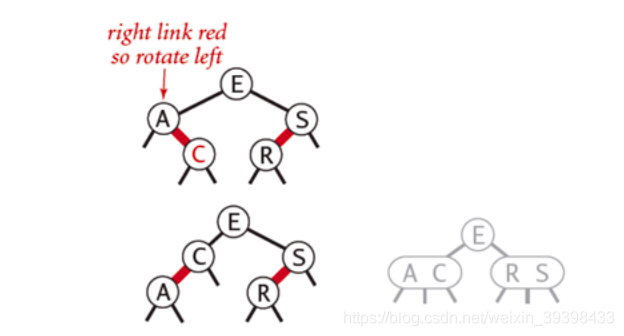
如果新插入的节点在父节点的右子节点,则需要进行左旋操作
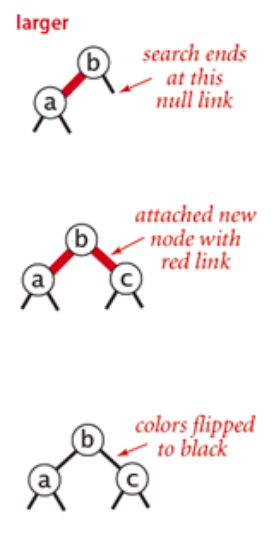
往一个3-node节点底部插入新的节点
-
插入的节点比现有的两个节点都大,新插入的节点连接到右边子树上,颜色反转
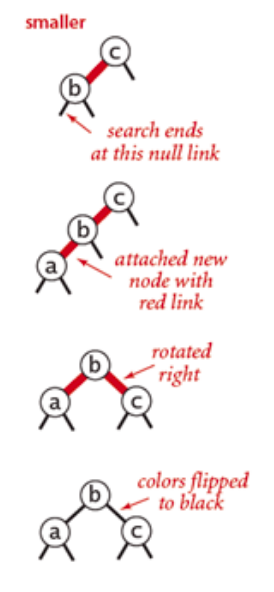
-
插入的节点比现有的两个节点都小,新插入的节点连接到最左侧,以c为基准右旋,颜色反转
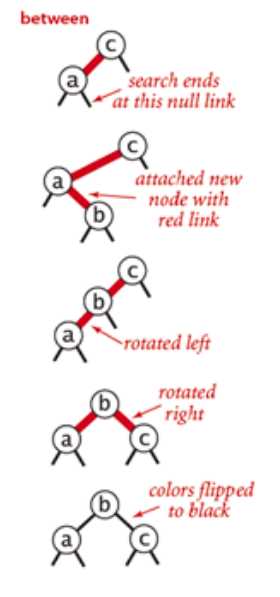
-
插入的节点的值位于两个节点之间,新节点插入到左侧节点的右子节点,先以a为基准左旋,再以c为基准右旋,颜色反转
找到规律并获得插入方法
由此可找到规律,对下面的操作按顺序依次执行,就可以完成红黑树的插入:
- 如果右子节点为红,左子节点不为红,要做一次左旋;
- 如果左子节点为红,左子节点的左子节点也为红,要做一次右旋;
- 如果左子节点为红,右子节点也为红,要做颜色翻转。
// 形成正规的红黑树
Node* Blance(Node* root){
if(IsRed(root->right) && !IsRed(root->left)) root = RotateLeft(root);
if(IsRed(root->left) && IsRed(root->left->left)) root = RotateRight(root);
if(IsRed(root->left) && IsRed(root->right)) root = FlipColor(root);
return root;
}
综合应用:
依次按顺序插入1,2,3,4,5,6并通过平衡查看生成的红黑树
#include <iostream>
using namespace std;
enum COLOR{RED,BLACK}; // 枚举红黑两种颜色
template <typename T>
class _Node{
public:
T val;
COLOR color = RED; // 定义颜色,默认为红色
_Node* left;
_Node* right;
_Node(const T& val):val(val),left(nullptr),right(nullptr){}
_Node(const T& val,_Node* left,_Node* right):val(val),left(left),right(right){}
};
template <typename T>
// 查找、添加、删除
class RBTree{
typedef _Node<T> Node;
Node* m_root = nullptr;
public:
// 查找
bool Search(const T& val){
return Search(m_root,val);
}
bool Search(Node* root,const T& val){
if(nullptr == root) return false;
if(root->val == val) return true;
if(root->val < val){
return Search(root->right,val);
}else{
return Search(root->left,val);
}
}
// 插入
void Insert(const T& val){
if(Search(val)) return;
m_root = Insert(m_root,val);
m_root->color = BLACK; // 保证是根是黑色
}
Node* Insert(Node* root,const T& val){
if(nullptr == root) return new Node(val);
if(root->val > val){
root->left = Insert(root->left,val);
}else{
root->right = Insert(root->right,val);
}
return Balance(root); // 插入完后要做一次平衡处理
}
// 右旋操作
Node* RotateRight(Node* root){
Node* q = root;
Node* p = root->left;
Node* b = p->right;
/* 转后 */
p->right = q;
q->left = b;
/* 颜色变换 */
p->color = q->color;
q->color = RED;
return p;
}
// 左旋操作
Node* RotateLeft(Node* root){
Node* p = root;
Node* q = p->right;
Node* b = q->left;
/* 转后 */
q->left = p;
p->right = b;
/* 颜色变换 */
q->color = p->color;
p->color = RED;
return q;
}
// 不为空且为红色
bool IsRed(Node* root){
return nullptr!=root && root->color==RED;
}
// 做颜色翻转
Node* FlipColor(Node* root){
if(IsRed(root->left) && IsRed(root->right)){ // 左子节点和右子节点都是红色,进行颜色翻转
root->left->color = BLACK;
root->right->color = BLACK;
root->color = RED;
}
return root;
}
// 外部调用
void Print(){
Preorder(m_root);
}
// 画一下树
void Preorder(Node* root){
if(nullptr == root) return;
if(root->left){
cout << root->val << "--" << root->left->val;
if(root->left->color == RED) cout << "[color=red]";
cout << endl;
}
if(root->right){
cout << root->val << "--" << root->right->val;
if(root->right->color == RED) cout << "[color=red]";
cout << endl;
}
Preorder(root->left);
Preorder(root->right);
}
// 形成正规的红黑树
Node* Balance(Node* root){
if(IsRed(root->right) && !IsRed(root->left)) root = RotateLeft(root);
if(IsRed(root->left) && IsRed(root->left->left)) root = RotateRight(root);
if(IsRed(root->left) && IsRed(root->right)) root = FlipColor(root);
return root;
}
};
int main(){
RBTree<int> intbst;
int n;
while(cin >> n){
intbst.Insert(n);
}
intbst.Print();
}
结果为:
1 2 3 4 5 6
4--2[color=red]
4--6
2--1
2--3
6--5[color=red]
对应红黑树的图:
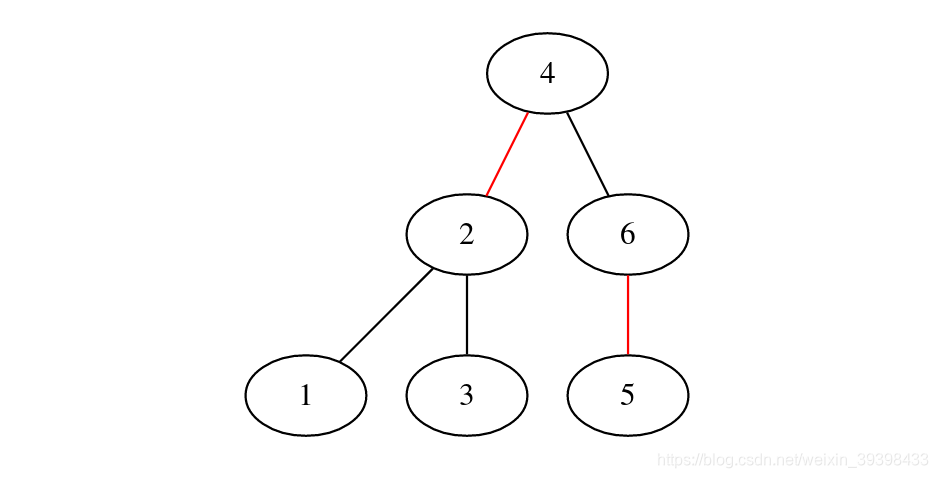
2.4 删除
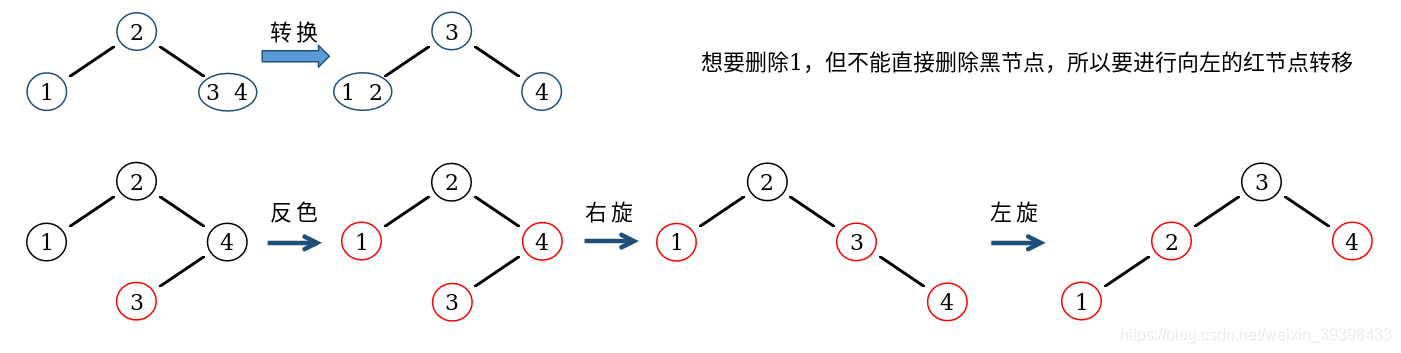
为了保证删除节点后该树依然满足红黑树,删除时不能删除黑节点,只能删除红节点,所以需要进行红节点转移的操作
红节点向左转移:
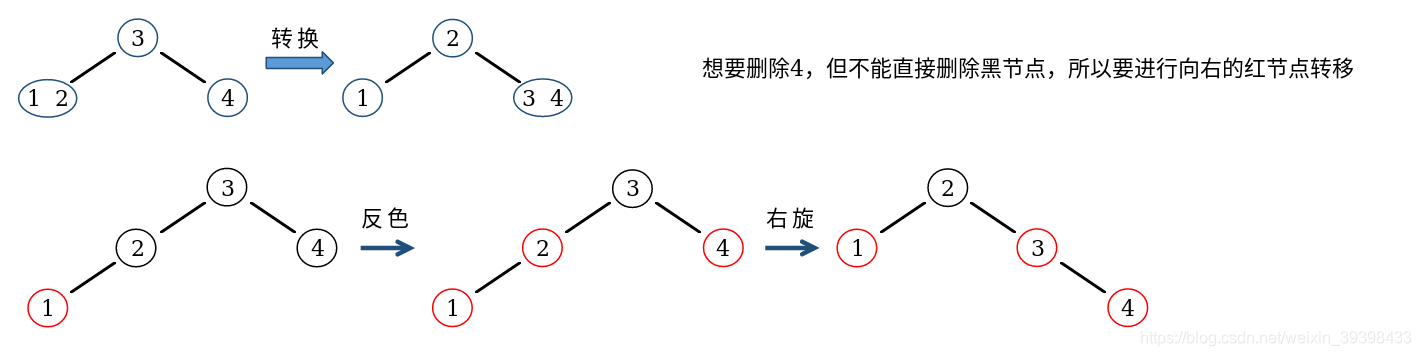
红节点向右转移:
这里的颜色翻转: 父节点由红色变为黑色,两个子节点由黑色变为红色
对应到具体函数中,可写为:
// 不为空且为红色
bool IsRed(Node* root){
return nullptr!=root && root->color==RED;
}
// 做颜色翻转
Node* FlipColor(Node* root){
if(IsRed(root->left) && IsRed(root->right)){ // 左子节点和右子节点都是红色,进行颜色翻转
root->left->color = BLACK;
root->right->color = BLACK;
root->color = RED;
}else if(!IsRed(root->left) && !IsRed(root->right)){ // 左子节点和右子节点都是黑色,进行颜色翻转
root->left->color = RED;
root->right->color = RED;
root->color = BLACK;
}
return root;
}
// 红节点向左转移
Node* MoveRedLeft(Node* root){
root = FlipColor(root); // 根节点反色
if(IsRed(root->right->left)){ // 如果右子节点的左子节点为红
root->right = RotateRight(root->right); // 先以右子节点为基准右旋
root = RotateLeft(root); // 再以根节点为基准左旋
}
return root;
}
// 红节点向右转移
Node* MoveRedRight(Node* root){
root = FlipColor(root); // 根节点反色
if(IsRed(root->left->left)){ // 如果左子节点的左子节点为红
root = RotateRight(root); // 以根节点为基准右旋
}
return root;
}
综合应用:
对已经生成的红黑树进行手动删除,看看删除节点前后红黑树的变化
注意删除部分的操作
#include <iostream>
using namespace std;
enum COLOR{RED,BLACK}; // 枚举红黑两种颜色
template <typename T>
class _Node{
public:
T val;
COLOR color = RED; // 定义颜色,默认为红色
_Node* left;
_Node* right;
_Node(const T& val):val(val),left(nullptr),right(nullptr){}
_Node(const T& val,_Node* left,_Node* right):val(val),left(left),right(right){}
};
template <typename T>
// 查找、添加、删除
class RBTree{
typedef _Node<T> Node;
Node* m_root = nullptr;
public:
// 查找
bool Search(const T& val){
return Search(m_root,val);
}
bool Search(Node* root,const T& val){
if(nullptr == root) return false;
if(root->val == val) return true;
if(root->val < val){
return Search(root->right,val);
}else{
return Search(root->left,val);
}
}
// 插入
void Insert(const T& val){
if(Search(val)) return;
m_root = Insert(m_root,val);
m_root->color = BLACK; // 保证是根是黑色
}
Node* Insert(Node* root,const T& val){
if(nullptr == root) return new Node(val);
if(root->val > val){
root->left = Insert(root->left,val);
}else{
root->right = Insert(root->right,val);
}
return Balance(root); // 插入完后要做一次平衡处理
}
// 删除
void Remove(const T& val){
m_root->color = RED;
m_root = Remove(m_root,val);
if(nullptr != m_root) m_root->color = BLACK;
}
Node* Remove(Node* root,const T& val){
if(nullptr == root) return nullptr;
if(root->val > val){ // 删除左子树的值,尝试向右子树借一下
if(!IsRed(root->left) && !IsRed(root->left->left)) root = MoveRedLeft(root); // 如果左子节点为黑,左子节点的左子节点为黑,则红节点向左转移
root->left = Remove(root->left,val);
}else if(root->val < val){ // 删除右子树的值,尝试想左子树借一下
if(IsRed(root->left)) root = RotateRight(root); // 如果左子节点为红,先右旋
if(!IsRed(root->right) && !IsRed(root->right->left)) root = MoveRedRight(root); // 如果右子节点为黑,右子节点的左子节点为黑,则红节点向右转移
root->right = Remove(root->right,val);
}else if(root->val == val){ // 删除当前值
if(nullptr == root->left && nullptr == root->right) {delete root; return nullptr;} // 如果是叶子节点,可以直接删除
if(nullptr == root->right){ // 只有左子树
/* 先尝试借一下 */
if(!IsRed(root->left) && !IsRed(root->left->left)) root = MoveRedLeft(root);
if(val == root->val){ // 判断是否借到
/* 如果没借到,左子树找最大值替换 */
T maxVal = Maximun(root->left);
root->val = maxVal;
root->left = Remove(root->left,maxVal);
}
}else{ // 有右子树
/* 先尝试借一下 */
if(IsRed(root->left)) root = RotateRight(root);
if(!IsRed(root->right) && !IsRed(root->right->left)) root = MoveRedRight(root);
if(val == root->val){ // 判断是否借到
/* 如果没借到,右子树找最小值替换 */
T minval = Minimun(root->right);
root->val = minval;
root->right = Remove(root->right,minval);
}else{
root->right = Remove(root->right,val); // 如果借到了就继续找
}
}
}
return Balance(root); // 删除完后要做一次平衡处理
}
// 找整个树的最小值
T Minimun(Node* root){
if(nullptr == root) throw runtime_error("root is null");
while(nullptr != root->left) root = root->left;
return root->val;
}
// 找整个树的最大值
T Maximun(Node* root){
if(nullptr == root) throw runtime_error("root is null");
while(nullptr != root->right) root = root->right;
return root->val;
}
// 右旋操作
Node* RotateRight(Node* root){
Node* q = root;
Node* p = root->left;
Node* b = p->right;
/* 转后 */
p->right = q;
q->left = b;
/* 颜色变换 */
p->color = q->color;
q->color = RED;
return p;
}
// 左旋操作
Node* RotateLeft(Node* root){
Node* p = root;
Node* q = p->right;
Node* b = q->left;
/* 转后 */
q->left = p;
p->right = b;
/* 颜色变换 */
q->color = p->color;
p->color = RED;
return q;
}
// 不为空且为红色
bool IsRed(Node* root){
return nullptr!=root && root->color==RED;
}
// 做颜色翻转
Node* FlipColor(Node* root){
if(IsRed(root->left) && IsRed(root->right)){ // 左子节点和右子节点都是红色,进行颜色翻转
root->left->color = BLACK;
root->right->color = BLACK;
root->color = RED;
}else if(!IsRed(root->left) && !IsRed(root->right)){ // 左子节点和右子节点都是黑色,进行颜色翻转
root->left->color = RED;
root->right->color = RED;
root->color = BLACK;
}
return root;
}
// 红节点向左转移
Node* MoveRedLeft(Node* root){
root = FlipColor(root); // 根节点反色
if(IsRed(root->right->left)){ // 如果右子节点的左子节点为红
root->right = RotateRight(root->right); // 先以右子节点为基准右旋
root = RotateLeft(root); // 再以根节点为基准左旋
}
return root;
}
// 红节点向右转移
Node* MoveRedRight(Node* root){
root = FlipColor(root); // 根节点反色
if(IsRed(root->left->left)){ // 如果左子节点的左子节点为红
root = RotateRight(root); // 以根节点为基准右旋
}
return root;
}
// 外部调用
void Print(){
if(nullptr == m_root){
cout << "null tree" << endl;
}else if(nullptr == m_root->right && nullptr == m_root->left){
cout << m_root->val << endl;
}else{
Preorder(m_root);
}
}
// 画一下树
void Preorder(Node* root){
if(nullptr == root) return;
if(root->left){
cout << root->val << "--" << root->left->val;
if(root->left->color == RED) cout << "[color=red]";
cout << endl;
}
if(root->right){
cout << root->val << "--" << root->right->val;
if(root->right->color == RED) cout << "[color=red]";
cout << endl;
}
Preorder(root->left);
Preorder(root->right);
}
// 形成正规的红黑树
Node* Balance(Node* root){
if(IsRed(root->right) && !IsRed(root->left)) root = RotateLeft(root);
if(IsRed(root->left) && IsRed(root->left->left)) root = RotateRight(root);
if(IsRed(root->left) && IsRed(root->right)) root = FlipColor(root);
return root;
}
};
int main(){
RBTree<int> intbst;
int arr[] = {1,3,5,7,2,4,6};
for(auto n:arr){
intbst.Insert(n);
}
intbst.Print();
int n;
while(cin >> n){
intbst.Remove(n);
intbst.Print();
}
}
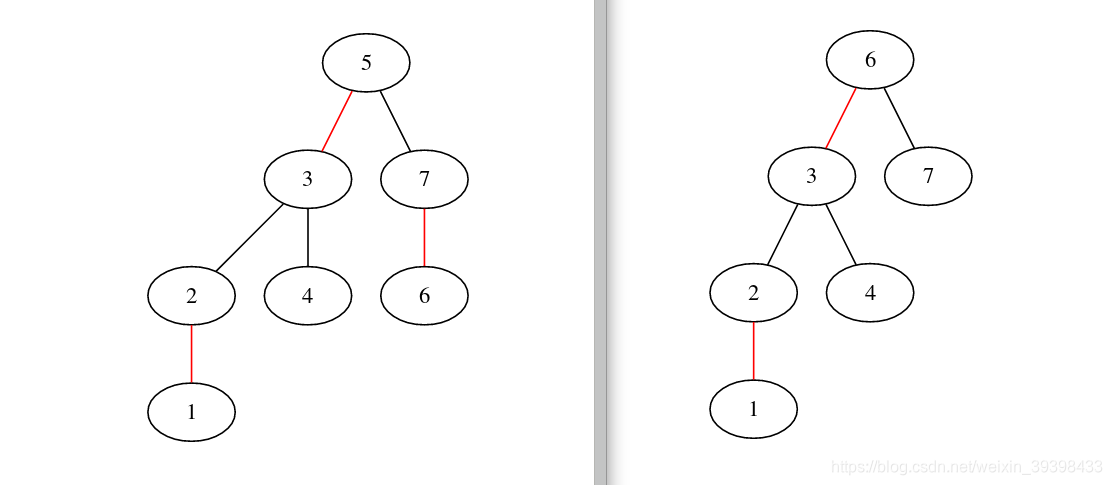
结果为:
5--3[color=red]
5--7
3--2
3--4
2--1[color=red]
7--6[color=red]
5
6--3[color=red]
6--7
3--2
3--4
2--1[color=red]
删除5节点前后对比图: