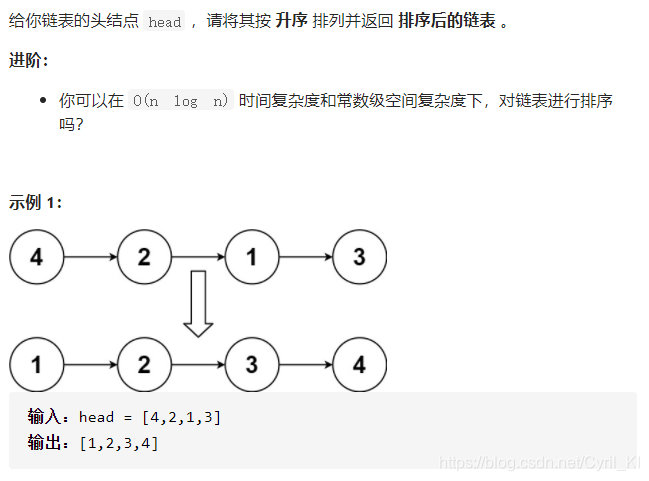
排序链表
方法一:
??暴力求解,先遍历保存所有节点值,排序后再创建新的链表。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
ListNode* ptr = head;
vector<int> res;
while(ptr) {
res.push_back(ptr->val);
ptr = ptr->next;
}
sort(res.begin(), res.end());
ListNode* lis = new ListNode(0);
ListNode* f = lis;
for(int x : res) {
ListNode* temp = new ListNode(x);
lis->next = temp;
lis = temp;
}
return f->next;
}
};
方法二:
??归并排序:参考官方题解。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
return sortList(head, nullptr);
}
ListNode* sortList(ListNode* head, ListNode* tail) {
if (head == nullptr) {
return head;
}
if (head->next == tail) {
head->next = nullptr;
return head;
}
ListNode* slow = head, *fast = head;
while (fast != tail) {
slow = slow->next;
fast = fast->next;
if (fast != tail) {
fast = fast->next;
}
}
ListNode* mid = slow;
return merge(sortList(head, mid), sortList(mid, tail));
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
乘积最大子数组

分析:
??遍历数组中的元素,并不断更新最大乘积。令imax表示以当前元素结尾的序列的最大乘积,imin为最小乘积。所以状态转移方程为:
imax = max(imax * x, x);
imin = min(imin * x, x);
??即有两种选择方式:乘上或者不乘上当前元素。
??如果当前元素x < 0,这个时候的最小值乘上x就会变成最大值,所以需要交换imin和imax。
代码:
class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
int imax = 1, imin = 1;
int res = INT_MIN;
for(int x : nums) {
if(x < 0) {
int t = imax;
imax = imin;
imin = t;
}
imax = max(imax * x, x);
imin = min(imin * x, x);
res = max(imax, res);
}
return res;
}
};
打家劫舍
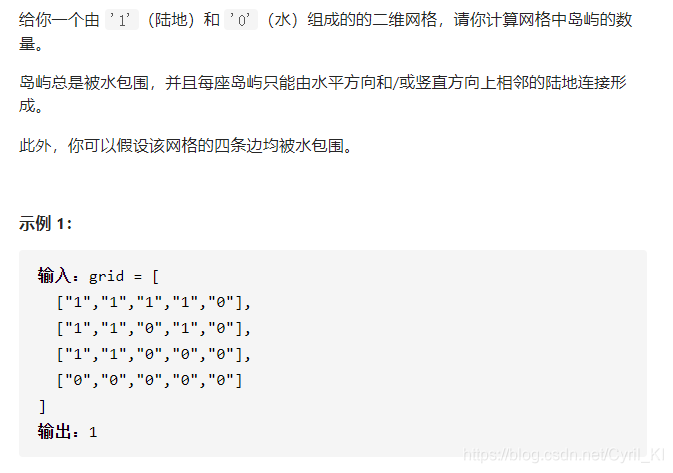
岛屿数量
分析:
??简单的dfs,遍历找到一个1,然后进行dfs直到访问完周围能够访问到的所有1,然后岛屿数+1。
代码:
class Solution {
private:
int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int m, n;
int res = 0;
vector<vector<int>> visited;
bool in(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}
public:
void dfs(vector<vector<char>>& grid, int x, int y) {
if(!in(x, y) || grid[x][y] != '1' || visited[x][y]) {
return;
}
visited[x][y] = 1;
for(int i = 0; i < 4; i++) {
int xx = x + dirs[i][0];
int yy = y + dirs[i][1];
dfs(grid, xx, yy);
}
}
int numIslands(vector<vector<char>>& grid) {
m = grid.size(), n = grid[0].size();
visited = vector<vector<int>>(m, vector<int>(n, 0));
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(grid[i][j] == '1' && !visited[i][j]) {
dfs(grid, i, j);
res++;
}
}
}
return res;
}
};
数组中的第K个最大元素

方法一:
??先排序再求解。
代码:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
sort(nums.begin(), nums.end(), greater<int>());
return nums[k - 1];
}
};
方法二:
??使用大根堆:先建堆,然后删除k - 1次堆顶元素,最后再返回堆顶元素即可。这里建议自己实现建堆、删除以及调整的代码。
代码:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, less<int>> que; //大根堆
for(int x : nums) {
que.push(x);
}
for(int i = 0; i < k - 1; i++) {
que.pop();
}
return que.top();
}
};
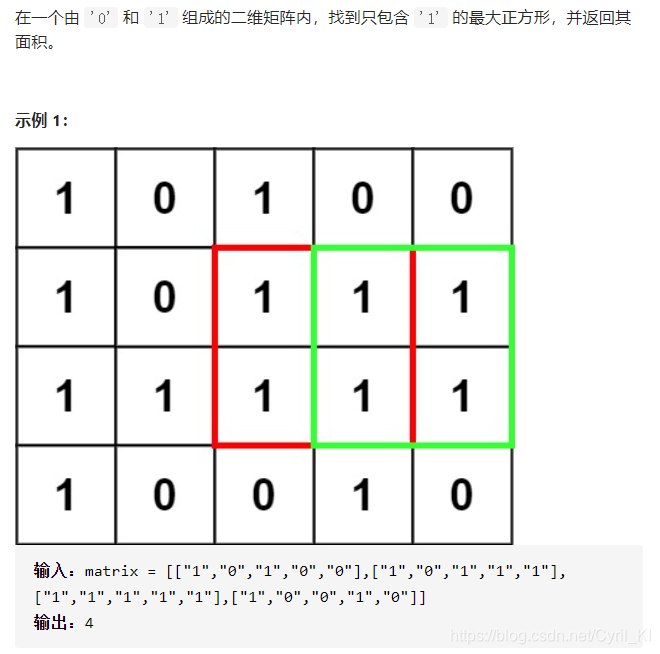
最大正方形
方法一:
??暴力求解:遍历矩阵,找到一个1,然后以当前位置作为正方形的左上角,不断扩张边长,求得面积最大值。
代码:
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int res = 0;
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
if(matrix[i][j] != '1') {
continue;
}
int x = i, y = j;
//依次增加行和列数
for(int k = 0; x + k < m && y + k < n; k++) {
bool flag = true;
for(int s = i; s <= i + k; s++) {
for(int t = j; t <= j + k; t++) {
if(matrix[s][t] != '1') {
flag = false;
break;
}
}
if(!flag) {
break;
}
}
if(flag) {
res = max(res, (k + 1) * (k + 1));
}
}
}
}
return res;
}
};
方法二:
??动态规划:设dp[i][j]表示以ij为右下角且满足条件的正方形边长的最大值。边界条件:第0行或者第0列的dp值为1。转移方程:如果当前位置为0,则dp只能为0,因为0不能包含在正方形里面;如果当前位置为1,则有:
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
??即当前的dp与其左边上边以及左上角的dp值有关,这个比较容易理解。
代码:
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
int res = 0;
//边界条件:
for(int i = 0; i < m; i++) {
if(matrix[i][0] == '1') {
res = 1;
dp[i][0] = 1;
}
}
for(int j = 0; j < n; j++) {
if(matrix[0][j] == '1') {
res = 1;
dp[0][j] = 1;
}
}
for(int i = 1; i < m; i++) {
for(int j = 1; j < n; j++) {
if(matrix[i][j] == '0') {
continue;
}
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
res = max(res, dp[i][j]);
}
}
return res * res;
}
};
二叉树的最近公共祖先
除自身以外数组的乘积
搜索二维矩阵 II
完全平方数

分析:
??这个题在前段时间的北邮CS夏令营机考中碰到了,当时四个题45分钟,没做出来这题。这个题可以采用动态规划来做:设dp[i]表示和为n的最小的完全平方数的个数。因为这里有n >= 1,所以有dp[0] = 0。转移方程:
res = min(res, dp[i - j * j]);(j∈[1, sqrt(i)])
dp[i] = res + 1;
??即:i与i - j * j相比,要加上一个j的平方,其完全平方数的个数要加上1。这里的j有很多个取值,我们遍历j然后取一个最小的答案即可。
代码:
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1);
for(int i = 1; i <= n; i++) {
int res = INT_MAX;
for(int j = 1; j * j <= i; j++) {
res = min(res, dp[i - j * j]);
}
dp[i] = res + 1;
}
return dp[n];
}
};