判断一个树是否为完全二叉树
1. 完全二叉树定义
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
一棵二叉树至多只有最下面的一层上的结点的度数可以小于2,并且最下层上的结点都集中在该层最左边的若干位置上,而在最后一层上,右边的若干结点缺失的二叉树,则此二叉树成为完全二叉树。

2. 如何判断?
根据定义,我们可以知道,完全二叉树的判断可以分为两个阶段
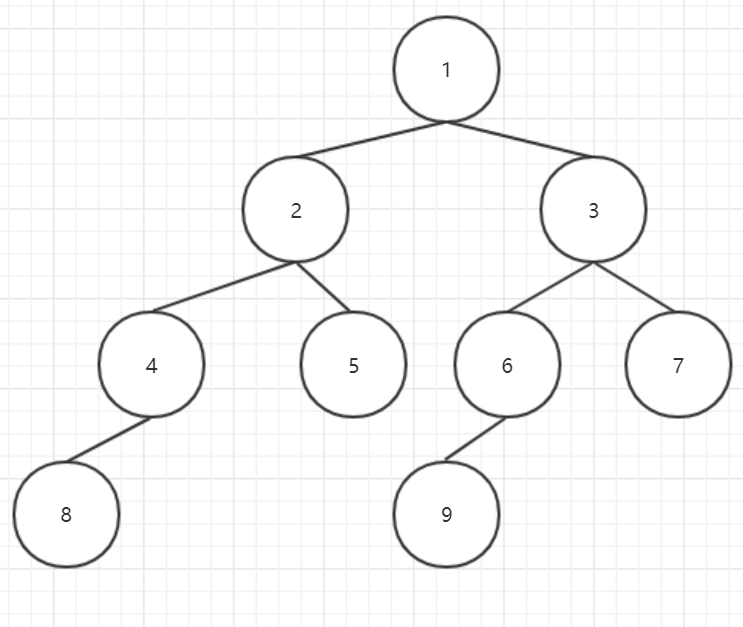
- 第一阶段(非叶节点)
- 当前节点不为空,其左右孩子均为空**(下图中的5号节点)**,继续判断其他节点
- 当前节点不为空,且其左右孩子也不为空**(下图中的2号节点)**,继续判断其他节点
- 当前节点不为空,且其左孩子不为空,右孩子为空**(下图中的4号节点)**,继续判断其他节点
- 当前节点不为空,左孩子为空,但其右孩子不为空**(下图中的6号节点)**(非完全二叉树),直接退出
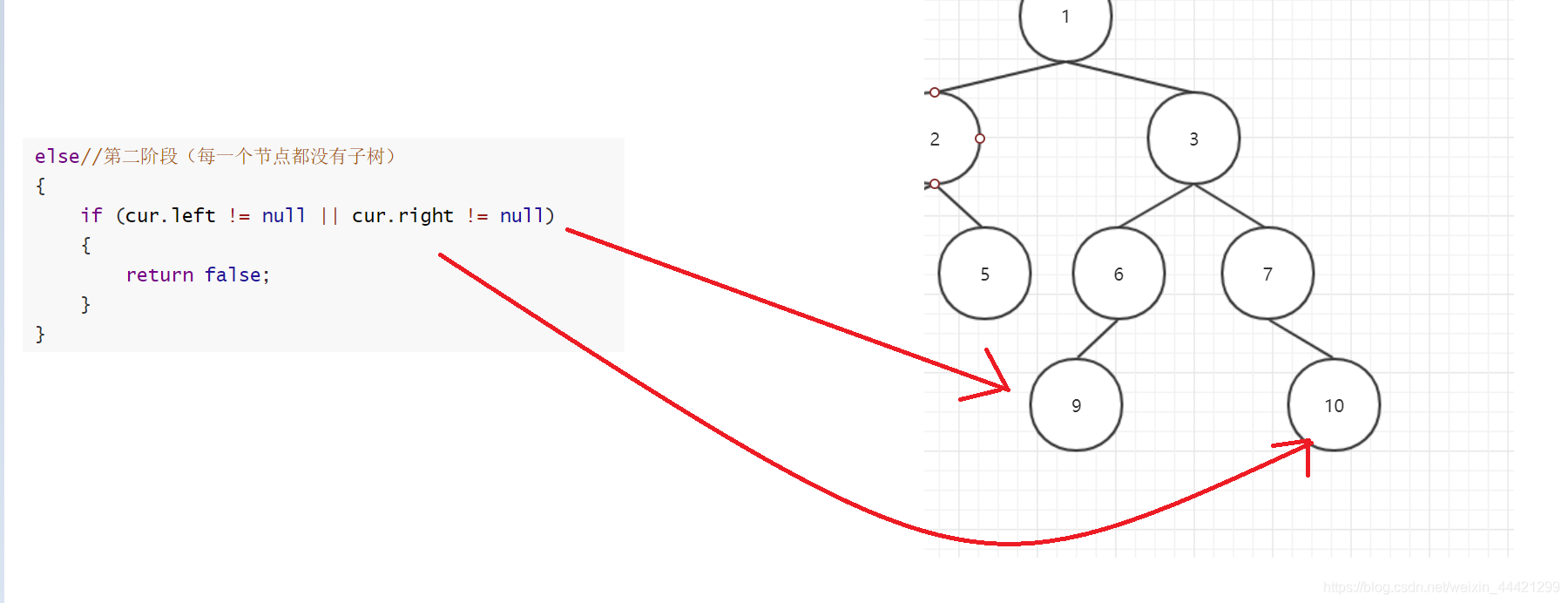
- 第二阶段(叶节点)
- 当前节点不为空,其左右孩子不同时为空**(下图中的5、7、8号节点)**(非完全二叉树),直接退出
综上,代码如下
public boolean isCompleteTree(TreeNode root)
{
//如果树为空,则直接返回错
if (root == null)
{
return false;
}
//如果树不为空:层序遍历二叉树
Queue<TreeNode> queue = new LinkedList<>();
//设置第二阶段(节点没有子树)标志位
boolean isSecondStep = false;
//首先把根节点加入
queue.offer(root);
//当队列不为空,循环遍历
while (!queue.isEmpty())
{
//将当前元素取出队列
TreeNode cur = queue.poll();
//判断是否满足完全二叉树
if (!isSecondStep) //第一阶段(所有节点有两个子树)
{
if (cur.left != null && cur.right != null )
{
//如果左右孩子均不为空,将其加入队列
queue.offer(cur.left);
queue.offer(cur.right);
}
else if (cur.left == null && cur.right != null)
{
//只有右子树没有左子树
return false;
}
else if (cur.left != null && cur.right == null)
{
//第一阶段中一个节点只有左子树没有右子树,开始进入第二阶段
isSecondStep = true;
queue.offer(cur.left);
}
else
{
//左右子树都为空,也要切换到第二阶段
isSecondStep = true;
}
}
else//第二阶段(每一个节点都没有子树)
{
if (cur.left != null || cur.right != null)
{
return false;
}
}
}
//整个树遍历结束仍未找到,说明是完全二叉树
return true;
}
3. 代码举例分析
第一阶段
3.1 情况1
? 如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列,如下图2号节点
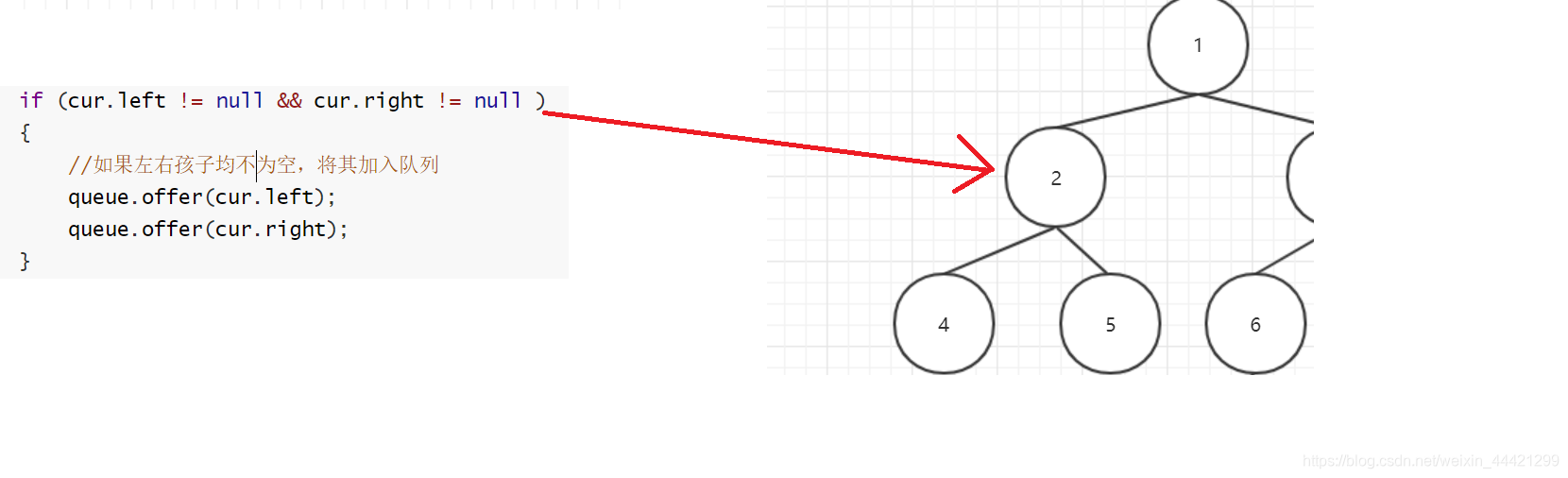
3.2 情况2
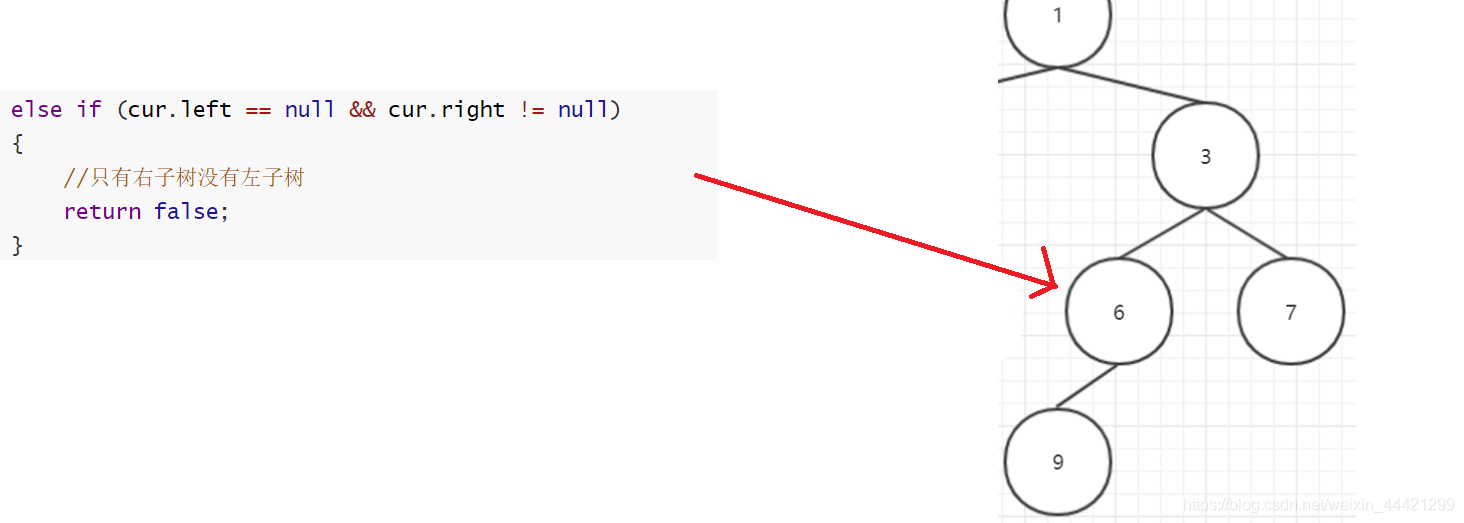
如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树,如下图的6号节点情况
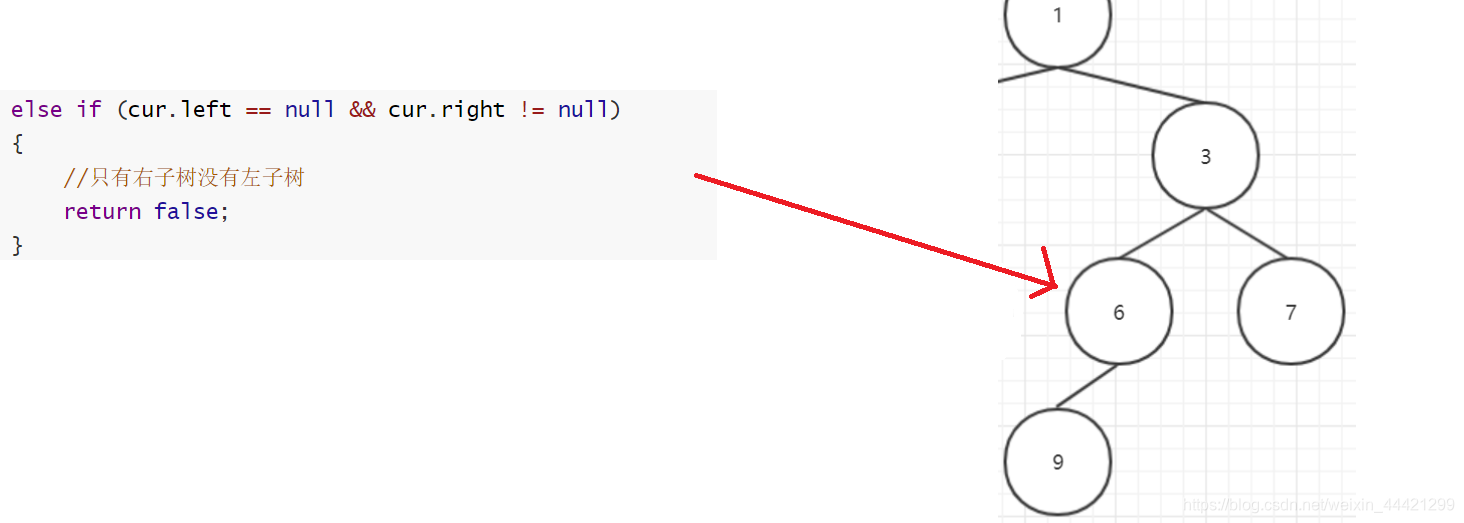
3.3 情况3
当出现只有左子树没有右子树,开始进入第二阶段,如图中的8号节点
3.4 情况4
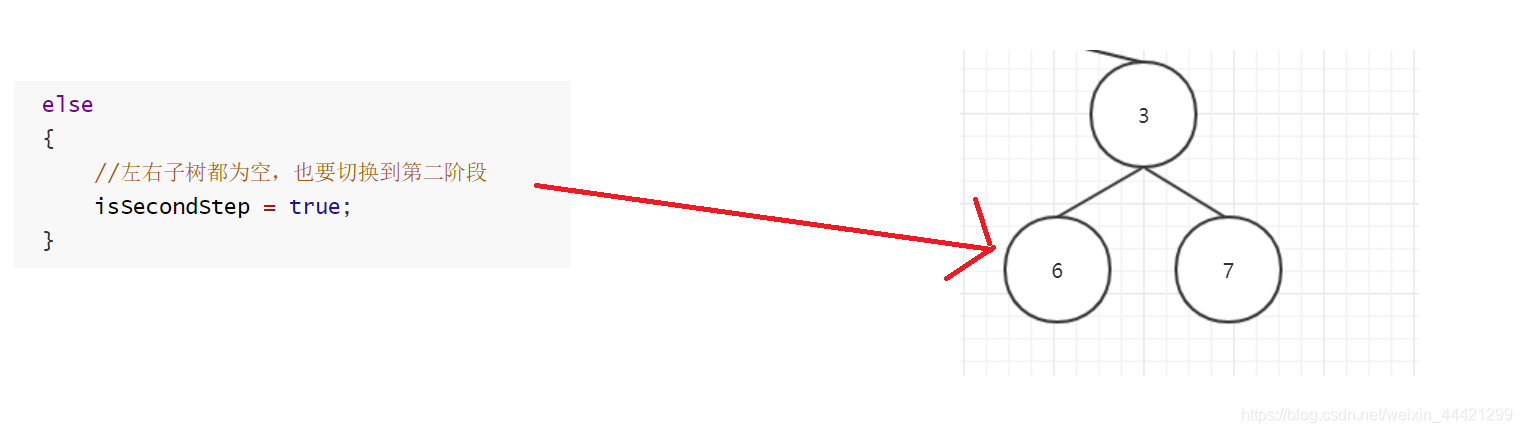
当出现左右子树均空,开始进入第二阶段,如图中的6号节点
第二阶段
3.5 情况1
当出现左右子有任意一方不为空,如图中的9、10号节点